Конспект открытого урока алгебры 9 класс по теме: «Числовая последовательность»

Конспект открытого урока алгебры  9 класс

по теме:

«Числовая  последовательность»

Цели урока:

- закрепить знание способов задания числовой последовательности;

- изучить свойства числовых последовательностей и научиться применять их в  

                                                                                  ходе выполнения упражнений;

     - развить логическое мышление учащихся;

     - проверить знания учащихся (самостоятельная работа в виде теста).

Оборудование: мультимедиапроектор, ПК, презентация, доска, мел, указка.

1. Организационный момент

«Числа управляют миром»,- говорили древнегреческие ученые. «Все есть число». Согласно их философскому мировоззрению, числа управляют не только мерой и весом, но также явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса. Так первым четырем числам – 1, 2, 3, 4 – приписывалось: 1 – означает огонь, 2 – землю, 3 – воду, 4 – воздух. Сумма этих чисел – число 10 – изображало весь мир. Но числа дают возможность самому человеку управлять миром.

Сегодня на уроке мы познакомимся с понятием «последовательность», узнаем, какими могут быть последовательности и рассмотрим способы задания последовательностей.

1. Устная работа.

 Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день?

Задача 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на 2. сколько бактерий будет в колонии, рожденной одной бактерией за 4 минуты?

(Слайд)

Для того чтобы ответить, на вопрос задачи нам необходимо было составить определенную числовую последовательность

Что бы дать определение  числовой последовательности и ответить на следующие вопросы обратимся к тексту учебника

3. Изучение нового материала.

Рассмотренные нами числовые ряды и есть примеры числовых последовательностей. Числа, образующие последовательность, называют соответственно первым, вторым, третьим, и т. д., n-ным членами последовательности.

Обозначают члены последовательности так а1; а2; а3; а4; … аn;

Последовательности могут быть конечными и бесконечными, возрастающими и убывающими. Задания для устной работы

1. Назовите в последовательности 1; 1/2; 1/3; 1/4; 1/5; … 1/n; 1/(n+1) члены а1; а4; а10; аn;

2. Является ли последовательность четырѐхзначных чисел конечной? (да)

3. Назовите еѐ первый и последний члены. (Ответ: 1000; 9999)

4. Является ли последовательностью запись чисел 2; 4; 7; 1; -21; -15; …? (нет, так как нельзя по первым шести членам обнаружить какую-нибудь закономерность) Существуют различные способы, которые позволяют задать последовательность. С помощью формулы n-ого члена последовательности (аналитический способ). Формула общего члена позволяет вычислить член последовательности с любым заданным номером. Например, если хn=3n+2, то х5=3. 5+2=17; х45=3. 45+2=137. Рекуррентный способ Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro– возвращаться). Например, последовательность, заданную правилом а1=1; аn+1= аn +3 можно записать с многоточием: 1; 4; 7; 10; 13; …

- Перечислите, какими свойствами обладают числовые последовательности?
Учащиеся перечисляют свойства числовых последовательностей, а учитель, по мере вспоминания, вывешивает на доске таблички с названиями.

Определите вид последовательности

1) 1, 2, 3, 4, 5, : - последовательность натуральных чисел;

 2) 2, 4, 6, 8, 10, :- последовательность четных чисел;

 3) 1, 4, 9, 16, 25, : - последовательность квадратов натуральных чисел;

4) 2, 3, 5, 7, 11, : - последовательность простых чисел;

5) 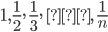         - последовательность чисел, обратных натуральным.

6) 1,2,3,4,6,8,12,24 – последовательность чисел, являющихся делителями числа 24

Задания №1:
Проверьте на монотонность числовые последовательности, заданные формулой - го члена. Ответ обоснуйте с места.

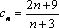
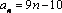
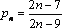
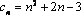
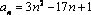
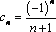
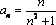
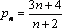
Задания №2:
Является ли ограниченной последовательность, заданная формулой - го члена. Ответ обоснуйте.

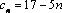
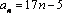
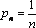
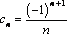
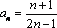
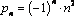
Задание № 3:Продолжите числовой ряд и задать последовательность следующими способами:

– Формулой n-го члена;
– Таблицей;
– Графиком;
– Словесным описанием.

Ответ обоснуйте у доски
группа «α»                                                    ответ
1. 18, 20, 24, 32,?,…;                                        48
2.  6, 8, 10, 11, 14, 14,?,…;                               18
3.  7, 13, 24, 45,?,…;                                         86
4.  4, 5, 7, 11, 19,?,….                                       35 

группа «β»
1.  6, 7, 9, 13, 21,?,…;                                        37
2.  64, 48, 40, 36, 34,?,…;                                  33
3.  15, 13, 12, 11, 9, 9,?,…;                                6
4.  7, 14, 10, 12, 14, 9,?,….                                19

группа «γ»
1.  172, 84, 40, 18,?,…;                                       7
2.  1, 5, 13, 29,?,…;                                             61
3.   0, 3, 8, 15,?,…;                                              24
4.  4, 7, 9, 11, 14, 15, 19,?,….                             19

1. Физминутка

1. Работа по теме урока

Вопрос: Какая последовательность называется возрастающей?

Опр.1 Последовательность (у_n) называют возрастающей, если каждый её член (кроме первого) больше предыдущего: y_{1 2 3 n n+1} 

Пример 1 (на доске) Доказать, что последовательность является возрастающей y_n = 2ⁿ

Ответ: 2, 4, 8, 16, 32, …

Н-р:    1, 1 , 1 , 1 , … , 1 , …  последовательность убывающая

               2   3   4          n

Опр.2 Последовательность (у_n) называют убывающей, если каждый её член (кроме первого) меньше предыдущего: y₁  y₂  y₃  . . . y_n  y_n+1  . . .

Пример 2 (на доске)Доказать, что последовательность является убывающей

 y_n=  1   ⁿ

      3

Ответ: 1,  1 ,   1 ,   1 ,    1 , …  

                        3     9     27   81

Н-р:    1, _  1 ,  1 ,  _  1 , … , (- 1)^n-1 1 , …  немонотонная последовательность

                        2    3        4                      n

Вывод: (обобщим примеры 1 и 2и сделаем вывод)

1. Если n 1, то последовательность    y_n = aⁿ возрастает

2. Если 0_n = aⁿ убывает.

6. Закрепление изученного

Задача: №224

1) а_n = 2n + 3; 3) а_n = 100 – 10n²;

а₁ = 2  1 + 3 = 5; а₁ = 100 – 10  1² = 90;

а₂ = 2  2 + 3 = 7; а₂ = 100 – 10  2² = 60;

а₃ = 2  + 3 = 9. а₃ = 100 – 10  3² = 10.

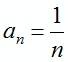  ; а₁ = 1; а₂ =  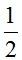; а₃ =  .

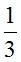Задача 

Найдите несколько начальных членов возрастающей последовательности всех натуральных чисел, кратных семи. Укажите её восьмой, десятый, тридцать седьмой, n-ый члены.  

Ответ: х = 7n

х₁ = 7*1 = 7                                                 х₈ = 7*8 = 56

х₂ = 7*2 = 14                                               х₁₀ = 7*10 = 70

х₃ = 7*3 = 21                                               х₃₇ = 7*37 = 256

             х₄ = 7*4 = 28

Тестовая проверочная работа

1. По заданной формуле n-го члена последовательности вычислите первые 3 члена последовательности              y_n = n² – 4

О  (-3, 0, 5)               Н  (-2, 0, 2)                    Д  (3, 0, 5)

2. Найти третий член последовательности

              y_n = n + 1

                      n² – 8

Н  (4)                         О  (-2)                  К   1

                                                                     4

3. Найти четвёртый член последовательности    у_n  = 2ⁿ

О  (8)                А  (16)                С  (20)

 Задание 3    Подобрать формулу n-го члена последовательности  2, 3, 4, 5, …

Ответ: y_n = n  + 1

y₁ = 1 + 1 = 2

y₂ = 2 + 1 = 3

            y₃ = 3 + 1 = 4

            y₄ = 3 + 1 = 5

4. Подберите формулу n-го члена последовательности  3, 6, 9, 12, 15, …

Ч  (3n)               В  (n + 3)             Т  (2n + 1)

7.Подведение итогов. 

Итак, мы познакомились с  понятием числовая последовательность и рассмотрели способы её задания.

Ответьте на вопросы:

Что такое последовательность?

Какие виды последовательностей вы узнали?

Какие способы задания вы узнали?

О каких ученых и их трудах вы узнали?

8. Домашнее задание:

        №  224(чет), №226

Урок по теме «Числовая последовательность» является первым уроком темы «Арифметическая прогрессия».

Цель урока: познакомить с понятием последовательности, способами задания последовательности; выработать умения использовать индексные обозначения и находить n-й член последовательности по заданной формуле.

Задачи урока:

Образовательные: формирование представления о последовательности, знаний о способах задания числовых последовательностей, умений находить члены последовательности по предложенной формуле, а также умений находить саму формулу, задающую последовательность.

Развивающие: развитие умений сравнивать и анализировать, обобщать информацию, делать выводы.

Воспитательные: воспитание навыков самоконтроля, культуры общения, воспитание таких качества характера, как настойчивость в достижении цели, умение не растеряться в проблемной ситуации.

Деятельность учащегося была направлена на решение поставленных задач и развитие самого себя.

Урок был построен таким образом, что учащийся самостоятельно делал все выводы. Данный урок явился не только вводным, но и уроком подготовки к ГИА. Все задачи, решаемые в ходе него, были взяты из сборника «Подготовка к ГИА». Это послужило мотивацией для ученика, так как он заинтересован в успешной сдачи экзамена. Задачи были подобраны с учетом уровневой дифференциации при подготовки к ГИА, а так же с учетом индивидуальных особенностей ученика.

Использованная технология урока характерна для данного типа и вида урока и рациональна для достижения поставленных целей. В связи с тем, что учащийся по своей подготовленности сможет принять активное участие в учебной деятельности, было выбрано сочетание следующих средств и методов работы: наглядно-словесные, практические, создание ситуации успеха. Процесс обучения строился на постепенном усложнении содержания. Главный акцент на уроке делался на закрепление навыков учащегося при выполнении упражнений, а также на развитие воображения, творческой активности учащихся, а также памяти, внимания, логического мышления.

Контроль усвоений знаний, умений и навыков был предусмотрен в виде работы по учебнику.

На уроке целесообразно использовались возможности компьютера, и сделанной презентации для быстрой проверки домашнего задания, показа презентаций.

Этап рефлексии. На данном этапе происходило осмысление данных знаний, соотнесение их к применению на практике, обсуждение, выработка собственных позиций, обмен мнениями, побуждение к дальнейшему расширению поля информации.

При подведении итога урока учащийся имел возможность высказать свою точку зрения об уроке, внести предложения, пожелания. Домашнее задание было оптимальным и задано с учетом уровневой дифференциации – это задачи из «банка открытых заданий ГИА», а так же были предложены задачи практического содержания.

Вывод:

План урока был выполнен, цель урока достигнута. Деятельность учащегося оцениваем следующим образом: на уроке чётко проявился интерес к предмету, эмоциональное состояние учащегося было приподнятым в начале и к концу урока. На уроке присутствовали самоконтроль и самокоррекция со стороны обучающегося. Была высока степень самостоятельности в учебной деятельности.

На уроке созданы атмосферы взаимной заинтересованности в работе учащихся и учителя:

•оценка деятельности ученика не только по конечному результату (правильнонеправильно), но и по процессу его достижения;

•поощрение стремления ученика находить свой способ решения задачи, анализировать способы других учеников в ходе урока, выбирать и осваивать наиболее рациональные; •создание педагогических ситуаций, позволяющих каждому ученику проявлять инициативу, самостоятельность, избирательность в способах работы;

•создание ситуации выбора и успеха;

•создание условий для актуализации и обогащения субъектного опыта учащихся; •создание обстановки для естественного самовыражения ученика. Учебная деятельность на уроке спланирована, с учётом здоровье - сберегающей технологии обучения, способствует сохранению здоровья детей, а именно:

• своевременная подготовка к уроку и его мобилизующее начало;

• доброжелательная атмосфера, способствующая положительному эмоциональному настрою;

• чёткая организация учебного труда;

• антистрессовые моменты, выраженные в стимулировании учащихся;

• смена видов деятельности учащихся;

• динамическая пауза. Организация учебной деятельности с учётом ИКТ позволяет учащимся с использованием презентации проверить групповую, парную работу. С другой стороны, надпредметным компонентом результата деятельности учащихся на уроке является приобщение их к процессу творчества, открытия для себя нового, осознание чувства сопричастности к общему успеху.

Родители 9б класса