Конспект. Паралельні та перпендикулярні прямі. Ознаки паралельності прямих
Прямі, що перетинаються
Означення прямих, що перетинаються.
| Дві прямі називаються такими, що перетинаються в даній точці, якщо ця точка належить кожній із цих прямих.
Прямі а і b перетинаються в точці О. | 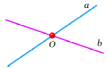
a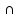 b = О b = О |
Означення кута між двома прями
| Кутом між двома прями, що перетинаються вважають менший із кутів. | 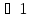 або або 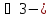 кут між прямими кут між прямими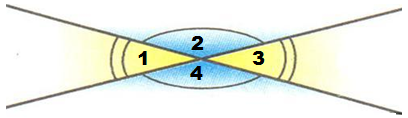
|
Перпендикулярні прямі
Означення перпендикулярних прямих
| Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. Пишуть: a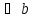 | 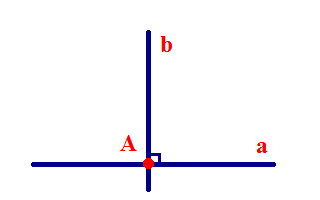
|
Означення перпендикулярних відрізків або променів
| Відрізки або промені називаються перпендикулярними, якщо вони лежать на перпендикулярних прямих. | 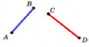
|
Теорема (властивість перпендикулярних прямих)
| Через кожну точку прямої можна провести перпендикулярну їй пряму, і тільки одну. | 
|
Теорема(властивість перпендикулярних прямих)
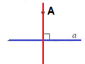
| Через точку, що не лежить на прямій, можна провести пряму перпендикулярну даній, і тільки одну.
| 
|
.Означення перпендикуляра до даної прямої
| Перпендикуляром до прямої називається відрізок, опущений з даної точки до прямої під прямим кутом. Кінець відрізка, який лежить на прямій, називається основою перпендикуляра. Точка В – основа перпендикуляра АВ. | 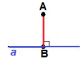
АВ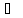 а а |
Означення відстані від точки до прямої.
| Відстанню від точки до прямої називається довжина перпендикуляра, опущеного з точки на пряму. | 
АВ – відстань від точки А до прямої а. |
Паралельні прямі
Означення паралельних прямих.
| Дві прямі на площині називаються паралельними, якщо вони не перетинаються. Пишуть: a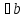 . . | 
|
Аксіома паралельних прямих
| Через точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній прямій. | 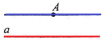
|
Означення відстані між паралельними прямими
| Відстанню між паралельними прямими називається відстань від будь-якої точки однієї прямої до другої прямої.
Довжина відрізка АВ – відстань між паралельними прямими a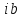 . . | 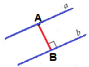
|
Означення
| Два відрізки або промені називаються паралельними, якщо вони лежать на паралельних прямих. | 
АВ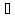 СD, BC СD, BC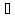 AD AD |
Кути, утворені при перетині двох прямих третьої прямою (січною)
Означення січної
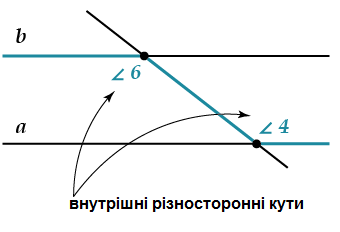
| Пряму с називають січною відносно прямих а і b, якщо вона перетинає їх у двох точках. |
При перетині двох прямих січною утворюється вісім нерозгорнутих кутів, які мають спеціальні назви.
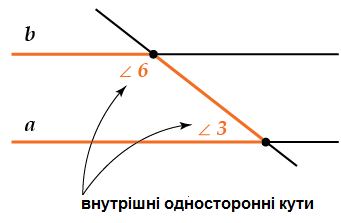
| Внутрішні різносторонні кути: 3 і 5; 4 і 6. Внутрішні односторонні кути: 4 і 5; 3 і 6. Відповідні кути: 1 і 5; 3 і 7; 2 і 6; 4 і 8. Зовнішні різносторонні кути: 1 і 7; 2 і 8. Зовнішні односторонні кути: 1 і 8; 2 і 7. | 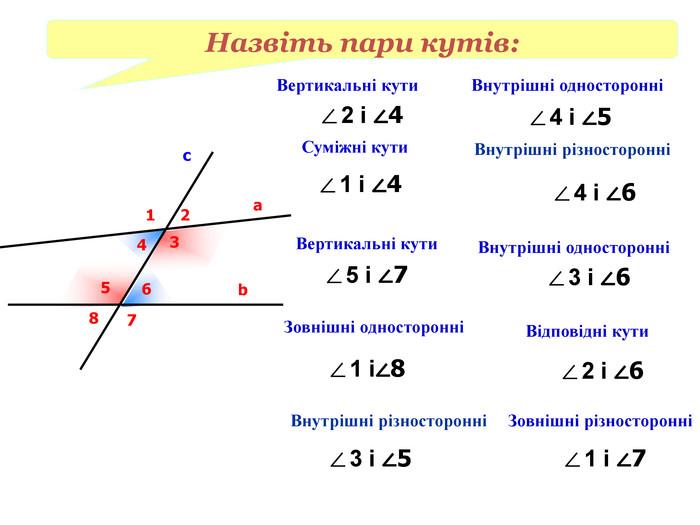
|
Ознаками називають найважливіші теореми, у яких зазначається, за яких умов правильні ті чи інші твердження.
Види кутів при паралельних прямих а і b та січній с
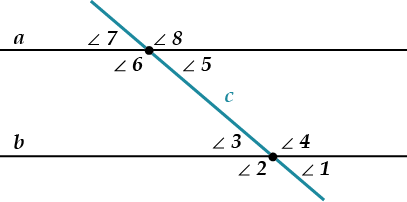
Ознаки паралельності прямих.
Теореми
| 1.Дві прямі паралельні, якщо при перетині із січною вони утворюють рівні внутрішні різносторонні кути. Якщо  то то  . . | |
| 2.Дві прямі паралельні, якщо при перетині їз січною вони утворюють внутрішні односторонні кути, сума яких дорівнює 1800. або  то то  . . |
| 3. Дві прямі паралельні, якщо при перетині із січною вони утворюють рівні відповідні кути. ; або  , то , то 
|
| 4. Дві прямі, перпендикулярні до третьої, паралельні між собою.
Якщо  с і с і  с, то с, то  | 
|
| 5. Дві прямі паралельні до третій, паралельні одна одній. Якщо  i i  , то , то  | 
|








 b = О
b = О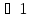 або
або 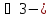 кут між прямими
кут між прямими
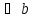




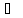 а
а
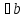 .
.

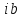 .
.

 СD, BC
СD, BC