Конспект-план интерактивного рабочего листа по теме «ЕГЭ по информатике решение №4»

М.Ю. Куликовский

Конспект-план интерактивного рабочего листа по теме «ЕГЭ по информатике решение №4»

Ссылка для учителей: https://coreapp.ai/app/preview/lesson/635e69da5de97c3cbb08f652

Ссылка для учеников:

https://coreapp.ai/app/player/lesson/635e5b8a3befe970181d41c5

Цель: Ученик должен иметь представление о кодировании и декодировании информации, а также научиться применять эти знания и самостоятельно решать задания.

1. Вводная часть

1. Типичные ошибки и рекомендации по их предотвращению

1. Теоретическая часть

• Рассмотрен термин «кодирование» и приведен пример

• Рассмотрены термины: декодирование, префиксный код, постфиксный код

• Объяснено: условие Фано, обратное условие Фано

• Приведен пример декодирования

1. Разбор двух заданий

• Первое задание:

Задание:

Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).

Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.

Решение:

• Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:

О - 0 - 00

В - 1 - 01

Д - 2 - 10

П - 3 - 11

А - 4 - 100

• Теперь закодируем последовательность букв из слова ВОДОПАД:

010010001110010

• Разобьем результат на группы из трех символов справа налево, чтобы перевести их в восьмеричную систему счисления:

010 010 001 110 010

 ↓    ↓   ↓   ↓   ↓

 2    2   1   6   2

Результат: 22162

Теоретическое решение ЕГЭ данного задания по информатике, видео: https://www.youtube.com/watch?v=WcTx2qzkw_o

• Второе задание:

Задание:

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

Какой набор букв закодирован двоичной строкой 1100000100110?

Решение:

• Сделаем дерево, согласно кодам в таблице:

• Сопоставим закодированное сообщение с кодами в дереве:

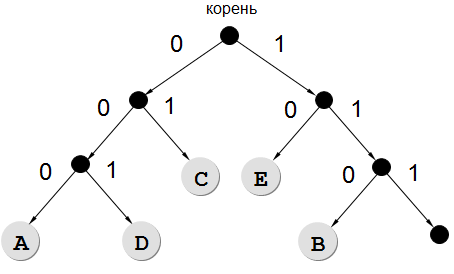
110 000 01 001 10

Результат: b a c d e.

Теоретическое решение ЕГЭ данного задания по информатике, видео: https://www.youtube.com/watch?v=w6B1yWXb3xo

1. Самостоятельное решение учениками пяти заданий

• Первое задание

Решение:

• Рассмотрим пример из условия задачи:

Было 23₁₀

Стало 0010100110₂

• Где сами цифры исходного числа (выделим их красным цветом):

0010100110 (0010 - 2, 0011 - 3)

• Первая добавленная цифра 1 после двоичной двойки — это проверка четности (1 единица в 0010 — значит нечетное), 0 после двоичной тройки — это также проверка нечетности (2 единицы в 0011, значит — четное).

• Исходя из разбора примера решаем нашу задачу так: поскольку «нужные» нам цифры образуются из групп по 4 числа в каждой плюс одно число на проверку четности, то разобьем закодированное сообщение на группы по 5, и отбросим из каждой группы последний символ:

• разбиваем по 5:

01100 01010 01001 00110

• отбрасываем из каждой группы последний символ:

0110 0101 0100 0011

• Результат переводим в десятичную систему:

0110 0101 0100 0011

↓ ↓ ↓ ↓

6 5 4 3

Ответ: 6 5 4 3

• Второе задание

Решение:

 1 вариант решения основан на логических умозаключениях:

• Найдём самые короткие возможные кодовые слова для всех букв.

• Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).

• Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).

• Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.

• Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

 2 вариант решения:

• Будем использовать дерево. Влево откладываем 0, вправо — 1:

• Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:

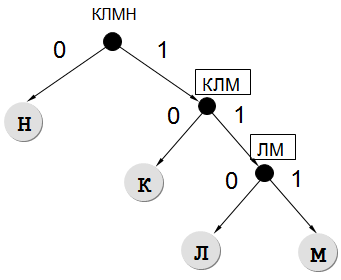
(Н) - 0 - 1 символ

(К) - 10 - 2 символа

(Л) - 110 - 3 символа

(М) - 111 - 3 символа

• Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

Ответ: 9

• Третье задание

Решение:

• Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).

• Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.

Результат: 00

• Четвертое задание

Решение:

• Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:

• Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:

• Перепишем сверху вниз получившееся кодовое слово для Д: 101

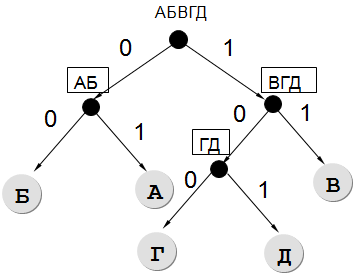
Результат: 101

• Демоверсия ЕГЭ 2018 информатика (ФИПИ)

Решение:

• Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.

• При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100

1. Заключение