11 класс
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Урок №25
Тема: Тригонометрические функции, их свойства и графики. Область определения и множество значений тригонометрических функций.
Тип: урок изучения нового материала.
Цель: познакомить учащихся с понятием области определения и множества значений тригонометрических функций, а также развить навыки работы с графиками этих функций и применение полученных знаний в решении задач.
Автор разработки: учитель математики и информатики, Попов Дмитрий Сергеевич.
ХОД УРОКА
I. Организационный момент
- Здравствуйте, ребята! Проверьте готовность к уроку: у вас на парте должны лежать учебники, тетради, ручка, карандаш и линейка.
Учитель спрашивает дежурного по классу об отсутствующих на уроке.
II. Проверка домашнего задания
- Ребята, что вам было задано для выполнения дома?
- Скажите, какие задания вам было трудно выполнить и/или вы не выполнили?
III. Постановка темы и целей урока
- В том году мы начали изучать раздел математики под названием «Тригонометрия». Кто может ответить на вопрос: «Что изучает тригонометрия?»
Учитель выслушивает ответы учащихся
- Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение. Ребята, а назовите те тригонометрические функции, которые вы изучили?
- Да, начиная с 8 класса, вы уже знакомились с синусом, косинусом, тангенсом и котангенсом. Начиная с сегодняшнего занятия, мы будем более подробно рассматривать тригонометрические функции, их свойства и графики. На этом уроке мы будем рассматривать такую тему «Область определения и множество значений тригонометрических функций».
- Откройте тетради, запишите дату и тему урока.
- Ребята, какие цели мы можем поставить перед собой на сегодняшнем уроке?
IV. Изучение нового материала
- Начнём с рассмотрения функции у=sin(x). Значения х, при которых определена функция у = sin(х) – это любые действительные числа. То есть, какие бы вы числа не брали, вы все равно сможете «вытащить» и вычислить свой синус. С множеством значений, т.е. именно со значением самой функции (с у), нужно быть внимательнее, так как множество значений, которые принимает сама функция у = sin(х) – это интервал от минус единицы до единицы включительно. Исходя из вышесказанного, можно сделать вывод, что 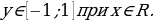
Учитель на доске делает запись: 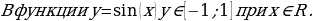
- Теперь встаёт вопрос: как это можно увидеть на графике?
У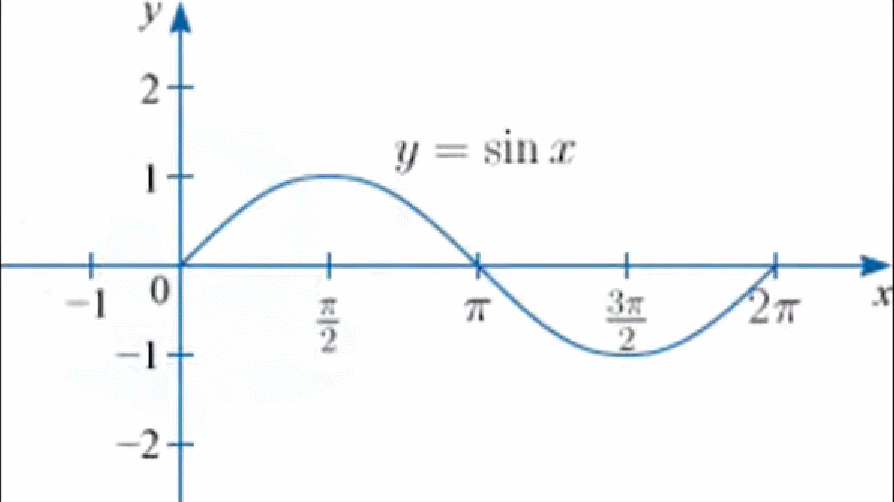 читель строит график функции
читель строит график функции 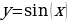 , комментируя:
, комментируя:
Хоть здесь график идёт только в правую сторону, он точно также продолжается в реальности и в левую сторону, т.е. в реальности мы с вами можем идти от -∞, включая ноль, и до +∞ (это по оси х). А вот у у нас «застрял». Как мы видим, максимальное значение по оси у равно 1, а минимальное -
-1.
Получается, что весь график у нас, как бы он «волнами» не шёл, эти «волны» всегда будут лежать от -1 до 1.
- Теперь рассмотрим функцию 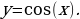 Значения х, при которых определена функция у = соs(х) – это любые действительные числа. Заметим, что у косинуса такая же область определения, то есть все х, которые являются действительными числами. Множество значений, которые принимает сама функция у = cos(х) – это интервал от минус единицы до единицы включительно. Обратите внимание: то же самое, что и у синусов. У cos(x) точно такие же область определения и множество значений, что и у sin(x).
Значения х, при которых определена функция у = соs(х) – это любые действительные числа. Заметим, что у косинуса такая же область определения, то есть все х, которые являются действительными числами. Множество значений, которые принимает сама функция у = cos(х) – это интервал от минус единицы до единицы включительно. Обратите внимание: то же самое, что и у синусов. У cos(x) точно такие же область определения и множество значений, что и у sin(x).
Учитель на доске делает запись: 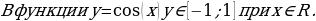
Т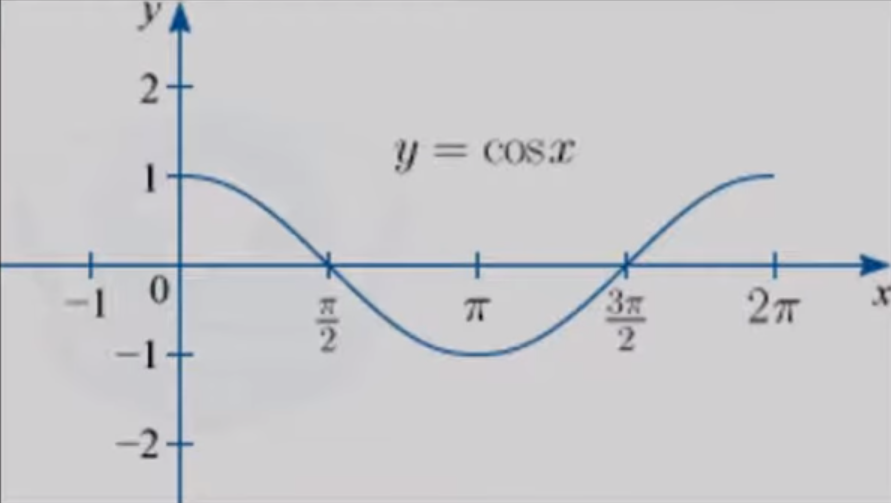 еперь вам может быть непонятно: если область определения и множество значений функций одинаковые, то почему они называются по-разному и в чём заключается разница, откуда она взялась? Давайте разберёмся!
еперь вам может быть непонятно: если область определения и множество значений функций одинаковые, то почему они называются по-разному и в чём заключается разница, откуда она взялась? Давайте разберёмся!
Учитель строит график функции 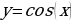 .
.
- Если вы внимательно посмотрите на графике, то сможете заметить, что у синуса мы шли от нуля, но у косинуса мы идём от 1. Здесь оба графика взяты на некоторую часть, но мы помним, что график бесконечен в одну сторону и бесконечен в другую.
- Теперь переходим к более сложной функции 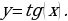 Значения х, при которых определена функция у = tg(х) – это все числа, исключая
Значения х, при которых определена функция у = tg(х) – это все числа, исключая 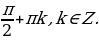 Как вы увидели, у тангенса всё сложнее. Дело в том, что, если вы вспомните ещё геометрическое определение тангенса, то tgx =
Как вы увидели, у тангенса всё сложнее. Дело в том, что, если вы вспомните ещё геометрическое определение тангенса, то tgx = 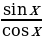 , то есть у нас появляется дробь. А если дробь, то сразу вспоминаем некие ограничения (мы не можем делить на ноль), то есть те точки, в которых мы будем нулём, нужно «выколоть», их нельзя брать, мы их запретим.
, то есть у нас появляется дробь. А если дробь, то сразу вспоминаем некие ограничения (мы не можем делить на ноль), то есть те точки, в которых мы будем нулём, нужно «выколоть», их нельзя брать, мы их запретим.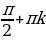 – что это за числа? Это 90˚ и 270˚, то есть те точки, которые у нас находятся на вертикальной оси, те точки в которых у нас косинус будет равен нулю. То есть, чтобы на 0 не делить, мы эти точки будем исключать. В области определения у нас уже есть исключения.
– что это за числа? Это 90˚ и 270˚, то есть те точки, которые у нас находятся на вертикальной оси, те точки в которых у нас косинус будет равен нулю. То есть, чтобы на 0 не делить, мы эти точки будем исключать. В области определения у нас уже есть исключения.
С множеством значений всё наоборот. Раньше мы там ограничивали наш у (у синусов и косинусов), а тангенса всё просто: «где у хочет гулять, там он и гуляет». Множество значений, которые принимает сама функция у = tg(х) – это любые действительные числа.
Учитель на доске делает запись: 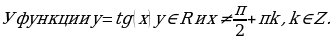
- Как это можно увидеть на графике?
Учитель строит график функции 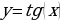 , комментируя:
, комментируя:
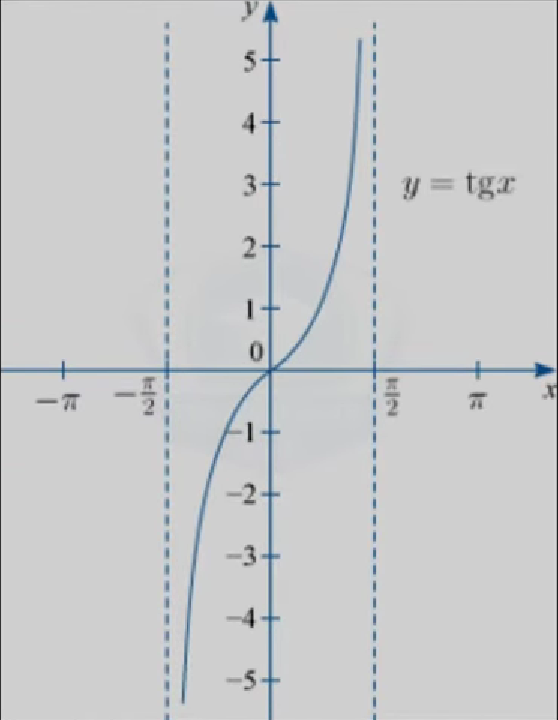
Все точки, которые выделены пунктиром, мы должны с вами «выкалывать», мы не должны их видеть. График тангенса уходит до бесконечности вверх и до бесконечности вниз. Более того, график повторится после пунктирной линии, как в одну сторону, так и во вторую.
- A теперь переходим к последней на сегодняшней день функции – у = ctg(x). Данная функция, к сожалению, редко встречается в задачах, но мы её тоже должны разобрать.
Значения х, при которых определена функция у = сtg(х) – это все числа, исключая 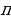 k, k ∈ Z. Множество значений, которые принимает сама функция у = ctg(х) – это любые действительные числа.
k, k ∈ Z. Множество значений, которые принимает сама функция у = ctg(х) – это любые действительные числа.
Н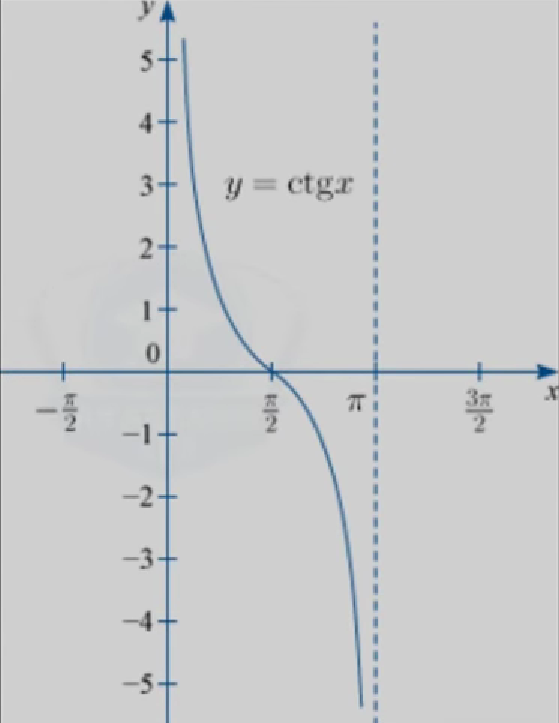 а графике это выглядит следующим образом:
а графике это выглядит следующим образом:
Учитель рисует график:
От тангенса отличается тем, что дуга уже идёт в другую сторону, более того график смещён.
V. Решение заданий
Учитель проводит фронтальный опрос по №№691, 692.
Далее учитель вызывает к доске учащихся к доске для решения №№693, 694 (1,2,3), 695 (2), 696 (2,3) (количество заданий определяет учитель в зависимости от оставшегося времени).
VI. Домашнее задание
Изучить §38.
Выучить область определения и множество значений основных тригонометрических функций.
Выполнить задания на карточках (приложение 1).
VII. Рефлексия
- Ребята, что нового вы узнали на уроке?
- Что было интересным?
- Что вызвало трудности?
VIII. Подведение итогов урока. Оценивание учебной деятельности учащихся
Учитель выставляет оценки за урок.







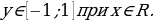
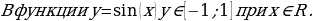
 читель строит график функции
читель строит график функции 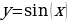 , комментируя:
, комментируя: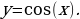 Значения х, при которых определена функция у = соs(х) – это любые действительные числа. Заметим, что у косинуса такая же область определения, то есть все х, которые являются действительными числами. Множество значений, которые принимает сама функция у = cos(х) – это интервал от минус единицы до единицы включительно. Обратите внимание: то же самое, что и у синусов. У cos(x) точно такие же область определения и множество значений, что и у sin(x).
Значения х, при которых определена функция у = соs(х) – это любые действительные числа. Заметим, что у косинуса такая же область определения, то есть все х, которые являются действительными числами. Множество значений, которые принимает сама функция у = cos(х) – это интервал от минус единицы до единицы включительно. Обратите внимание: то же самое, что и у синусов. У cos(x) точно такие же область определения и множество значений, что и у sin(x).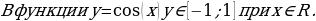
 еперь вам может быть непонятно: если область определения и множество значений функций одинаковые, то почему они называются по-разному и в чём заключается разница, откуда она взялась? Давайте разберёмся!
еперь вам может быть непонятно: если область определения и множество значений функций одинаковые, то почему они называются по-разному и в чём заключается разница, откуда она взялась? Давайте разберёмся!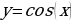 .
. 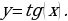 Значения х, при которых определена функция у = tg(х) – это все числа, исключая
Значения х, при которых определена функция у = tg(х) – это все числа, исключая 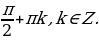 Как вы увидели, у тангенса всё сложнее. Дело в том, что, если вы вспомните ещё геометрическое определение тангенса, то tgx =
Как вы увидели, у тангенса всё сложнее. Дело в том, что, если вы вспомните ещё геометрическое определение тангенса, то tgx = 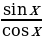 , то есть у нас появляется дробь. А если дробь, то сразу вспоминаем некие ограничения (мы не можем делить на ноль), то есть те точки, в которых мы будем нулём, нужно «выколоть», их нельзя брать, мы их запретим.
, то есть у нас появляется дробь. А если дробь, то сразу вспоминаем некие ограничения (мы не можем делить на ноль), то есть те точки, в которых мы будем нулём, нужно «выколоть», их нельзя брать, мы их запретим.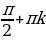 – что это за числа? Это 90˚ и 270˚, то есть те точки, которые у нас находятся на вертикальной оси, те точки в которых у нас косинус будет равен нулю. То есть, чтобы на 0 не делить, мы эти точки будем исключать. В области определения у нас уже есть исключения.
– что это за числа? Это 90˚ и 270˚, то есть те точки, которые у нас находятся на вертикальной оси, те точки в которых у нас косинус будет равен нулю. То есть, чтобы на 0 не делить, мы эти точки будем исключать. В области определения у нас уже есть исключения.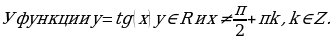
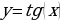 , комментируя:
, комментируя:
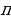 k, k ∈ Z. Множество значений, которые принимает сама функция у = ctg(х) – это любые действительные числа.
k, k ∈ Z. Множество значений, которые принимает сама функция у = ctg(х) – это любые действительные числа. а графике это выглядит следующим образом:
а графике это выглядит следующим образом: 









