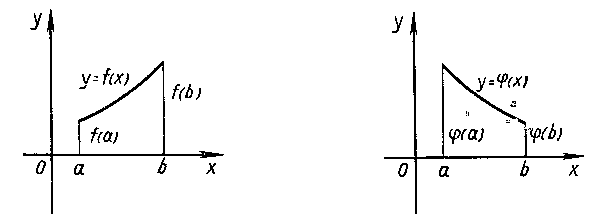8
Тема урока. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке.
Цели: создание условий для получения алгоритма и использования его для нахождения наибольшего и наименьшего значений функций на промежутке.
Задачи:
Предметные:
Повторить основные понятия по теме «Применение производной для исследования функций»: определение стационарных и критических точек, нахождение монотонности и точек экстремума функции по графику и с помощью производной.
Сформулировать основные теоретические положения, рассмотреть алгоритм решения задач, отработать шаги алгоритма, рассмотреть частные случаи научить находить наибольшее и наименьшее значения непрерывной функции на промежутке;
Метапредметные:
Развивать речь, внимание.
Развивать умение работать в паре, умение читать график функции, анализировать, сравнивать, обобщать и делать выводы, развивать исследовательские умения.
Развивать умение выделять главное при работе с текстом учебника.
Развивать умение ставить новые задачи в учебной и познавательной деятельности
Личностные:
Воспитывать умение самостоятельно работать, умение общаться.
Воспитывать навыки взаимоконтроля и самоконтроля.
Воспитывать интерес к истории математики как науки.
Ход урока
1.Оргмомент. Здравствуйте ребята. Садитесь. Начнем наш урок.
Изучением какой темы мы занимаемся вот уже несколько уроков?(Производная функции). Чему вы научились, изучая данный материал?(находить производные функций, исследовать их на монотонность и экстремумы, строить график). Какую не менее важную характеристику функции мы ещё не находили? (наим. и наиб. значения функции).
Поэтому тема нашего урока “Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. Что вы должны узнать и чему научиться на этом уроке?
Сегодня мы вместе с вами научимся с помощью производной находить наибольшее и наименьшее значения непрерывной функции на отрезке.
Эпиграфом к уроку возьмем слова русского математика 19 века Пафнутия Львовича Чебышева. Он говорил, что “особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды”. (Слайд 1)
2. Актуализация знаний и умений.
1) Вы уже накопили некоторый опыт нахождения производной и исследования функции. Ответьте на вопросы:
Что значит исследовать функцию на монотонность?
Сформулируйте теоремы о монотонности функции.
Какие точки называют точками экстремума?
Сформулируйте теорему об экстремумах.
Каков алгоритм исследования функции на монотонность и экстремумы.
2) Назовите стационарные и критические точки, промежутки возрастания и убывания по графику функции (Слайд 2)
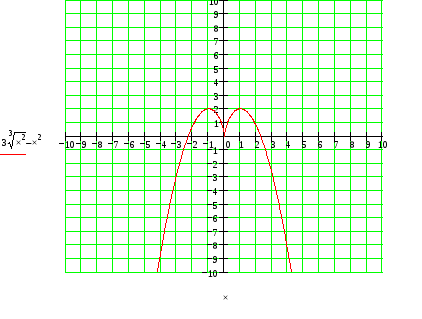
3)Назовите по данным таблицы промежутки возрастания и убывания функции, а также точки максимума и точки минимума. (Слайд 3)
| x | (-∞; -1) | -1 | (-1; 0) | 0 | (0; 2) | 2 | (2; +∞) |
| 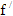 (x) (x)
| - | 0 | + | 0 | - | 0 | + |
| f(x) | 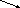
| -1 min | 
| 0 max | 
| -3 min | 
|
4) Используя график функции, укажите наибольшее и наименьшее значения функции. (Слайд 4)
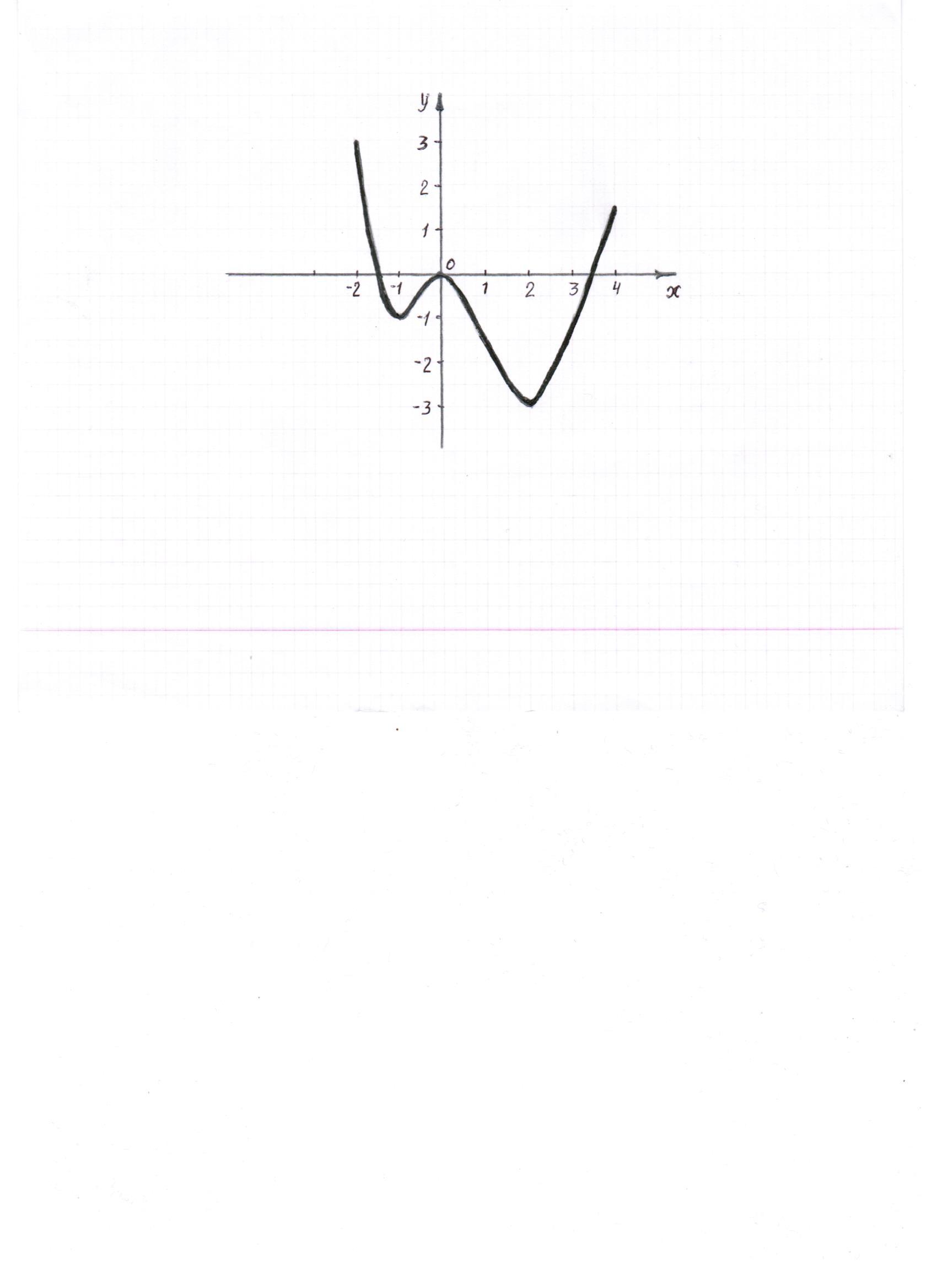
Обобщение.
3.Мотив изучения новой темы.
Скажите пожалуйста, с помощью чего мы можем найти наибольшее и наименьшее значения функции?
( с помощью графика функции). А всегда ли это можно делать?..
Сегодня мы будем искать более простые пути решения данной задачи.
Итак. Тема урока «Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке».
Большую часть своих усилий человек тратит на поиск наилучшего, или как часто говорят, оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества. Не все такие задачи поддаются математическому описанию, не для всех из них найдены короткие пути решения. Однако часть таких задач – задач на оптимизацию, поддается исследованию с помощью методов математического анализа – это задачи, которые можно свести к нахождению наибольшего и наименьшего значения функции. И исходя из большой практической значимости, задание на нахождение наибольшего и наименьшего значений функции на отрезке включены в ЕГЭ по математике.
Наиболее важной ситуацией является следующая: функция y=f(x) задана на [a;b] и имеет производную во всех точках этого отрезка. Необходимо найти её наибольшее и наименьшее значение на [a;b].
4.Организация (исследовательской) работы в парах
Сегодня я предлагаю вам выступить в роли исследователей. Работая в парах, каждый получает задание, выполнение которого должно привести вас к важным теоретическим выводам и алгоритму решения таких задач – задач на нахождение наибольшего и наименьшего значений функции на отрезке. На выполнение работы – 10 минут
1.Анализ результатов работы групп.
Подведём итоги. Каковы результаты работы?
Выводы обсуждают с помощью мозгового штурма. Обобщают, уточняют и озвучивают.
Итак, в ходе работы вы получили несколько важных выводов. Послушаем их.
Должны быть сделаны следующие выводы: (Слайд 5)
Если функция непрерывна на отрезке [a;b], то она достигает на нем своего наибольшего и своего наименьшего значения.
Наименьшего и наибольшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Если наибольшее ( или наименьшее) значения функции достигается внутри отрезка, то либо в критических точках, либо в стационарных точках.
Если функция y=f(x) не имеет на отрезке[a;b] критических и стационарных точек, тогда
а) если f´(x)0 на (а; b)f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( в левом конце промежутка).
б) если f´(x) b) f(x) – убывает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке а (в левом конце промежутка), а наименьшее в точке b ( в правом конце промежутка).
На основании выше сказанного вы сформировали алгоритмы. Давайте их проверим с помощью учебника (стр.217). Соответствуют ли ваши алгоритмы данному алгоритму?
2.Усвоение алгоритма
Для чего нам в математике нужны алгоритмы? (Чтобы научиться решать задачи.)
Известный венгерский, швейцарский и американский математик Дьёрдь По́йа говорил:
Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах, или игре на фортепьяно: научиться этому можно, лишь подражая избранным образцам и постоянно тренируясь…
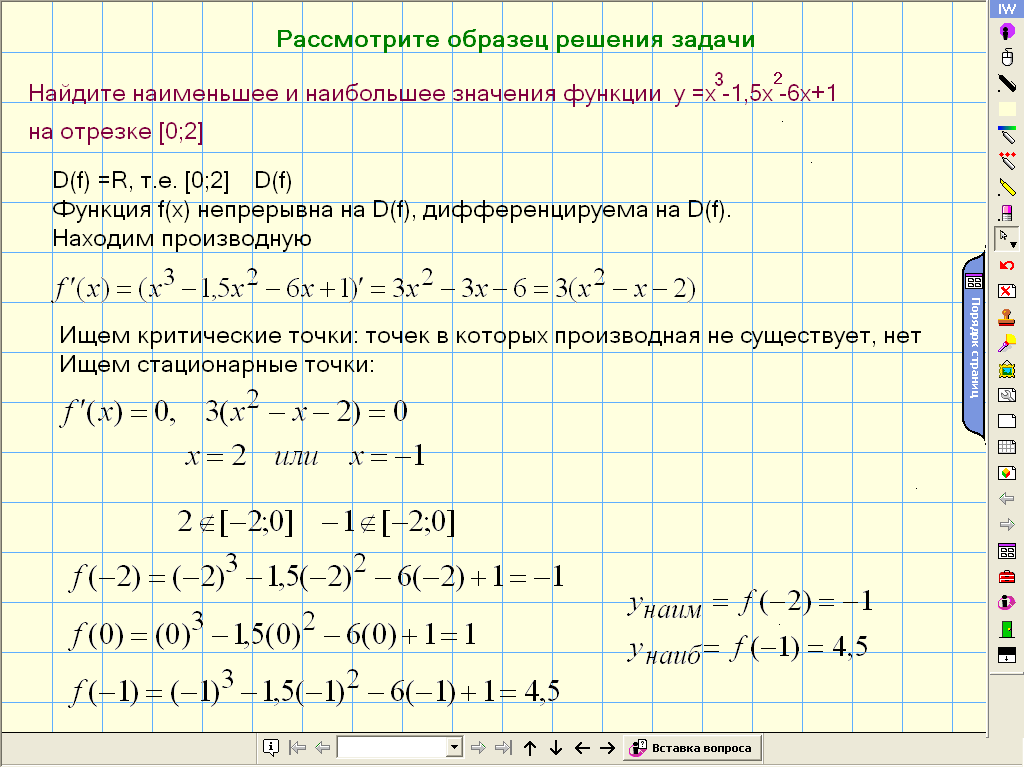
Поэтому, я предлагаю вам рассмотреть образец решения задачи (на интерактивной доске) Выделите шаги алгоритма в её решении.
Есть ли шаги, которые приведены в решении, но не прописаны в нашем алгоритме?
Как дополнить наш алгоритм
Какие шаги алгоритма мы умеем выполнять?
Какие шаги новые для нас?
Алгоритм
Найти D(f), содержится ли [a;b] в D(f)
Определить непрерывность и дифференцируемость функции на D(f)
Найти производную f´(x)
Найти стационарные и критические точки функции.
Выбрать те , которые лежат внутри отрезка [a;b]
Вычислить значения функции y=f(x), в отобранных на пятом шаге и на концах отрезка
Выбрать среди этих значений наименьшее ( это будет унаим) и наибольшее ( это унаиб)
Все ли понятно? Решим такой пример у доски.
2. Найдите наибольшее и наименьшее значения функции
f(x) =x4-2x2-3 на отрезке [0;2] ( 1 ученик у доски, остальные на месте, само и взаимопроверка)
3. Рассмотрите следующее задание. Решите его самостоятельно. (1 ученик у доски, остальные на месте, само и взаимопроверка)
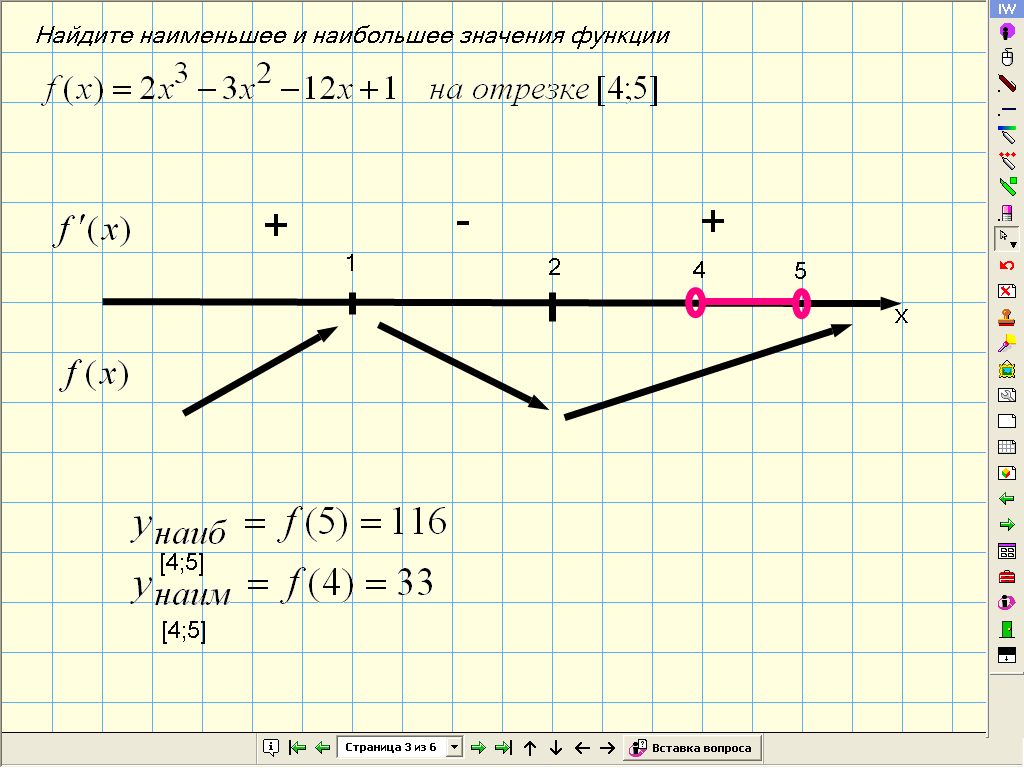
f(x) =2x3-3x2-12x+1 [4;5] Отличается ли оно от предыдущего? (стационарные и критические точки функции не принадлежат отрезку)
Итак, какая же ситуация возникла в этом примере? Оказалось, что на отрезке нет критических и стационарных точек. Что же это значит для функции. что она монотонна. На каких рисунках, на ваших листах, были монотонные функции? В каких точках достигались наибольшее и наименьшее значения. А значит достаточно узнать характер её монотонности, чтобы выяснить в какой точке она достигает наибольшего, а в какой наименьшего значения.
На интерактивной доске 2 способ решения (определить монотонность функции с помощью производной)
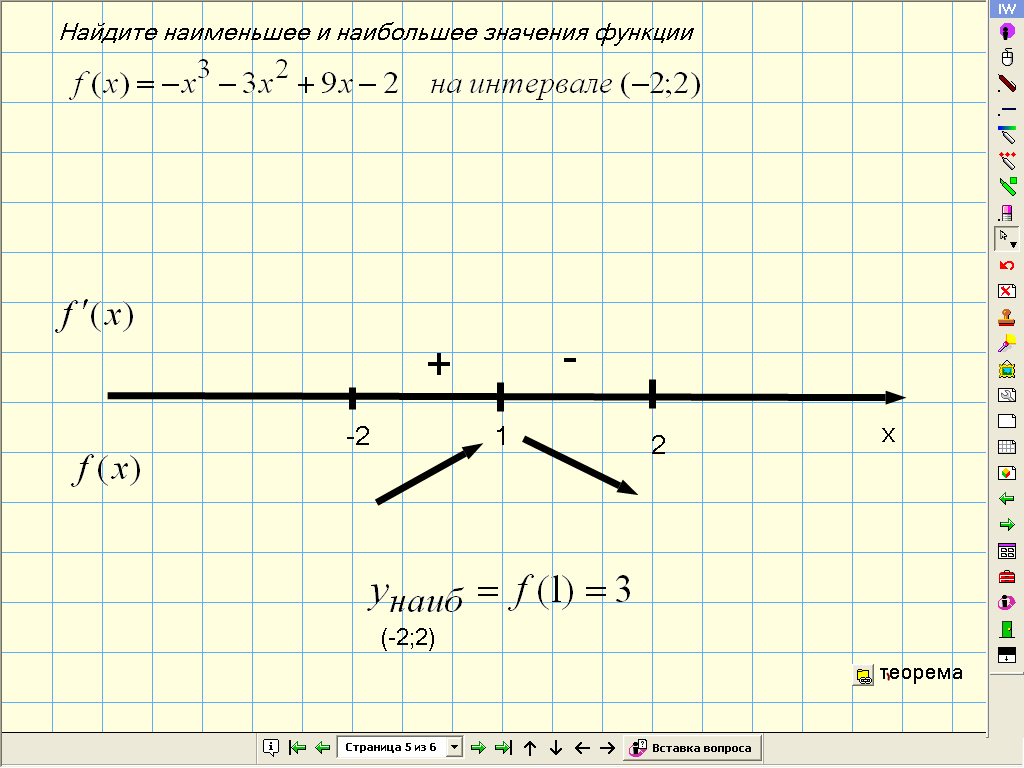
4. f(x) =-x3-3x2+9x-1 (-2;2) Учащиеся решают по алгоритму у доски.
Чем отличается этот пример от предыдущего? (одна точка принадлежит интервалу. Какие шаги алгоритма мы можем выполнить , какие нет? Как поступить? Что может помочь? ( Если учащиеся применят монотонность , то сразу перейти на теорему)На интерактивной доске 2 способ (с помощью промежутков монотонности функции )
Из этого способа следует
Если функция у=f(x), непрерывна на промежутке Х и имеет внутри него единственную стационарную или критическую точку х=х0, тогда:
А) если х=х0 – точка максимума, то унаиб= f(x0), ( рис 1)
Б) если х=х0 – точка минимума, то унаим= f(x0),(рис2)
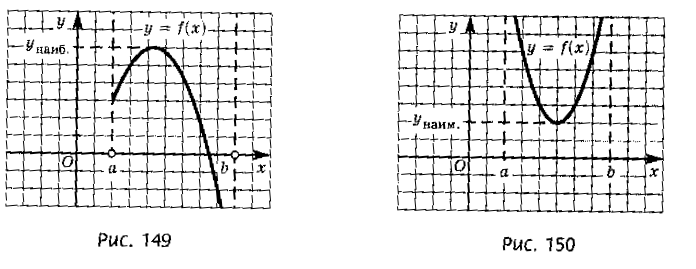
Рис 1 рис2
Вообще справедлива теорема ( смотреть учебник стр. 219-220).
3.Закрепление алгоритма № 32.8(а) – самостоятельно с помощью учителя
5.Итоги урока
Чем занимались на уроке?(Познакомились с новым видом задач на наибольшее и наименьшее значения функции)
Каков алгоритм решения этих задач? Какие частные случаи могут возникнуть? Что помогало на уроке?
6. Домашнее задание
Алгоритм, конспект, № 32.9(а.б) или рассмотреть пример 2, с. 218-219 – его особенности, план решения и решить №32.16(а)
7. Тестирование. ( Если останется время)
Вариант 1. 1. Найдите наименьшее значение функции на отрезке 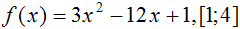
1) –8; 2) –11; 3) 12; 4) 8.
Вариант 2. 2. Найдите наибольшее значение функции на отрезке 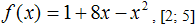
17; 2) 16; 3) 13; 4) 20.
Приложения.
Тема урока: «Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке»
Цель групповой работы: Сформулировать основные теоретические факты по теме, сформировать алгоритм решения задач на нахождение наибольшего и наименьшего значений непрерывной функции на промежутке.
Задание группам
1. Рассмотрите рисунки и ответьте на вопросы
Непрерывна ли функция на отрезке [a;b]?
Найдите стационарные и критические точки.
В какой точке достигается унаиб?
В какой точке достигается унаим?
| 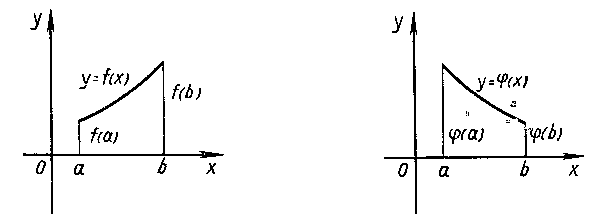
1) | 1) 2) 3) унаиб = f( ) 4) унаим= f( ) | 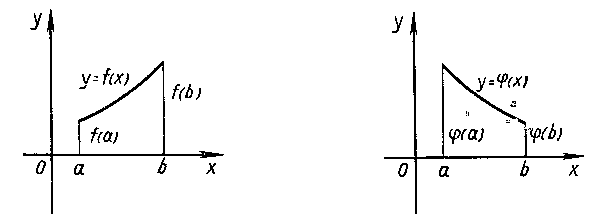
2) | 1) 2) 3) унаиб = ( ) 4) унаим= ( ) |
| 
3) | 1) 2) 3) унаиб = f( ) 4) унаим= f( ) |   4)           | 1) 2) 3) унаиб = f( ) 4) унаим= f( ) |
|  
5)     | 1) 2) 3) унаиб = h( ) 4) унаим= h( ) |  
6)      | 1) 2) 3) унаиб = g( ) 4) унаим= g( ) |
2. Сделайте выводы:
А) В каких точках функция может принимать свое наибольшее и наименьшее значения?
_______________________________________________________________________
Б) Если наибольшее ( наименьшее) значения функции достигаются во внутренних точках отрезка [a;b], то какие это могут быть точки?
_______________________________________________________________________
В) Всегда ли непрерывная на отрезке [a;b] функция имеет и наименьшее и наибольшее значение?__________________________________________
3
Т
Е
О
Р
И
Я
. Закончите предложения. 1) Если функция непрерывна на отрезке, то она достигает на нем и своего _______________и своего___________________ значения.
2) Наименьшего и наибольшего значений непрерывная функция может достигать, как на ________________________, так и внутри него.
3) Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в ________________________ или _____________________ точке.
4. Ответьте на вопросы.
1) На каких рисунках функция не имеет стационарных и критических точек?_________________________________________________________________________________
2) Охарактеризуйте монотонность функций на этих рисунках. ______________________________________________________________________________________
3) В какой точке достигаются унаиб и унаим, если функция убывает на отрезке [a;b]?
______________________________________________________________________________________
4) В какой точке достигаются унаиб и унаим, если функция возрастает на отрезке [a;b]?
______________________________________________________________________________________
5. Закончите предложения.
Т
Е
О
Р
И
Я
Если функция y=f(x) не имеет на отрезке[a;b] критических и стационарных точек, тогда
а) если f´(x)0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( _______ конце промежутка), а наименьшее в точке а (__________ конце промежутка).
б) если f´(x) b) f(x) – убывает на [a;b], поэтому наибольшее значение на отрезке функция принимает в _________ (___________________), а наименьшее в _____________ (_______________________).
Что необходимо знать, чтобы найти унаиб и унаим, для функции на отрезке [a;b], если функция непрерывна на этом отрезке?
1)_____________________________________________________________________________________
2)_____________________________________________________________________________________
______________________________________________________________________________________
6. Сформулируйте алгоритм нахождения наибольшего и наименьшего значений функции на отрезке.
(запишите алгоритм).
АЛГОРИТМ
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
8
Т
Е
О
Р
И
Я
. Работайте по распечатке №2 «Задания для работы на уроке».
9. Теорема
Теорема: Если функция у=f(x)непрерывна на промежутке Х и имеет внутри него единственную стационарную или критическую точку х=х0, тогда:
а)_____________________________________________________________________________________
б)_____________________________________________________________________________________
Распечатка №2
Задания для работы на уроке
1. Рассмотрите образец решения задачи и выделите шаги его решения.
Решите задания в тетради.
1. Найдите наибольшее и наименьшее значения функции f(x) =x4-2x2-3 на отрезке [0;2] .
2. Найдите наибольшее и наименьшее значения функции f(x) = 2x3-3x2-12х+1 на отрезке [4;5] .
3. Найдите наибольшее и наименьшее значения функции f(x) =-x3-3x2+9х-2 на интервале(-2;2) . Вернитесь к заданиям в парах к пункту 9.
4. Решите самостоятельно № 32.8(а).
5. Проверьте и оцените свою работу.
Домашнее задание
Алгоритм, конспект, № 32.9(а.б) или рассмотреть пример 2, с. 218-219 – его особенности, план решения и решить №32.16(а)