8 класс Алгебра Урок №35
Тема: Основное свойство алгебраической дроби. Сокращение дробей.
Цель: изучение основного свойство алгебраической дроби.
Задачи:
Образовательные: изучить основное свойство алгебраической дроби; рассмотреть примеры сокращения алгебраических дробей; практиковаться в приведении дробей к общему знаменателю.
Развивающие: развивать память и познавательный интерес к предмету.
Воспитательные: воспитание аккуратности и дисциплины, ответственного отношения к учёбе.
Автор разработки: Попов Дмитрий Сергеевич.
ХОД УРОКА
I. Организационный момент
Отдых наш кончается,
Работа начинается.
Усердно будем мы трудиться,
Чтобы чему-то научиться.
Проверка готовности к проведению урока.
II. Проверка выполнения домашнего задания
Проходит проверка выполнения домашнего задания. Те задания, которые вызвали затруднения в выполнении, учитель решает на доске с комментированием действий.
III. Постановка темы и целей урока
- Ребята, все вы, когда изучали в 5 классе главу «Обыкновенные дроби», рассматривали тему «Сокращения дробей». В ней вы работали с основным свойством дроби. Сегодня мы с вами должны разобраться, что называют основным свойством алгебраической дроби и будем практиковаться в сокращении дробей. Откройте тетрадь, запишите дату и тему урока «Основное свойство алгебраической дроби. Сокращение дробей».
IV. Изучение нового материала
- Давайте вспомним основное свойство обыкновенной дроби:
Значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
Напоминаю вам, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется сокращением.
На словах разобраться в теме хорошо, но давайте рассмотрим это на примерах.
Например, 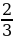 =
=  =
= 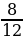 ,
, 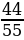 =
= 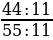 =
= 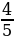 , при этом значение дроби не изменится.
, при этом значение дроби не изменится.
Теперь давайте вспомним определение алгебраической дроби:
Алгебраическая (рациональная) дробь – дробное выражение вида 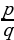 , где p и q ≠ 0 – многочлены.
, где p и q ≠ 0 – многочлены.
Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей и над ними можно проводить те же операции, что и над обыкновенными дробями.
Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля. Это будет тождественное преобразование алгебраической дроби. Вспомним, что как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.
Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.
Рассмотрим несколько примеров сокращения алгебраических дробей:
1) 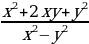 =
=  =
= 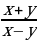 ;
;
2)  =
= 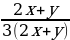 =
=  ;
;
3) 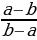 =
= 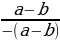 =
= 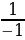 =
= 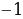 ;
;
4)  =
= 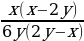 =
=  =
= 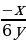 .
.
Алгебраические дроби также можно приводить к общему знаменателю. Давайте выполним задание вместе. А задание выглядит так:
Привести к общему знаменателю дроби а) 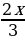 и
и  , б)
, б)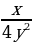 и
и  .
.
а) 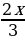 =
= 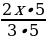 =
= 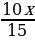 ;
;  =
= 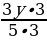 =
=  .
.
б) 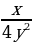 =
=  =
= 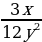
 =
=  =
= 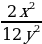 .
.
V. Закрепление изученного материала
Решение упражнений по учебнику: №24, №27, №30, №32, №34.
VI. Анонс домашнего задания
-
Прочитать п. 2 (§ 1)
-
Решить №23, №29 (а,в,г,е).
VII. Подведение итогов урока
- На данном уроке мы изучили основное свойство алгебраической дроби и рассмотрели основные задачи с его использованием. На следующем уроке мы более подробно разберем приведение дробей к общему знаменателю с использованием формул сокращенного умножения и метода группировки при разложении на множители.
Далее называю оценки за работу на уроке.
- До новых встреч!







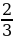 =
=  =
= 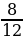 ,
, 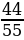 =
= 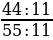 =
= 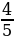 , при этом значение дроби не изменится.
, при этом значение дроби не изменится.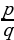 , где p и q ≠ 0 – многочлены.
, где p и q ≠ 0 – многочлены.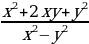 =
=  =
= 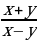 ;
; =
= 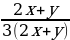 =
=  ;
;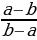 =
= 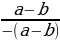 =
= 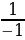 =
= 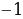 ;
; =
= 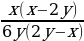 =
=  =
= 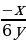 .
.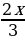 и
и  , б)
, б)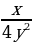 и
и  .
.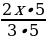 =
= 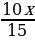 ;
; 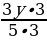 =
=  .
. =
= 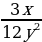
 =
= 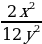 .
.


















