Конспект урока на тему: «Разложение вектора по двум неколлинеарным векторам

Геометрия

Тема: Разложение вектора по двум неколлинеарным векторам

Класс: 9 класс

Тип урока – урок изучения нового материала

Цели урока:

обучающие:

• познакомиться с понятием координаты вектора,

• изучить правила нахождения координат суммы и разности векторов, координат произведения вектора на число;

• научить применять знания при решении геометрических задач;

развивающие:

• формировать у учащихся таких приемов мышления и мыслительных операций как сравнение и аналогия, обобщение и конкретизация, умение делать логические выводы;

воспитательные:

• воспитывать интерес к изучению математических дисциплин

• воспитывать самостоятельность и ответственность.

Задачи урока:

• способствовать формированию умений раскладывать вектор по двум данным неколлинеарным векторам и нахождению координат вектора.

Формы работы: фронтальная.
Методы обучения: словесный, наглядный, практический.

Оборудование: компьютер, проектор, презентация Microsoft Office PowerPoint.

Учебник: Геометрия 9 класс, Л. С. Атанасян

УУД:
Регулятивные:
- планирование, контролирование и выполнение действий по образцу, владение навыками самоконтроля
Познавательные:
-умение пользоваться формулами разложения векторов.
Коммуникативные:
-самостоятельная деятельность, сотрудничество с учителем

Учащиеся должны:

Знать формулировку и доказательство леммы о коллинеарных векторах и теорему о разложении по двум неколлинеарным векторам;

Уметь решать задачи, применяя полученные знания.

Ход урока.

Актуализация знаний.

Учитель: Вам уже хорошо знакомо понятие вектора, и вы умеете выполнять некоторые действия над векторами. А именно: складывать, вычитать и умножать вектор на число.

Учитель: Что же такое вектор?

Ученик: Отрезок, для которого указанно, какая из его граничных точек считается началом, а какая – концом.

Учитель: Какие векторы называют коллинеарными?

Ученик: Это нулевые векторы, которые лежат либо на одной прямой, либо на параллельных прямых

Изучение нового материала.

Учитель: На этом уроке мы приступаем к более глубокому изучению вопроса о векторах и для начала запишем лемму о коллинеарных векторах.

Учитель: Лемма, а что же это такое? Леммой называется вспомогательная теорема, с помощью которой доказывается следующая теорема или несколько теорем. Лемма - доказанное утверждение. (показ презентации)

Лемма. Если векторы 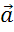 и 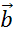 коллинеарны и  , то существует такое число , что .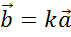

Доказательство.

1. 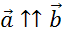  (соноправленные векторы, их направление совпадают)

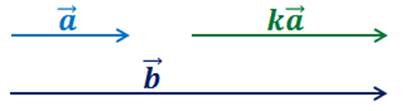
Пусть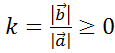 , тогда .

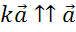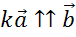
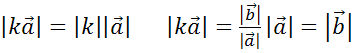
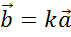
2. 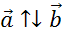(противоположно направленные векторы, их направления противоположны)

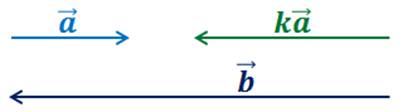
Пусть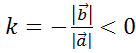 , тогда .

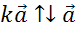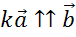
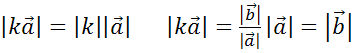
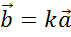
Лемма доказана.

Выполним задание. (показ презентации)

Выразить коллинеарные векторы 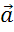, , 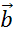, , 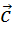 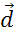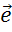и  через коллинеарный им вектор .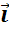

Решение.

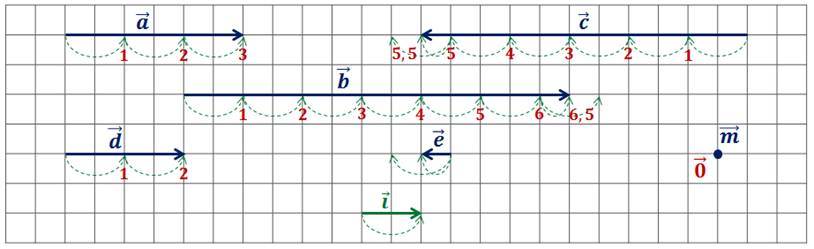
Итак, начнём с вектора 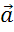 Видим, что векторы 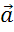и 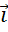 сонаправлены. Значит, k0.

Также, взяв длину вектора 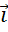 за единицу, видим что длина вектора  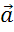в 3 раза больше.

Можем записать, что вектор 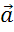 равен произведению вектора  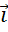на число 3.

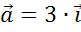
Рассмотрим следующий вектор, вектор 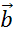. Он так же сонаправлен с вектором 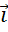, поэтому k0. При этом длина вектора  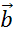в 6,5 раза больше длины вектора .

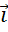Тогда вектор 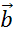 равен произведению вектора  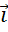на 6,5.

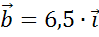
Далее рассмотрим вектор .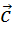

Он противоположно направлен с вектором 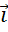. Поэтому k  в 5,5 раза больше длины вектора 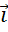. Тогда вектор .

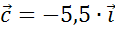Далее не сложно записать, что вектор .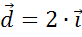

Следующим рассмотрим вектор 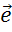. Он противоположно направлен вектору  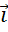и его длина в 2 раза меньше, поэтому вектор .

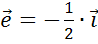Остался вектор 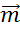. Как видите, он нулевой. Нам известно, что нулевой вектор сонаправлен любому вектору. И его длина равна нулю. Поэтому вектор .

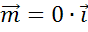Сейчас вспомним правило параллелограмма сложения двух векторов.

Если векторы-слагаемые 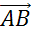 и 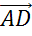  отложены от одной точки, то, построив на них параллелограмм ABCD, мы получим вектор  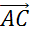их суммы.

Обозначим вектор 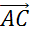  как вектор 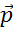. Он равен сумме .

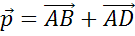В свою очередь вектор 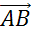 всегда можно выразить как произведение коллинеарного ему вектора  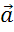на некоторое число x, а вектор  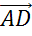— как произведение коллинеарного ему вектора на некоторое число y.

Тогда можно записать, что вектор .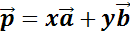

В таком случае говорят, что Вектор 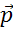 разложен по неколлинеарным векторам  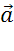и . 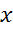, 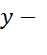коэффициенты разложения.

Теорема. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

Доказательство.

Пусть данными векторами будут неколлинеарные векторы 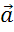 и .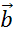

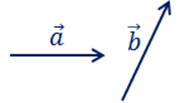
Докажем, что любой вектор 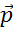 можно разложить по данным векторам.

1.

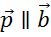
В этом случае по лемме о двух коллинеарных векторах получаем, что вектор
.

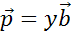Так же можно записать его разложение по векторам 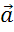 и 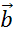. Только коэффициент разложения при векторе  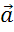будет равен нулю .

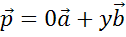2.

Отметим некоторую точку О и отложим от неё векторы 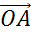,  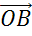и 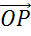, равные векторам 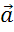,  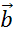и 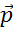 соответственно.

Через точку P проведём прямую параллельную прямой 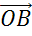. Точку пересечения полученной прямой с ОА обозначим как А₁.

По правилу треугольника вектор 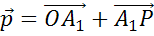. Вектор  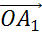коллинеарен вектору 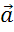, вектор  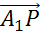коллинеарен вектору 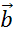. Это значит, что вектор 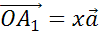, а вектор .

Отсюда получаем, что вектор 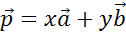. Тем самым мы разложили его по векторам  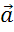и .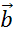

Действительно, на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам.

Теперь докажем, что коэффициенты разложения x и y определяются единственным способом.

Допустим, что кроме разложения 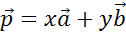 возможно другое разложение, .

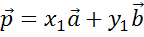Вычтем второе равенство из первого.

Получаем, что нулевой вектор можно разложить по векторам 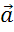 и 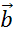, при этом коэффициенты разложения равны  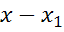и .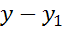

.

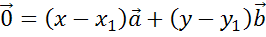Такое возможно только в том случае, если данные коэффициенты разложения равны нулю. А значит, при  и .

Значит, коэффициенты разложения определяются единственным способом.

Что и требовалось доказать.

.

Задания в класе: №911(а,б), №912(а,б,в), №916(а,б,в).

Подведём итоги урока.

Сегодня вы узнали, что любой вектор можно выразить через коллинеарный ему вектор умножением на некоторое число k.

Также мы рассмотрели примеры и убедились в том, что на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

Д/з: №911(в,г), №912 (г-и), №916(г)