Конспект урока "Несовместные события. Формула сложения вероятностей" (8 класс)

8 класс

Вероятность и статистика

Тема Несовместные события. Формула сложения вероятностей.

Здравствуйте, ребята!

Формула сложения вероятностей говорит, как вычислить вероятность объединения двух событий A и B, если известны вероятности этих событий и вероятность их пересечения:

P(A ∪ B) = P(A) + P(B) − P(A ∩ B)

Правило суммы для совместных событий: чтобы найти вероятность объединения двух совместных событий, нужно из суммы их вероятностей вычесть вероятность их пересечения.

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

Если события A и B не пересекаются, то формула сложения вероятностей принимает более простой вид: P(A ∪ B) = P(A) + P(B)

Правило суммы для несовместных событий: вероятность объединения несовместных событий равна сумме вероятностей каждого события.

P(A ∪ B) = P(A) + P(B)

Пример 1. Компания предлагает пользователям индивидуальную и семейную подписку на кино и музыку. Известно, что какая-либо подписка есть у клиентов. Сколько клиентов компании не имеют никакой подписки?

Решение. Всех клиентов компании можно поделить на три группы:

● A — есть индивидуальная подписка;
● B — есть семейная подписка;
● C — нет подписки.

В совокупности они образуют полную группу событий. Тогда P(A) + P(B) + P(C) = 1.

Известно, что клиентов с подпиской 60%, то есть ^{P(A ∪ B) = 0.6 = P(A) + P(B).}
Подставляя в формулу выше, получаем ^{P(C) = 0.4 = 40%} клиентов без подписки.

Пример 2

В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.

Решение. Примем, что событие А – «взят красный мячик», а событие В – «взят синий мячик». Тогда событие 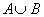 - «взят цветной (не белый) мячик». Найдём вероятность события А:

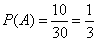
и события В:

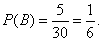
События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:

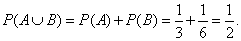
Пример 3.

Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.

Решение: Найдём вероятность того, что стрелок попадёт в цель:

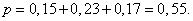
Найдём вероятность того, что стрелок попадёт мимо цели:

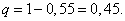
Пример 4.

Студент отправляется на экзамен. Вероятности получить 5, 4, 3 и 2 равны, соответственно, 0,1; 0,2; 0,3 и 0,4. Какова вероятность, что студент получит оценку не ниже четверки?

Решение. случайное  событие А  =( он получит 5),       В =(  он получит 4). Событие, что студент получит за экзамен не ниже четверки, есть сумма двух несовместных событий. По формуле вероятности суммы нескольких несовместных событий получим:

Р  = Р (А) + Р (В) =0,1+0,2=0,3 .

Ответ: 0,3

Пример 5.

Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение.

Обозначим через А событие «чайник прослужит меньше двух лет, но больше года», через В событие «чайник прослужит не меньше двух лет». События А и В несовместны. Событие С «чайник прослужит больше года» является их суммой C = A + B .

Из условия задачи следует, что вероятности P(B) = 0,89 и P(C)=0,97 . По формуле сложения вероятностей несовместных событий имеем Р(C) = P(A) + P(B) или

0,97 = P(A)+ 0,89 . Отсюда Р(A) =0.97-0,89=0,08.

Ответ: 0,08.

Пример 6.

На тарелке 12 пирожков: 3 с мясом, 6 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней или капустой.

Решение:

Обозначим через А событие «пирожок окажется с вишней», через В событие «пирожок окажется с капустой». Событие С «пирожок окажется с вишней или капустой» является их суммой С=А+В.

Всего 12 пирожков из них 3 с вишней, тогда Р(А)=3/12=0,25

Всего 12 пирожков из них 6 с капустой, тогда Р(В) =6/12=0,5

По формуле сложения вероятностей Р(С)=Р(А)+Р(В)

Р(С)=0,25+0,5=0,75

Ответ: 0,75.

Пример 7.

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется хотя бы в одном автомате.

Решение:

Обозначим через А событие «кофе закончится в первом автомате», через В событие «кофе закончится во втором автомате». Событие С «кофе закончится хотя бы в одном автомате» является их суммой C = A + B . Из условия задачи известны вероятности P(A) = P(B) = 0,35.

По формуле сложения вероятностей имеем: Р(С)=Р(А)+Р(В)

Р(С)=0,35+0,35=0,7

Значит, вероятность противоположного события «кофе останется хотя бы в одном автомате» равна 1-0,7=0,3.

Ответ: 0,3.

Домашнее задание. Повторите материалы темы. Выполните задания.

1. На карточках написаны натуральные числа от 1 до 10 включительно, после чего карточки перевернули и перемешали. Затем наугад открыли одну карточку. Какова вероятность того, что на ней будет написано простое число или число, большее 7?

2. Человек купил лотерейный билет. Вероятность выиграть 1000 рублей составляет 0,05; 500 рублей — 0,03; 200 рублей — 0,01. Какова вероятность хотя бы одного из этих выигрышей?