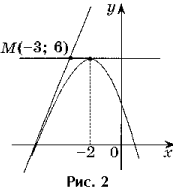06.11.19
Конспект урока алгебры по теме "Уравнение касательной"
Класс: 11
Тип урока: изучение нового материала.
Методы обучения: технология развивающего обучения, проблемный метод, контроля и взаимоконтроля, наглядный, частично-поисковый.
Цель урока:
Осознание понятия касательной к графику функции в точке, геометрического смысла производной.
Вывод уравнения касательной; составление алгоритма уравнения касательной к графику функции у = f (x).
Рассмотрение трех типов задач на нахождение уравнения касательной к графику функции.
Отработка навыка в составлении уравнения касательной в различных математических ситуациях.
Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
Выработка коммуникативных навыков в работе, развитие самостоятельной деятельности учащихся.
Задачи урока:
Отработать умения и навыки по применению производной;
Расширять кругозор; развивать математическую речь, внимание, скорость, память, логическое мышление.
Развивать умения анализировать, обобщать, показывать, использовать элементы исследования.
Развивать навыки исследовательской работы.
Ход урока.
1. Организационный момент
Проверка готовности учащихся к уроку. Сообщение темы урока.
2. Мотивация учащихся
Пусть слова, которые вы видите на экране, станут девизом сегодняшнего урока.
Плохих идей не бывает
Мыслите творчески
Рискуйте
Чтобы настроиться на урок повторим ранее изученный материал. Внимание на экран.
3. Актуализация знаний.
Давайте обсудим, что такое касательная к графику функции?
Согласны ли вы с утверждением, что «Касательная – это прямая, имеющая с данной кривой одну общую точку»?
Давайте рассмотрим конкретные примеры:
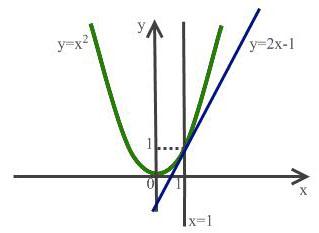
1) Прямая x = 1 имеет с параболой y = одну общую точку (1; 1), однако не является касательной к параболе.
Прямая же y = 2x – 1, проходящая через ту же точку, является касательной к данной параболе.
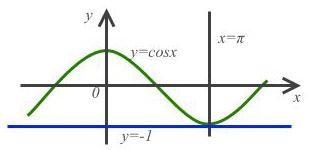
2) Прямая x = π не является касательной к графику y = cos x, хотя имеет с ним единственную общую точку (π; 1). С другой стороны, прямая y = - 1, проходящая через ту же точку, является касательной к графику, хотя имеет с ним бесконечно много общих точек вида (π+2 πk; 1), где k – целое число, в каждой из которых она касается графика.
После обсуждения, учащиеся приходят к выводу, что данное определение неверно.
Попробуйте сами сформулировать цель урока.
На данном уроке, мы с вами должны понять, что же такое касательная к графику функции в точке, как составить уравнение касательной и рассмотреть основные задачи на составление уравнения касательной.
4. Изучение нового материала
Посмотрите, чем отличается положение прямой х=1 от положения у=2х-1?
Сделайте вывод, что же такое касательная?
Чтобы задать уравнение прямой на плоскости, нам достаточно знать угловой коэффициент и координаты одной точки.
Начнём с углового коэффициента
Примем за определение: касательная — это предельное положение секущей.
Говорят, что касательная есть предельное положение секущей при ∆х → 0.
Существование производной функции в точке x0 эквивалентно существованию (невертикальной) касательной в точке (x0, f(x0)) графика, при этом угловой коэффициент касательной равен f '(x0) . В этом состоит геометрический смысл производной.
Определение касательной (записать в тетради)
Касательная к графику дифференцируемой в точке х0 функции у = f(х) — это прямая, проходящая через точку (x0, f(x0)) и имеющая угловой коэффициент f '(х0).
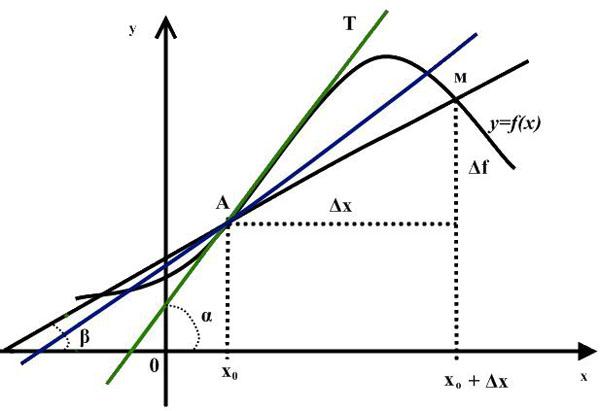
Проведем касательные к графику функции y = f(x) в точках х1, х2, х3, и отметим углы, которые они образуют с положительным направлением оси Ох.
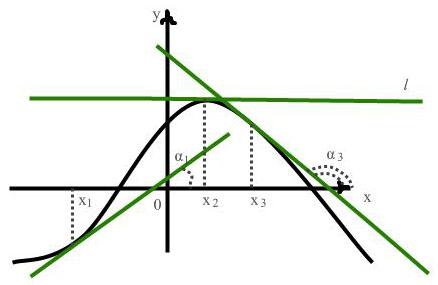
Мы видим, что угол α1 острый, угол α3 тупой, а угол α2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого - отрицателен. Поэтому
f '(х1)0, f '(х2) = 0, f '(х3)
Раз касательная — это прямая линия, а нам нужно составить уравнение касательной, то, что, как вы думаете, нам нужно вспомнить?
Вспомнить общий вид уравнения прямой. (у= кх+b)
Как еще называют число к? (угловой коэффициент или тангенс угла между этой прямой и положительным направлением оси Ох) к = tg α
В чем заключается геометрический смысл производной?
Тангенс угла наклона между касательной и положительным направлением оси оХ
То есть я могу записать tg α = yˈ(x0).
Давайте проиллюстрируем это на чертеже.
Пусть дана функция y = f (x) и точка М, принадлежащая графику этой функции. Давайте определим её координаты следующим образом: х= x0, у= f (x0), т.е. М (x0, f (x0)) и пусть существует производная f '(x0), т.е. в данной точке производная определена. Проведем через точку М касательную.
Уравнение касательной – это уравнение прямой, поэтому оно имеет вид: y = kx + b. Следовательно, задача состоит в том, чтобы отыскать k и b. Обратите внимание на доску, из того, что там записано, можно ли найти к? (да, k = f '(x0).)
Как теперь найти b? Искомая прямая походит через точку М x0 (; f (x0)), подставим эти координаты в уравнение прямой: f(x0) = k x0 +b , отсюда b = f(x0) – k x0,
т. к. к = tg α= yˈ(x), то b = f(x0) – f '(x0) x0
Подставим значение b и к в уравнение y = kx + b.
y = f '(x0)x + f(x0) – f '(x0) x0, вынося за скобку общий множитель, получаем:
y = f(x0) + f '(x0) · (x- x0).
Нами получено уравнение касательной к графику функции y = f(x) в точке х = x0.
Уравнение касательной к графику функции f в точке М(x0, f(x0)) имеет вид:
y = f '(х0)(x - x0) + f(x0)
Чтобы уверенно решать задачи на касательную, нужно четко понимать смысл каждого элемента в данном уравнении. Давайте ещё раз остановимся на этом:
1. (x0, f (x0 )) – координаты точки касания
2. f '(x0) = tg α = к - тангенс угла наклона или угловой коэффициент
3. (х,у) – координаты любой точки касательной
И так мы вывели уравнение касательной, проанализировали смысл каждого элемента в данном уравнении. Зная эту формулу, не нужно каждый раз заново проводить рассуждения по отысканию уравнения касательной. Надо просто найти входящие в неё значения f (х0) и f'(х0) и подставить их.
Давайте попробуем теперь вывести алгоритм составления уравнения касательной к графику функции y = f (x).
Предлагаю составить алгоритм самим учащимся.
Алгоритм нахождения уравнения касательной в точке (записать в тетради)
1.Найти производную функции
2.Найти значение функции в точке касания
3.Найти значение производной в точке касания
4. Подставить найденные значения в общее уравнение касательной.
(Раздаю учащимся напечатанный заранее алгоритм как памятку для последующей работы.)
5. Первичное закрепление изученного материала
Есть три основных типа задач на составление уравнения касательной.
1. Дана абсцисса точки касания х0.
2. Дан угловой коэффициент наклона касательной, то есть значение производной функции в точке х0.
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
Пример 1. Составить уравнение касательной к графику функции f(x) = х² - 3х + 5 в точке с абсциссой х0 = -1.
Решение:
Составим уравнение касательной (по алгоритму).
(х0) = -1;
f(х0) = f(-1) = 1 + 3 + 5 = 9;
f '(х0) = 2х – 3,
f '(х0) = f '(-1) = -2 – 3 = -5;
y = 9 – 5 · (x + 1), y = 4 – 5x.
Ответ: y = 4 – 5x.
Пример 2. Дана функция f(x)=+3-2x-2. Напишите уравнение касательной к графику функции y=f(x), параллельной прямой y=-2x+1.
Решение. Производная данной функции существует для любого х из R. Найдем ее:
(f(x))' = (+3 - 2x - 2) = 3 + 6x - 2.
Поскольку касательная параллельна y = -2x + 1, получим уравнение:
3 + 6x - 2 = -2;
x + 2x = 0;
x ∙ (x + 2) = 0;
= 0; = -2.
Подставим и в уравнение функции и найдем и .
= (1 + 3 - 2 - 2) = 0;
= (-8 + 12 + 4 - 2) = 6.
Подставляем найденные координаты в уравнение касательной и вычислив, получим:
y = -2x; y = -2x +10.
Ответ: y = -2x; y = -2x +10.
Пример 3. Напишите уравнения всех касательных к графику функции y = – x2 – 4x + 2, проходящих через точку M(– 3; 6).
Решение. Точка M(– 3; 6) не принадлежит графику функции, так как f(– 3) ≠ 6
х0 – абсцисса точки касания. f(х0) = – х02 – 4 х0 + 2.
Производная данной функции существует для любого х из R. Найдем ее: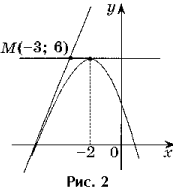
f '(x) = – 2x – 4, f '(х0) = – 2 х0 – 4.
4. y = – у=х0 2 – 4 х0 + 2 – 2(х0 + 2)( х0 – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – х02 – 4 х0 + 2 – 2(х0 + 2)(– 3 – х0 ),
х02 + 6 х0 + 8 = 0; х0 1 = – 4, х02 = – 2. Это значит, что через точку М можно провести две касательные к графику функции.
Если х0 = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если х0 = – 2, то уравнение касательной имеет вид y = 6.
Ответ: y = 4x + 18; y = 6
6. Физкультминутка. Упражнение “Роняем руки” расслабляет мышцы всего корпуса. Дети поднимают руки в стороны и слегка наклоняются вперёд. По команде учителя снимают напряжение в спине, шее и плечах. Корпус, голова и руки падают вниз, колени слегка подгибаются. Затем дети выпрямляются, последовательно разгибаясь в тазобедренном, поясничном и плечевом поясе, и принимают исходное положение. Упражнение повторить несколько раз.
7. Самостоятельная работа с самопроверкой на уроке.
Напишите уравнение касательной к графику функции у=f(x) в точке с абсциссой а.
Вариант 1 Вариант 2
f(x) = х²+ х+1, а=1 f(x)= х-3х², а=2
Ответы: 1 вариант: у=3х; 2 вариант: у= -11х+12
8. Подведение итогов урока.
- что называется касательной к графику функции в точке?
- в чём заключается геометрический смысл производной?
- сформулируйте алгоритм нахождения уравнения касательной в точке.
9. Домашнее задание. П.5.2; № 5.21; №5.35; Подготовка к ЕГЭ В-8 № 3 - 10
10. Рефлексия деятельности на уроке.
Что нового узнали на уроке?
Что было наиболее сложным для понимания?