Конспект урока по астрономии "Законы движения планет" для 11 класса

Законы движения планет – законы Кеплера

Гелиоцентрическая система Н. Коперника.

Планеты движутся по круговым орбитам (считалось с древнейших времён – по окружности).

Планеты движутся равномерно.

Но между предвычисленным и наблюдаемым положением планет существовало различие - это выявил австрийский астроном – основоположник теоретической астрономии ИОГАН КЕПЛЕР (27.12.1571 – 15.11.1630).

Он впервые решился пересмотреть причины движения планет вокруг Солнца, Луны вокруг Земли. Он ошибался в оценке природы притягивающей силы, но догадывался, что Солнце искажает притяжением пути планет, которые стремятся двигаться по прямой.

 Работая в Праге учеником у Тихо Браге (1546-1601, Дания) он унаследовал результатов кропотливых и многолетних наблюдений Тихо Браге за планетой Марс - подробные таблицы наблюдения движения Марса и на их основе (этих данных) вывел законы движения планет (но не объяснил их т.к. не был открыт И. Ньютоном закон всемирного тяготения), преодолев предрассудки о равномерном движении по “самой совершенной” кривой - окружности. Открытие этих законов явилось важнейшим этапом в развитии гелиоцентризма.

Позднее, после открытия Ньютоном закона всемирного тяготения, законы Кеплера были выведены как точное решение задачи двух тел.

Открытые законы носят имя Кеплера.
Для построения орбиты планет (на примере Марса) Кеплер перейдя от экваториальной системы координат к системе координат, указывающих его положение в плоскости орбиты принял в приближении орбиту Земли окружностью. Для построения орбиты применил способ показанный на рисунке, отсчитывая прямое восхождение от точки весеннего равноденствия на положение нескольких противостояний Марса. Проведя по полученным точкам плавную кривую получил эллипс и нашел формулу описывающую орбиту планеты X=е*sin (а)+M.
 CD- "Red Shift 5.1" - нахождение сегодняшнего положения Марса и его характеристика по выведенным таблицам.

Эллипс- замкнутая кривая, у которой сумма расстояний от любой точки до фокусов постоянна (const).

Если расстояние F₁F₂ обозначить 2с, а длину веревки считать 2а, то в системе координат, где ось ОХ совпадает с линией F₁F₂, а начало совпадает с серединой отрезка F₁F₂, эллипс задается уравнением х² : а² + у² : в² = 1. Числа а и в задают размеры полуосей эллипса. Если а = в, то эллипс превращается в окружность.

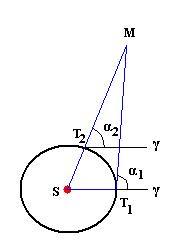
Форма эллипса (степень отличая от окружности -  “сплюснутость”) характеризуется эксцентриситетом: е=с/а (форм.14), где а большая полуось орбиты, а с=OF расстояние от центра эллипса до его фокуса.

 При е=с=0 эллипс превращается в окружность, а при е=1 в отрезок.

Приложение IХ.

Большая полуось орбиты Земли (среднее расстояние Земли от Солнца) - расстояние, принятое за астрономическую единицу. 1а.е.=149 597 868 ± 0,7 км ≈ 149,6 млн. км.  

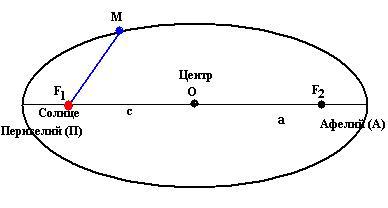
Для эллиптической орбиты планеты характерны относительно Солнца точки:

 Перигелий (греч. пери – возле, около) ближайшая к Солнцу точка орбиты планеты (для Земли 1-5 января). В перигелии  южное полушарие Земли получает солнечной энергии на 6% больше, чем северное полушарие.

Афелий (греч. апо – вдали) наиболее удаленная от Солнца точка орбиты планеты (для Земли 1-6 июля).

Учитывая греческие названия планет, характерные точки эллиптической орбиты ее спутников будут иметь собственные названия. Так Луна – Селена (переселений, апоселений), Земля – Гея (перигей, апогей).

Называют законом площадей.

Заштрихованные площади фигур равны за равные промежутки времени. Из чертежа дуги разные, отсюда υ_пυ_а, т.е в перигелии υ_max, а в афелии υ_min.

По закону сохранения энергии полная механическая энергия замкнутой системы, между которыми действует сила тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергии планеты неизменна во всех точках орбиты. По мере приближения к Солнцу кинетическая энергия планеты возрастает а ее потенциальная энергии уменьшается.

     В соответствии со вторым законом Кеплера, орбитальная скорость обратно пропорциональна радиус-вектору. Поэтому скорость движения Земли по орбите также не постоянна, а изменяется от 29,5 км/с в афелии (июль) до 30,3 км/с в перигелии (январь). Соответственно, и расстояние от осеннего до весеннего равноденствия на орбите Земля проходит быстрее, чем противоположную, летнюю часть, а весна и лето в Северном полушарии на 6 суток продолжительнее осени и зимы. Например, Земля проходила точку перигелия, ближайшую к Солнцу, в 1998 году 04 января в 21 часов 15 минут 1 секунду всемирного времени UT. При этом ее расстояние от Солнца составляло 147099552 км. Противоположную точку орбиты, афелий, Земля проходила 3 июля 1998 года в 23 часа 50 минут 11 секунд всемирного времени UT. При этом Земля была от Солнца на расстоянии 152095605 км, т.е. на 5 миллионов километров больше. Это изменение расстояния до Солнца также хорошо заметно по изменению его видимого углового размера, который от 32´34" в январе уменьшается до 31´30" в июле.

Поток энергии от Солнца, падающий на Землю, изменяется обратно пропорционально квадрату расстояния. Поэтому зимы в северном полушарии менее суровые, чем в южном, а лето в северном полушарии более прохладное.

Законы Кеплера применимы не только для планет, но и к движению их естественных и искусственных спутников.