Конспект урока по геометрии 8 класс
Решение задач по теме: «Вписанный угол»
Задача урока: опираясь на ранее рассмотренный приём при доказательстве теоремы о вписанном угле, доказать новые утверждения об углах, связанных с окружностью.
Цели урока:
- образовательная: совершенствовать знания о центральном и вписанном углах; формировать умения применять их при решении задач; учить учащихся использовать известные приёмы доказательства при решении новых математических задач;
- развивающая: формировать приемы умственной деятельности: сравнения, аналогии, сопоставления; прививать навыки исследовательской деятельности; углублять знания по данной теме; развивать точную лаконичную речь;
- воспитательная: учить преодолевать трудности; воспитывать стремление к совершенствованию знаний.
Структура урока.
-сообщение учащимся цели предстоящей работы;
-воспроизведение учащимся знаний, которые потребуются для выполнения заданий;
-перенос приобретённых знаний и их первичное применение в новых условиях;
-самостоятельная работа;
-подведение итогов урока; задание на дом;
-выставление оценок за урок.
Ход урока.
-
Организационный момент.
Ребята, сегодня на уроке мы продолжим решение задач на применение понятий центрального и вписанного углов, а также попытаемся самостоятельно доказать новые утверждения об углах, связанных с окружностью, используя один из знакомых нам уже приёмов рассуждения.
Понятие угол и окружность появилось много веков назад. Инженеры и математики древности пользовались этими понятиями при расчётах различных архитектурных сооружений. Так же эти понятия использовались при навигации на море и на суше. В наше время понятие и свойство центральных и вписанных углов используется в науке и технике. Например, невозможно представить себе без этих понятий современную инженерную графику и машиностроение. Хочется ещё раз повторить народную мудрость "Ум без догадки - гроша не стоит", т.к. при решении геометрических задач нужна смекалка, умение рассуждать, анализировать, а это невозможно без знаний и вдохновения. Вдохновения нам на протяжении всего урока.
-
Устная работа.
Вначале вспомним определения и понятия, которые нам понадобятся на уроке для решения задач. Одним из домашних заданий было подготовить вопросы по теме «Центральные и вписанные углы».
Пока работаем устно, один из учеников подготовит домашнюю задачу №660 на доске.
-
Сформулируйте определение центрального угла. (Угол, с вершиной в центре окружности называется центральным углом).
-
Чему равна градусная мера центрального угла? (Градусная мера центрального угла равна градусной мере дуги на которую он опирается)
-
Сформулируйте определение вписанного угла. (Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом).
-
Сформулировать теорему о вписанном угле. (Вписанный угол измеряется половиной дуги, на которую он опирается.)
-
Сформулировать следствие 1. (Вписанные углы, опирающиеся на одну и ту же дугу, равны).
-
Сформулировать следствие 2.
(Вписанный угол, опирающийся на полуокружность – прямой).
-
Связь вписанного и центрального углов, опирающихся на одну и ту же дугу. (Центральный угол всегда в два раза больше вписанного, опирающегося на ту же дугу.)
-
Работа по заготовленным чертежам (презентация):
найти угол α.
-
Проверим решение домашней задачи № 660.
Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32. Большая дуга окружности, заключённая между сторонами этого угла, равна 100. Найдите меньшую дугу.
Р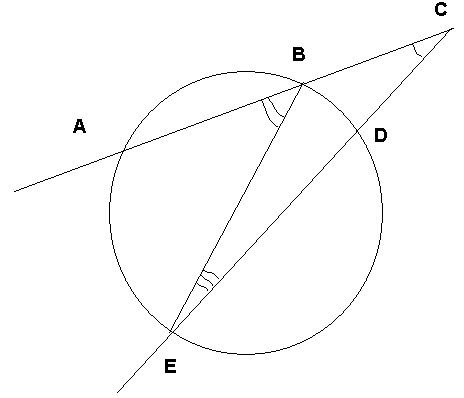
 ешение.
ешение.
-
Проведём ВЕ
-
Т.к. АВЕ – вписанный,
то АВЕ = 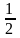 АЕ =
АЕ = 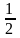 100 = 50.
100 = 50.
-
Т.к. АВЕ – внешний угол ВЕС,
то АВЕ = ВЕС + BCD,
откуда ВЕС = АВЕ - BCD,
ВЕС = 50 – 32 = 18.
-
Т.к. ВЕD = 18 – вписанный,
то ВЕD = 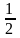 BD,
BD,
значит BD = 2 ВЕD = 2 18 = 36.
Ответ: BD = 36.
-
Решение задач с применением элементов исследовательской деятельности.
Вывод и доказательство утверждения о величине угла между двумя секущими.
Посмотрим внимательно на результат в задаче. Имеется ли связь между величиной угла и градусными мерами дуг, заключенных внутри угла?
Заметим, что (100 – 36) : 2 = 64 : 2 = 32.
Наводящие вопросы:
-
Как был образован угол АСЕ?
-
С помощью величин каких дуг мы нашли величину угла АСЕ?
-
Сформулируйте гипотезу о величине угла между двумя секущими.
Гипотеза:
1). Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей дуг, заключенных между его сторонами.
2). Угол, вершина которого лежит вне круга и стороны пересекаются с окружностью, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Т.е., нам надо доказать, что
АСЕ = 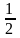 (АЕ - BD).
(АЕ - BD).
Доказательство: (доказывать у доски)
-
Т.к. АВЕ – вписанный в окружность, то АВЕ = 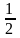 АЕ.
АЕ.
-
Т.к. BED - вписанный в окружность, то BED = 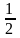 BD.
BD.
-
Рассмотрим ВЕС: АВЕ – внешний угол данного треугольника. Его величина равна сумме двух других углов треугольника, не смежных с ним. Значит,
АВЕ = ВЕС + ВСЕ,
ВСЕ = АВЕ - ВЕС,
ВСЕ = 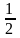 АЕ -
АЕ - 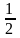 BD =
BD = 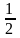 (АЕ - BD).
(АЕ - BD).
Итак,
Утверждение: Угол, образованный двумя секущими, выходящими из одной точки, измеряется полуразностью дуг, заключённых внутри угла.
Утверждение: Угол, вершина которого расположена вне круга, а каждая из сторон пересекает окружность в двух точках, измеряется полуразностью дуг, заключенных внутри угла.
Ребята, при доказательстве данного утверждения и решении домашней задачи какой метод доказательства мы использовали?
(Достраивали до треугольника и использовали свойство внешнего угла треугольника).
Применение: №661 (устно).
Решение: = (140 – 52) : 2 = 88 : 2 = 44.
Ответ: 44°.
Вывод и доказательство утверждения о величине угла между двумя пересекающимися хордами.
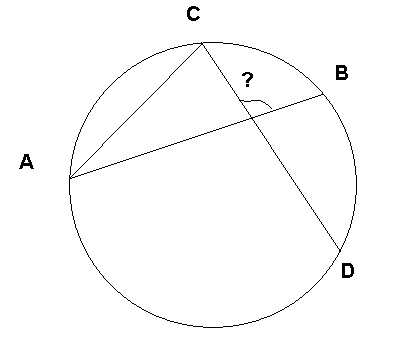
Ребята, мы рассмотрели угол с вершиной вне окружности. А что, если теперь нам рассмотреть угол внутри окружности, например ВЕС.
Можем продолжить стороны этого угла и
рассмотрим две пересекающиеся хорды окружности (рисунок на доске).
Наводящие вопросы:
1. Являются ли центральными или вписанными углы, образованные пересекающимися хордами?
2. Проведём хорду АС. Какие вписанные углы при этом получились?
3. Рассмотрим вписанные углы АСD и САВ:
АСD =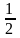 AD; САВ =
AD; САВ = 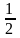 СВ.
СВ.
4. Неизвестный угол - внешний угол АСЕ, значит его величина равна сумме двух других углов треугольника, не смежных с ним:
= АСD + САВ = 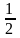 AD +
AD + 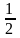 СВ =
СВ = 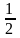 (AD + СВ).
(AD + СВ).
5. Сформулируйте гипотезу о величине угла между двумя пересекающимися хордами.
Гипотеза:
1). Угол между двумя пересекающимися хордами равен полусумме двух дуг, заключённых между этими хордами.
2). Угол с вершиной внутри круга измеряется полусуммой дуг, одна из которых расположена внутри этого угла, а другая – внутри угла, вертикального данному.
Применение: №662 (устно).
Решение:∠ВЕС = (54 + 70) : 2 = 124 : 2 = 64.
Ответ:64°
-
Подведение итогов урока:
Выставить оценки.
Какие новые утверждения об углах, связанных с окружностью, вы сегодня узнали? Как вы получили эти новые сведения?
-
Самостоятельная работа.
Литература:
-
Геометрия: Учеб.для 7 – 9 кл. общеобразоват. Учреждений/Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 10-е изд. – М.: Просвещение, 2010. – 388с.: ил.
-
Гаврилова Н.Ф. Универсальные поурочные разработки по геометрии: 8 класс. – 2-е изд., перераб. И доп. – М.: ВАКО, 2011. – 368 с. – (В помощь школьному учителю).
-
Александров А.Д. и др., Геометрия для 8 – 9 классов: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики/А.Д. Александров, А.Л. Зернер, В.И. Рыжик – М.: Просвещение, 1991. – 415 с.
-
Т.М. Мищенко, «Геометрия в таблицах. 7 – 9 классы», «АСТ. Астрель. Транзиткнига», Москва, 2005. – 40 с.
-
Е.М.Рабинович, «Математика. Задачи и упражнения на готовых чертежах. Геометрия. 7 – 9 классы», «Илекса», Москва – Харьков, 1998. – 64 с.
Интернет-ресурсы:
-
festival@1september.ru
-
uztest.ru/abstracts/?idabstract=98
-
berdov.com/ege/plane_geometry/circl...
|
ФИ ученика___________________
Вариант 1 1 N .      
 ![]() 


 М K
Найти:∠MNK Решение:
Ответ:
2. Дано: M  N : АС=1:5 N : АС=1:5  АМ=100° АМ=100°  NC=140° NC=140° Найти: ∠АВС
  М N A C В
Решение:
Ответ: |
ФИ ученика__________________
Вариант 2 -
О – центр окружности    655 5°
 O 300 0
  
A D
Найти:∠АОD Решение:
Ответ:
2.Дано: A  D : CB=4:6 D : CB=4:6  AC=80° AC=80°  BD=120° BD=120° Найти:∠АЕD   A C D B E
Решение:
Ответ: |
|
Вариант 1 1 N .      
 ![]() 


 М K
Найти:∠MNK
2. Дано: M  N : АС=1:5 N : АС=1:5  АМ=100° АМ=100°  NC=140° NC=140° Найти: ∠АВС
  М N A C В
|
Вариант 2 -
О – центр окружности    655 5°
 O 300 0
  
A D
Найти:∠АОD
2.Дано: A  D : CB=4:6 D : CB=4:6  AC=80° AC=80°  BD=120° BD=120° Найти:∠АЕD   A C D B E
|







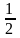 АЕ =
АЕ =