Квадратичная функция и ее график
Цель: познакомить учащихся с квадратичной функцией, ее графиком и свойствами.
Задачи:
Образовательная – актуализовать ранее полученные знания о функции и ее графике, дать определение квадратичной функции, сформулировать свойства.
Развивающая – развить навыки анализа и аналогии проведения исследования функции, развить грамотную математическую речь.
Воспитательная – воспитывать трудолюбие, умение выслушать, применять знания.
Тип урока: урок изучения нового материала.
План урока:
Организационный момент
Актуализация знаний
Изучение нового материала
Закрепление новых знаний
Подведение итогов урока
Информация о домашнем задании
Оборудование: доска, карточки с заданиями
Ход урока:
Организационный момент.
Актуализация знаний
Что такое функция?
Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Что является графиком функции?
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.
Какие графики вы уже изучили? ( ).
).
Индивидуально-групповая работа.
Изучение нового материала
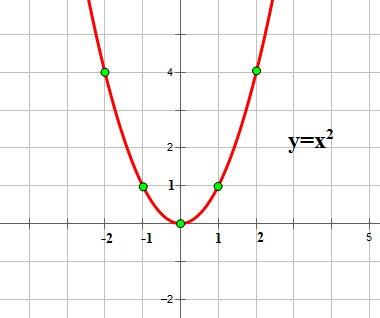
Рассмотрим квадратичную функцию  .
.

Мы получаем формулу вида  , где
, где  .Значит , график функции
.Значит , график функции есть парабола, которую можно получить из графика функции
есть парабола, которую можно получить из графика функции с помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у. Вершина параболы является точка
с помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у. Вершина параболы является точка  .
.
Квадратичной функцией называется функция, которую можно задать формулой вида  , где х - независимая переменная, a,b и c- некоторые числа, причем
, где х - независимая переменная, a,b и c- некоторые числа, причем  .
.
Если старший коэффициент a0, то ветви параболы направлены вверх.
Если старший коэффициент a
Алгоритм построения графика:
Определить направление ветвей параболы;
Найти координаты вершины параболы и отметить ее на координатной плоскости, определить ось симметрии параболы
Найти нули функции;
Если нулей функции нет, то определить точки пересечения с осью Оу, отметить ей симметричную.
Свойства функции  при
при  :
:
1. Ветви параболы направлены вверх.
2. Областью определений является множество действительных чисел.
3. Областью значений функции является промежуток  .
.
4. Функция возрастает в промежутке  и убывает на промежутке
и убывает на промежутке  .
.
5. Наименьшее значение функция принимает в точке  , наибольшего значения функция не имеет.
, наибольшего значения функция не имеет.
Свойства функции  при
при  :
:
1. Ветви параболы направлены вниз.
2. Областью определений является множество действительных чисел.
3. Областью значений функции является промежуток  .
.
4. Функция возрастает в промежутке  и убывает на промежутке
и убывает на промежутке  .
.
5. Наибольшее значение функция принимает в точке  , наименьшего значения функция не имеет.
, наименьшего значения функция не имеет.
Уравнение квадратичной функции имеет вид – в этом уравнении
– в этом уравнении  – координаты вершины параболы или в уравнении квадратичной функции
– координаты вершины параболы или в уравнении квадратичной функции
 , и второй коэффициент – четное число.
, и второй коэффициент – четное число.
Знаки функции.
Нули функции разбивают ее область определения на промежутки, на каждом из которых функция сохраняет постоянный знак.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции  с осью ОХ, нужно решить уравнение
с осью ОХ, нужно решить уравнение  .
.
В случае квадратичной функции  нужно решить квадратное уравнение
нужно решить квадратное уравнение  .
.
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения. И здесь возможны три случая:
, который определяет число корней квадратного уравнения. И здесь возможны три случая:
1. Если
 ,то уравнение
,то уравнение  не имеет решений, и, следовательно, квадратичная парабола
не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если
не имеет точек пересечения с осью ОХ. Если  ,то
,то
2. Если 
 ,то уравнение
,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола
имеет одно решение, и, следовательно, квадратичная парабола  имеет одну точку пересечения с осью ОХ, квадратичная функция обращается в нуль в одной точке
имеет одну точку пересечения с осью ОХ, квадратичная функция обращается в нуль в одной точке . числовая ось разбивается на два промежутка и , однако знак функции в этих промежутках один и тот же, зависящий от старшего коэффициента а.
. числовая ось разбивается на два промежутка и , однако знак функции в этих промежутках один и тот же, зависящий от старшего коэффициента а.
Если  , то
, то
3. Если  имеет два решения, и, следовательно, квадратичная парабола
имеет два решения, и, следовательно, квадратичная парабола  имеет две точки пересечения с осью ОХ:
имеет две точки пересечения с осью ОХ:
,
Если  , то
, то
Промежутки монотонности.
Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Теорема. Точка  делит числовую ось на два промежутка, на каждом из которых квадратичная функция монотонна. Характер монотонности зависит от знака старшего коэффициента a. При a 0 квадратичная функция убывает на промежутке (
делит числовую ось на два промежутка, на каждом из которых квадратичная функция монотонна. Характер монотонности зависит от знака старшего коэффициента a. При a 0 квадратичная функция убывает на промежутке ( ] и возрастает на промежутке [
] и возрастает на промежутке [ ).
).
Наибольшее и наименьшее значения.
Функция 
 , заданная на всей числовой оси, принимает в точке
, заданная на всей числовой оси, принимает в точке  свое наименьшее значение, равное
свое наименьшее значение, равное  . Наибольшего значения y не имеет. При a происходит обратное: при
. Наибольшего значения y не имеет. При a происходит обратное: при  y принимает наибольшее значение, а наименьшего значения у нее нет.
y принимает наибольшее значение, а наименьшего значения у нее нет.
Закрепление новых знаний.
Как видно из графика , он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Построим для примера график функции .
.
Вспомним линейные преобразования графиков функций. Чтобы построить график функции  , нужно сначала построить график функции
, нужно сначала построить график функции , затем ординаты всех точек графика умножить на 2, затем сдвинуть его вдоль оси ОХ на 1 единицу вправо, а затем вдоль оси OY на 4 единицы вверх:
, затем ординаты всех точек графика умножить на 2, затем сдвинуть его вдоль оси ОХ на 1 единицу вправо, а затем вдоль оси OY на 4 единицы вверх:
Примеры:
Используя шаблон параболы , постройте график функции:
, постройте график функции:
а) f(x)= x² - 3; б) f(x)= - x²+4; в) f (х) = (х-2)²; г) f(x) =(х-2)²-4.
| План исследования функции | Пример решения |
| 1. Определить вид функции, если возможно. | Дана функция вида  Графиком функции  является парабола, ветви которой направлены вверх, так как a0. является парабола, ветви которой направлены вверх, так как a0. |
| 2. Найти область определения функции. | D(y) (-∞;+∞) |
| 3. Найти область значения функции | E(y) (-4;+∞) |
| 4. Найти нули функции (точки пресечения с осью х), если возможно. | y=0,   x1=0 или x+4 =0 x2= - 4 |
| 5. Определить, при каких значениях аргумента х значения функции у0, при каких значениях аргумента у . | у0 при х у при х0 |
| 6. Определить, является ли функция возрастающей (убывающей) или указать промежутки возрастания (убывания). | Вершина параболы имеет координаты (-2; -4). Следовательно, функция убывает на промежутке (-∞; -2], возрастает на промежутке [-2; +∞) |
| 7. Начертить график.
| |
Подведение итогов урока.
Повторение определений.
Информация о домашнем задании.
Карточки с заданиями.
1.Построить график функции у= 0,5 (х-1)2 и описать ее свойства.
2.Определить область значений функций:
а)  ; б)
; б)  .
.
3.Построить график у=-2х2+8х-5, определить ООФ и найти наименьшее и наибольшее значение функции.
7






 ).
).
 .
.
 , где
, где  .Значит , график функции
.Значит , график функции с помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у. Вершина параболы является точка
с помощью двух параллельных переносов - сдвига вдоль оси х и сдвига вдоль оси у. Вершина параболы является точка  .
. .
. :
: .
. и убывает на промежутке
и убывает на промежутке  .
. , наибольшего значения функция не имеет.
, наибольшего значения функция не имеет.  :
: .
. – в этом уравнении
– в этом уравнении  – координаты вершины параболы или в уравнении квадратичной функции
– координаты вершины параболы или в уравнении квадратичной функции









