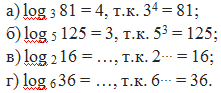Тема: Свойства логарифмов. Десятичные и натуральные логарифмы
Учебная дисциплина :Математика: Алгебра, начала математического анализа, геометрия.
Группа:1 А,1 Б,1 Д.
Тип учебного занятия: Изучение нового материала
Вид учебного занятия: Комбинированный урок
Цели учебного занятия:
Обучающая:
Формирование знаний и умений у обучающихся по теме «Десятичный и натуральный логарифм». Формирование способностей контроля и
Развивающая:
Развитие навыков по применению формул, навыков самостоятельной работы при выполнении упражнений.
Воспитательная:
воспитание у обучающихся чувства ответственности за результаты своей работы, формирование правильной самооценки, воспитание уверенности в себе, познавательного интереса к предмету
Задачи:
Повторить, обобщить и закрепить знания, полученные ранее
Отработать навыки вычисления десятичных и натуральных логарифмов
Продемонстрировать умение работать в группе.
Планируемые результаты:
Предметные:
- сформируются основы элементарных знаний по комбинаторике;
-научатся решать простейшие комбинаторные задачи практического содержания.
Метапредметные:
Регулятивные:
- научатся планировать свою деятельность в зависимости от конкретных условий;
- научатся обрабатывать информацию и ранжировать ее по указанным основаниям;
-научатся контролировать и оценивать процесс и результаты действия.
-сформируются умения проверять результаты деятельности .
Коммуникативные:
-сформируется умение устраивать эффективные групповые обсуждения и обеспечивать обмен
знаниями между членами группы для принятия эффективных совместных решений;
- научатся брать на себя инициативу в организации совместного действия.
Познавательные:
-научатся выполнять логические операции сравнения, анализа, обобщения, классификации;
-научатся выделять и формулировать познавательные цели, осознанно и произвольно строить
свои высказывания;
- научатся выбирать способы решения задач в зависимости от конкретных условий;
-научатся давать определения понятиям.
Личностные:
-умеют вести диалог на основе равноправных отношений ,взаимного уважения и принятия;
-умеют конструктивно разрешать проблемы;
- учащиеся ответственны и аккуратны;
- учащиеся уверенны в собственных силах
Технологическая карта с дидактической структурой учебного занятия
|
| Дидактическая структура учебного занятия* | Деятельность преподавателяя | Деятельность обучающихся | Задания для обучающихся, выполнение которых приведет к достижению планируемых результатов |
|
| Организационный момент | Приветствие Определение отсутствующих Входная рефлексия Организует деление на группы по 4 человека Сообщение преподавателем темы урока.
Озвучить цель урока и мотивировать деятельность обучающихся
| Приветствие Настраиваются на урок Дежурный докладывает об отсутствующих Слушают, выполняют требования преподавателя: записывают тему в тетрадь | Постановка целей и задач урока |
|
| Проверка домашнего задания | Опрос фронтальный Несколько студентов показывают решение д. упражнений Актуализировать знания ранее изученной темы для изучения новой. | Отвечают на вопросы Показывают на доске решение д.з. Устно решают примеры, применяя свойства логарифмов | Вопросы по теме «Логарифмы» |
|
| Изучение нового материала | Ввести понятие десятичного и натурального логарифмов,на их примере изучить свойства логарифмов Сообщает определения показывает на примерах, задает вопросы по решению
| Записывают определения И свойства | |
|
| Закрепление нового материала | Направляет, корректирует решение | Решают примеры из учебника Задают вопросы | №492-497 |
|
| Подведение итогов Контроль Коррекция | Подводит итоги | Выставляют себе оценки | Вопросы по изученной теме |
|
| Рефлексия | Преподаватель задает учащимся вопросы: Какая тема была изучена на занятии? Достигнута ли цель занятия? Что больше всего запомнилось на занятии?
| Отвечают на вопросы -что было сложным -что получается легче Делают выводы | Вопросы |
|
| Домашнее задание |
|
| 493-498 в,г |
| Определение. Логарифмом положительного числа b по основанию a (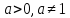 ) называется показатель степени, в которую нужно возвести основание a, чтобы получить число b. ) называется показатель степени, в которую нужно возвести основание a, чтобы получить число b. |
Например:
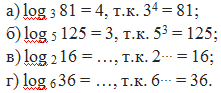
Основное логарифмическое тождество (Слайд 8)
Если корень 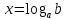 подставить в уравнение
подставить в уравнение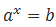 , то получим формулу
, то получим формулу 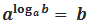 (b 0, a 0 и a 1), которая называется основным логарифмическим тождеством.
(b 0, a 0 и a 1), которая называется основным логарифмическим тождеством.
Это равенство является краткой символической записью определения логарифмов.
Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ.
Решить примеры согласно тождеству:
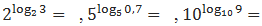
Сравните.

Основные свойства логарифмов (Слайд 9)
Основные свойства логарифмов вытекают из определения логарифма и свойств показательной функции. При любом a 0, a ≠ 1 и любых положительных x и y выполнены равенства:

Десятичные и натуральные логарифмы (Слайд 10)
На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10.
Логарифм положительного числа b по основанию 10 называют десятичным логарифмом числа b и обозначают lg b, т.е. вместо 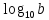 пишут lg b.
пишут lg b.
Например, 
Натуральным логарифмом (обозначается ln) называется логарифм по основанию e: 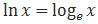
Примеры вычисления десятичных логарифмов (Слайд 11)

Задание. Вычислить 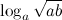 , если
, если 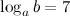
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
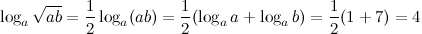
Задание. Вычислить 
Решение. Преобразуем данное выражение, используя свойство суммы логарифмов и определение натурального логарифма: