Арксинус и арккосинус числа
Тип урока: урок усвоения новых знаний.
Цели урока: ввести понятие обратной функции, её основных свойств; ввести понятия обратной тригонометрической функции арксинус и арккосинус числа, разобрать их основные свойства – область определения и множество значений, формировать навыки вычисления арксинусов и арккосинусов чисел; развивать логическое мышление, умение аргументировать.
Оборудование: мультимедийный комплекс, видеоурок, презентация к уроку.
Структура урока:
Организационный этап.
Постановка целей и задач урока. Мотивация учебной деятельности.
Актуализация опорных знаний.
Изучение нового материала.
Первичное закрепление полученных знаний.
Итог урока.
Домашнее задание.
Ход урока
I Организационный этап: Проверить готовность к уроку. Отметить отсутствующих. Настроить учащихся на учебную деятельность.
II Постановка целей и задач урока. Сообщение темы урока. Определение целей и задач урока. По мере изучения различных действий мы рассматривали и действия им обратные. К возведению в степень обратно – извлечение корня, к показательной функции обратна логарифмическая. Так и к нахождению тригонометрических функций угла существует и обратное действие – по значению синуса, косинуса найти углы, которым соответствуют эти значения. Сегодня на уроке мы узнаем как выполняются такие действия, как называются обратные тригонометрические функции и как вычисляются их значения.
III Актуализация опорных знаний.
Опрос теории: 1) какая зависимость между двумя переменными называется функцией?
2) Что такое область определения функции? Множество значений функции?
3) Когда функция монотонна на некотором интервале и какие виды монотонности вы знаете?
4) Как вводится угол в алгебре?
5) Какие значения может принимать угол)
6) Что называют синусом, косинусом числового аргумента?
7) Какое свойство называют периодичностью? Какой период имеют синус и косинус числа?
8) Обладают ли тригонометрические функции свойством четности?
Задание классу:
Из уравнения выразить 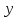 через
через 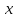 . Назвать аргумент и функцию. Выразить
. Назвать аргумент и функцию. Выразить 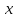 через
через 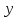 .
.
а) 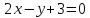 б)
б) 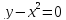 в)
в) 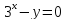
IV Изучение нового материала.
На доске записаны две зависимости 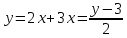 .
. 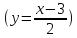 Обе функции заданы на множестве R , множество их значений тоже R. Если рассмотреть функцию
Обе функции заданы на множестве R , множество их значений тоже R. Если рассмотреть функцию 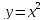 , то область её определения R, а множество значений – интервал
, то область её определения R, а множество значений – интервал 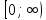 . Если рассмотреть зависимость
. Если рассмотреть зависимость 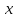 от
от 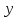 , то она не будет функцией, так как одному значению
, то она не будет функцией, так как одному значению 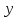 соответствует два значения
соответствует два значения 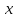 . Мы можем найти обратную функцию на подмножествах
. Мы можем найти обратную функцию на подмножествах 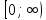 и
и 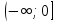 .
.
Также и тригонометрические функции имеют обратные только на определенных интервалах значений аргумента.
Рассмотрим на координатной плоскости единичную окружность с центром в начале отсчета. Проведём прямую 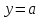 . Если число
. Если число 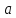 таково, что
таково, что 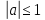 , то прямая
, то прямая 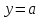 пересекает правую полуокружность в единственной точке
пересекает правую полуокружность в единственной точке 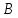 .При этом вектор
.При этом вектор 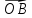 образует с вектором
образует с вектором 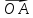 угол
угол 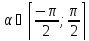 , синус которого равен
, синус которого равен 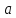 . Этот угол обозначают
. Этот угол обозначают
arcsin a = α
Определение: Арксинусом числа 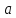 называется такой угол α, синус которого равен
называется такой угол α, синус которого равен 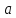 и
и 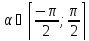 .
.
Если  , то арксинус такого числа не существует и запись arcsin a не имеет смысла.
, то арксинус такого числа не существует и запись arcsin a не имеет смысла.
Аналогично вводим понятие арккосинуса, работая с материалами учебника п. 7,6
Рассмотрим некоторые свойства арксинуса и арккосинуса
arcsin (sin  , если
, если 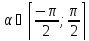 ,
,
sin(arcsin a)=a, если 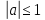
arccos(cos если
если  ,
,
cos(arccos  , если
, если 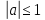 .
.
V Первичное закрепление полученных знаний.
Разобрать примеры из п 7,5 и 7,6
Решаем совместно с классом на доске № 7.77, № 7.78(а,б), № 7.79 (1,2 столб), № 7.82(а,д), № 7.86, № 7.87 (а,б), № 7.88(1,2 столб)
VI Итоги урока
Повторить основные понятия по электронной таблице
VII Домашнее задание
П 7.5, п. 7.6. определения, таблица значений № 7.78(в,г), № 7.79 (3 столб), № 7.82 (б, е), №7.87 (в, г), № 7.88(3 столб)







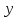 через
через 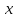 . Назвать аргумент и функцию. Выразить
. Назвать аргумент и функцию. Выразить 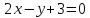 б)
б) 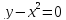 в)
в) 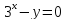
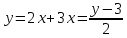 .
. 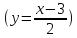 Обе функции заданы на множестве R , множество их значений тоже R. Если рассмотреть функцию
Обе функции заданы на множестве R , множество их значений тоже R. Если рассмотреть функцию 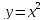 , то область её определения R, а множество значений – интервал
, то область её определения R, а множество значений – интервал 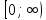 . Если рассмотреть зависимость
. Если рассмотреть зависимость 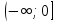 .
.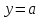 . Если число
. Если число 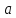 таково, что
таково, что 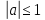 , то прямая
, то прямая 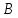 .При этом вектор
.При этом вектор 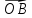 образует с вектором
образует с вектором 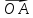 угол
угол 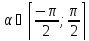 , синус которого равен
, синус которого равен 









