10 класс АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА 16.01.2024
Тема: Логарифмическая функция, её свойства и график.
Тип: изучение нового материала.
Цель: изучить логарифмическую функцию, её свойства и график.
Задачи:
Образовательные: познакомиться с логарифмической функцией, её свойствами и графиком; научиться строить график логарифмической функции.
Развивающие: развивать у учащихся технику вычисления.
Воспитательные: прививать аккуратность и правильность записи математических символов; содействовать воспитанию интереса к математике.
Автор разработки урока: Попов Дмитрий Сергеевич.
ХОД УРОКА
I.Организационный момент.
- Здравствуйте, ребята! Сегодня мы продолжаем изучать логарифмы.
Учитель проводит перекличку.
II. Проверка домашнего задания
Учитель проводит проверку и анализ выполнения домашней работы.
III. Актуализация знаний
Учитель вызывает к доске ученика, который обычно имеет оценку «3», для решения данных уравнений.
а)  ; б)
; б) 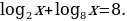
В то время, когда учащийся решает у доски уравнения, остальные ученики решают их же, но у себя в тетрадях.
IV. Постановка темы и целей урока.
- Логарифмы нашли свое применение в физике, биологии, экономике, астрономии, химии и даже в музыке. Существующая зависимость между числом и логарифмом этого числа является функцией. Как выглядит эта функция и можно ли построить ее график? Об этом мы будем говорить на сегодняшнем уроке.
- Откройте тетради, запишите дату (18.01.2024) и тему урока «Логарифмическая функция, её свойства и график».
V. Работа по теме урока. Изучение нового материала.
Учитель записывает на доске определение логарифмической функции:
Функция вида y = 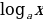 , где a – заданное число, a 0, a ≠ 1 называют логарифмической функцией.
, где a – заданное число, a 0, a ≠ 1 называют логарифмической функцией.
Свойства логарифмической функции:
1. Область определения логарифмической функции – множество всех положительных чисел.
Учитель на доске делает запись: D (у) = (0; +  ).
).
2. Множество значений логарифмической функции – множество R всех действительных чисел.
Учитель на доске делает запись: Е (у) = (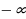 ; +
; +  ).
).
3. Логарифмическая функция неограниченна.
Учитель на доске делает запись: Логарифмическая функция неограниченна.
4. Логарифмическая функция y = 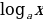 является возрастающей, если a 1, и убывающей, если 0 a Учитель на доске делает запись: возрастает, если a 1; убывает, если 0 a
является возрастающей, если a 1, и убывающей, если 0 a Учитель на доске делает запись: возрастает, если a 1; убывает, если 0 a
Если a 0 и  , где
, где  .
.
Если 0 a  , где
, где  .
.
5. Нуль логарифмической функции:
Учитель на доске делает запись: x = 1 (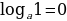 ).
).
6. Промежутки знакопостоянства (0; 1) и (1; + :
:
Учитель на доске делает запись:
Если a 0, то функция принимает положительные значения при х 1, отрицательные 0 х
Если 0 a 0 х отрицательные х 1.
- Из рассмотренных свойств логарифмической функции следует, что ее график располагается правее оси Оу, обязательно проходит через точку (1; 0) и имеет вид: если основание больше 1 (график №1) и если основание больше нуля, но меньше 1
(график №2).
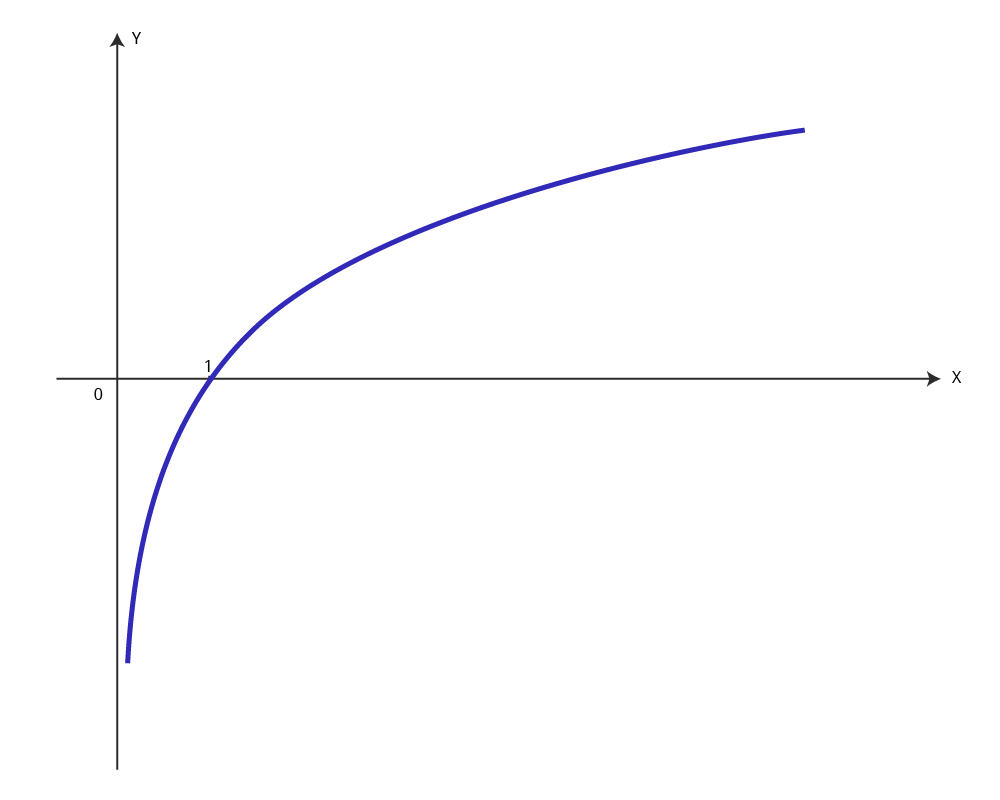
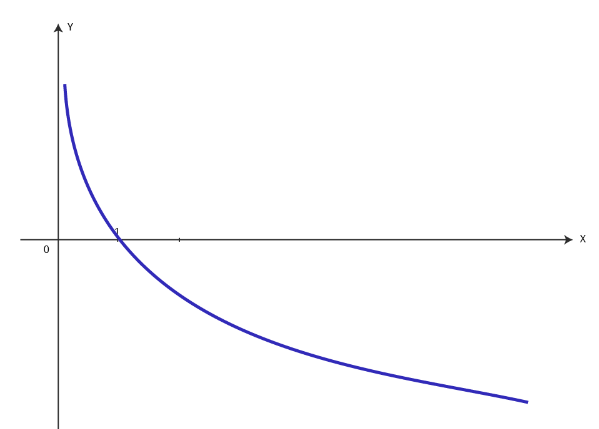
График 1 График 2
VI. Решение упражнений. Закрепление изученного материала.
1) Учитель проводит фронтальный опрос по №318, 319, 321.
2) Учитель вызывает учащихся к доске для решения №322, 324(1), 327 (1-ый столбик),
328 (1-ый столбик).
VII. Рефлексия учебной деятельности
- Продолжите предложения:
1) Сегодняшний урок заинтересовал меня …
2) Я считаю нужным запомнить …
3) Мне надо узнать лучше о …
VIII.Домашнее задание
Учитель выдаёт учащимся карточки с домашним заданием (смотреть в приложении 1).
- Вызывают ли у вас вопросы задания домашней работы? Если да, то какие?
IX. Подведение итогов урока
Оценивание рабочей деятельности учащихся на уроке.
ПРИЛОЖЕНИЕ 1







 ; б)
; б) 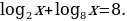
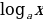 , где a – заданное число, a 0, a ≠ 1 называют логарифмической функцией.
, где a – заданное число, a 0, a ≠ 1 называют логарифмической функцией. ).
).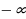 ; +
; +  , где
, где  .
. .
.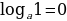 ).
). :
:

 а) возрастающая функция
а) возрастающая функция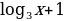 .
. …
…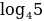 ; б)
; б) 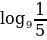 …
… ;
;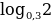 …
…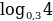 ; г)
; г) 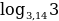 …
…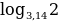 .
. ;
; 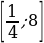 ;
; ;
; 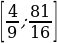 ;
;
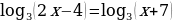 .
.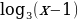 , найдите её область
, найдите её область 


















