Конспект урока по теме: "Наименьшее общее кратное"

муниципальное общеобразовательное учреждение

«Запрудненская гимназия»

Конспект урока по математике 6 класс

«Наименьшее общее кратное»

Составитель: Ерменева Ирина Викторовна

(первая квалификационная категория)

Рабочий посёлок Запрудня

2019 г.

Наименьшее общее кратное

Цели: ввести понятия наименьшего общего кратного; формировать навык нахождения наименьшего общего кратного; отрабатывать навык решения задач алгебраическим способом; повторить среднее арифметическое.

Ход урока

I. Организационный момент

 II. Работа в группах (разделить класс на группы для повторения пройденного материала и создать проблемную ситуацию для изучения нового материала)

1 группа

1. Запишите все делители чисел 20 и 30. Подчеркните все общие делители.

2. Найдите НОД (24, 36).

3. Запишите числа кратные 2.

4. Запишите числа кратные 3.

5. Подчеркните все общие кратные чисел 2 и 3.

2 группа

1. Запишите все делители чисел 22 и 33. Подчеркните все общие делители.

2. Найдите НОД (15, 35).

3. Запишите числа кратные 5.

4. Запишите числа кратные 6.

5. Подчеркните все общие кратные чисел 5 и 6.

3 группа

1. Запишите все делители чисел 30 и 40. Подчеркните все общие делители.

2. Найдите НОД (28, 42).

3. Запишите числа кратные 7.

4. Запишите числа кратные 9.

5. Подчеркните все общие кратные чисел 7 и 9.

4 группа

1. Запишите все делители чисел 18 и 24. Подчеркните все общие делители.

2. Найдите НОД (33, 44).

3. Запишите числа кратные 3.

4. Запишите числа кратные 5.

5. Подчеркните все общие кратные чисел 3 и 5.

5 группа

1. Запишите все делители чисел 36 и 9. Подчеркните все общие делители.

2. Найдите НОД (12, 35).

3. Запишите числа кратные 2.

4. Запишите числа кратные 5.

5. Подчеркните все общие кратные чисел 2 и 5.

III. Сообщение темы урока

— Сегодня на уроке мы выясним, что такое наименьшее общее кратное чисел и как его находить.

 VI. Изучение нового материала

(Задача у каждой группы на столе.)

— Прочитайте задачу.

От одной пристани к другой ходят два катера. Начинают работу одновременно в 8 ч утра. Первый катер на рейс туда и обратно тратит 2 ч, а второй — 3 ч.

Через какое наименьшее время оба катера опять окажутся на первой пристани, и сколько рейсов за это время сделает каждый катер?

Сколько раз за сутки эти катера встретятся на первой пристани, и в какое время это будет происходить?

Решение:

— Искомое время должно делиться без остатка и на 2, и на 3, то есть должно быть кратным числам 2 и 3.

— Запишем числа, кратные 2 и 3:

Числа, кратные 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.

Числа, кратные 3: 3, 6, 9, 12, 15, 18, 21, 24.

— Подчеркните общие кратные чисел 2 и 3.

— Назовите наименьшее кратное 2 и 3. (Наименьшее кратное — число 6.)

— Значит, через 6 ч после начала работы два катера одновременно окажутся на первой пристани.

— Сколько рейсов за это время сделает каждый катер? (1 – 3 рейса, 2 - 2 рейса.)

— Сколько раз за сутки эти катера встретятся на первой пристани? (4 раза.)

— В какое время это будет происходить? (В 14 ч, 20 ч, в 2 ч ночи, в 8 утра.)

Определение. Наименьшее натуральное число, которое делится на каждое изданных натуральных чисел, называется наименьшим общим кратным.

Обозначение: НОК (2; 3) = 6.

— Наименьшее общее кратное чисел можно найти и не выписывая подряд кратные чисел.

Для этого надо:

1. Разложить все числа на простые множители.

2. Написать разложение одного из чисел (лучше наибольшего).

3. Дополнить данное разложение теми множителями из разложения других чисел, которые не вошли в написанное разложение.

4. Вычислить полученное произведение.

— Найдите наименьшее общее кратное чисел:

а) 75 и 60;   б) 180, 45 и 60;   в) 12 и 35.

— Сначала надо проверить, не делится ли большее число на другие числа.

Если да, то большее число будет наименьшим общим кратным этих чисел.

— Затем определить, не являются ли данные числа взаимно простыми.

Если да, то наименьшим общим кратным будет произведение этих чисел.

а) 75 не делится на 60, и числа 75 и 60 не взаимно простые, тогда

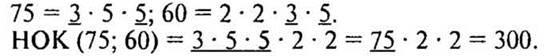
— Лучше сразу записывать не разложение числа 75, а само это число.

б) Число 180 делится и на 45, и на 60, следовательно,

НОК (180; 45; 60)= 180.

в) Эти числа взаимно простые, значит, НОК (12; 35) = 420.

 V. Физкультминутка

VI. Закрепление материала

№ 188 стр. 36 (у доски и в тетрадях).

— Прочитайте задачу.

— Что нужно сделать, чтобы ответить на вопрос задачи? (Найти НОК чисел 45 и 60.)

Решение:

45 = 3 · 3 · 5

60 = 2 · 5 · 2 · 3

НОК (45; 60) = 60 · 3 = 180, значит 180 м.

(Ответ: 180 м.)

 № 183 стр. 36 (у доски и в тетрадях).

— Найдите разложение на простые множители наименьшего общего кратного и наибольшего общего делителя чисел а и b.

а) НОК (а; в) = 3 · 5 · 7

НОД (а; в) = 5.

б) НОК (а; в) = 2 · 2 · 3 · 3 · 5 · 7

НОД (а; в) = 2 · 2 · 3.

2. № 184 (а, б) стр. 36 (с подробным комментированием).

— Расскажите, как удобнее считать.

а) НОК (а; b) = 2 · 3 · 3 · 3 · 5 · 2 · 5 = 2700.

б) Так как b делится на а, то НОК, будет само число b.

НОК (а; b) = 2 · 3 · 3 · 5 · 7 · 7 = 4410.

 VII. Повторение изученного материала

№ 200 стр. 38 (самостоятельно).

— Как по-другому можно записать частное двух чисел? (В виде дроби.)

Решение:

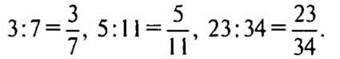
VIII. Самостоятельная работа

— Записать промежуточные ответы.

1 команда№ 227 (а—в) стр. 45,

2 команда №191 (а – в) стр. 37.

3 команда № 158(а - в) стр. 32

4 команда № 258(а-в) стр. 49

5 команда №289 (а - в) стр. 55

IX. Подведение итогов урока

— Какое число называют общим кратным данных чисел?

— Какое число называют наименьшим общим кратным данных чисел?

— Как найти наименьшее общее кратное данных чисел?

Домашнее задание

№ 207 (а, б, найти НОД и НОК), № 209 стр. 38, № 211 (а) стр. 39