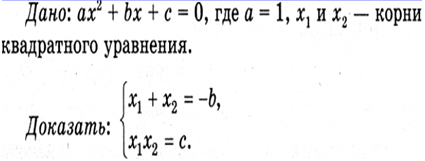Урок алгебры по теме: «Теорема Виета и её применение», 8 класс
Цели урока:
обучающая: раскрытие связей между корнями квадратного уравнения и его коэффициентами (теорема Виета); формирование способа конструирования квадратных уравнений по заданным корням (обратная теорема Виета); рассмотреть различные задания на применение теоремы Виета.
развивающая: способствовать выработке у школьников умения обобщать изучаемые факты, формулировать выводы; развивать исследовательские навыки и самостоятельность путем составления ими уравнений;
воспитывающая: научить преодолевать трудности, настраиваться на успех в любом деле; формировать навыки сотрудничества.
Тип урока: урок усвоения новых знаний.
Ход урока
І. Организационный момент
ІІ. Проверка домашнего задания
Задание на доске: решить уравнения (работают 5 учеников)
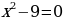
Ответ: 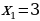 ,
, 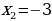
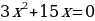
Ответ: 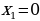 ,
, 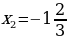
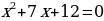
Ответ: 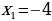 ,
, 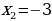
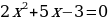
Ответ: 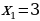 ,
, 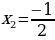
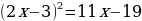
Ответ: корней нет
ІІІ. Актуализация опорных знаний
1) В это время фронтальная работа с классом:
Какое уравнение называют квадратным?
Какие виды квадратных уравнений вы знаете?
Какое квадратное уравнение называют приведенным?
Что значит решить уравнение?
Сколько корней может иметь квадратное уравнение?
Как зависит количество корней квадратного уравнения от знака дискриминанта?
2) Работа с доской
1. Укажите чему равны старший коэффициент, второй коэффициент и свободный член каждого квадратного уравнения:
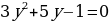 ;
;
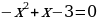 ;
;
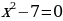 .
.
2. Преобразуйте данное квадратное уравнение в приведенное:
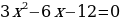 ;
;
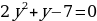 ;
;
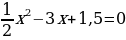 .
.
IV. Формирование знаний
Мы сегодня на уроке закрепим теоретический материал, познакомились с историческим материалом по теореме Виета, будем решать задачи на использование теоремы Виета и обратной ей теоремы.
Б иография Виеты Франсуа.
иография Виеты Франсуа.
Виета Франсуа (1540-13.12.1603), французский математик. По профессии юрист. В 1591 ввѐл буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений.
Задание для учащихся:
Группа А
Предлагается работа в тетрадях (таблица приготовлена заранее)
| Приведенные квадратные уравнения, а=1 | х 1 + х 2 | х1* х 2 |
| х2-15х+14=0 | 15 | 14 |
| х2+8х+7=0 | -8 | 7 |
| х2+9х+20=0 | -9 | 20 |
(Проверяем заполнение учащимися таблицы) Группа Б
Группа Б, составленная из более сильных учащихся, проводит исследование и на доске записывает дополнительное задание, связанное с нахождением суммы и произведения корней приведенного квадратного уравнения в общем виде.
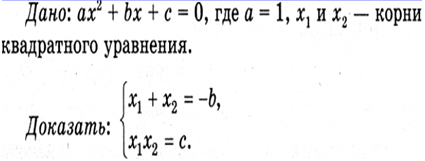

Связывание информации
– Можем ли мы сделать предположение о связи между корнями приведенного квадратного уравнения и его коэффициентами?
(х1+х2 = -р, х1•х2 =q.)
(Проведенное исследование позволяет учащимся высказать гипотезу о связи между корнями и коэффициентами приведенного квадратного уравнения.)
– Но это нужно доказать. Может быть, не для всех приведенных уравнений эти равенства справедливы?
(Ученики предполагают, что если истинность гипотезы удастся доказать путем рассуждений, то они получат новую теорему.)
Гипотеза. Если x1 и x2 – корни уравнения x2 + px + q = 0, то x1 + x2 = -р, x1· x2 = q.
Для подтверждения данной гипотезы к отчету приглашается группа Б, получившая индивидуальное задание. Ученик на доске записывает задание данной теоремы и предлагает свое доказательство этой теоремы.
– Вспомните, какая теорема называется обратной данной теореме? (Теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы, называется теоремой, обратной данной).
Формулируется теорема, обратная данной.
Если числа р, q, х1, х2 таковы, что х1 + х2 = -р, х1· х2 = q, то х1 и х2 - корни приведенного квадратного уравнения х2 + рх + q = 0.
V. Закрепление изученного материала работа с учебником
– Открываем учебник на 176 странице
Устные упражнения: №661-663.
Письменные упражнения: №665, №667, №669.
VI. Подведение итогов урока
Основные применения теоремы Виета
вычисление суммы и произведения корней квадратного уравнения, не находя при этом сами корни;
проверка правильности решения квадратного уравнения;
исследование знаков корней квадратного уравнения;
подбор корней квадратного уравнения;
составление квадратных уравнений по их корням.
VII. Домашнее задание, выставление оценок
Выучить §3 п. 19, решить №668, №670







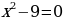
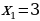 ,
, 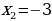
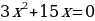
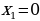 ,
, 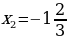
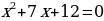
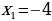 ,
, 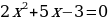
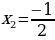
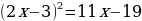
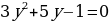 ;
;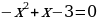 ;
;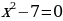 .
.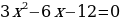 ;
;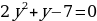 ;
;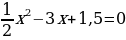 .
. иография Виеты Франсуа.
иография Виеты Франсуа.