Конспект урока по теме «Уравнение плоскости»
(Геометрия, 11 класс)
Цели:
-
ввести понятие уравнение плоскости;
-
показать, как составлять уравнение плоскости по точке и вектору нормали, по трем точкам, как находить расстояние от точки до плоскости.
Тип урока: изучение нового материала.
Методы: объяснительно-иллюстративный, репродуктивный, беседа.
План урока:
-
Организационный этап
-
Подготовительный этап
-
Объяснение нового материала
-
Закрепление нового материала
-
Подведение итогов
-
Постановка домашнего задания
Ход урока
-
Организационный этап
Учитель сообщает учащимся тему урока.
- Здравствуйте, откройте, пожалуйста, тетради и запишите тему нашего урока «Уравнение плоскости».
II. Подготовительный этап
- Сегодня мы поговорим о плоскостях. Ранее в планиметрии выводили уравнение прямой на плоскости. Кто помнит, как выглядит уравнение?
(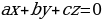 )
)
- Для чего используется это уравнение?
(Для вычисления угла между прямыми, нахождение расстояния от точки до прямой и т. д.)
- Все верно! Сейчас мы с Вами выведем аналогичное уравнение только для плоскости.
III. Объяснение нового материала
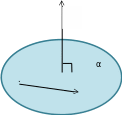
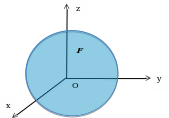 Пусть нам дана прямоугольная система координат Oxyz и дана некоторая поверхность (плоскость) F. (рис. 1)
Пусть нам дана прямоугольная система координат Oxyz и дана некоторая поверхность (плоскость) F. (рис. 1)

Рис. 1
Определение. Уравнение с тремя неизвестными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой точки, не лежащий на этой поверхности.
- Выведем теперь с Вами уравнение плоскости α, проходящей через точку 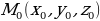 и перпендикулярной вектору нормали
и перпендикулярной вектору нормали 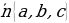 . (рис. 2)
. (рис. 2)
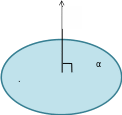

Рис. 2
- Зададим произвольную точку 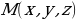 пространства, которая отлична от
пространства, которая отлична от 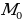 . Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы
. Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы 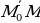 и
и 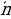 перпендикулярны. А это означает, что их скалярное произведение равно нулю. (рис. 3)
перпендикулярны. А это означает, что их скалярное произведение равно нулю. (рис. 3)
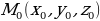
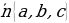
M (x, y, z)
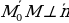
Найдем координаты 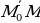 :
: 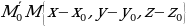
Найдем скалярное произведение 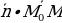 .
.
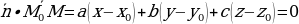
 – уравнение плоскости
– уравнение плоскости
Существует еще один способ записи уравнения плоскости. Перепишем наше уравнение плоскости.
 .
.
Домножим все на (-1) и раскроем скобки.
Получим: 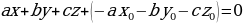 .
.
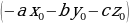 обозначим через d.
обозначим через d.
В итоге получим: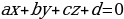 .
.
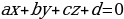 – уравнение плоскости
– уравнение плоскости
- Уравнение плоскости используется при нахождении расстояния о точки до прямой, давайте запишем с Вами формулу.
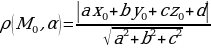 , где
, где 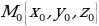 , плоскостьα задана уравнением ax+by+cz+d=0.
, плоскостьα задана уравнением ax+by+cz+d=0.
IV. Закрепление нового материала
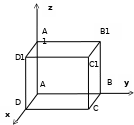

Дано:
ABCDA1B1C1D1 – куб
Составить уравнение плоскости, которая проходит через точку B и перпендикулярна вектору 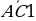 .
.
№
1
Решение:
-
Найдем координаты интересующих нас вершин: A(0, 0, 0), B(0, 1, 0), C1(1, 1, 1).
-
Найдем координаты вектора 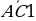 :
: 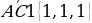 .
.
-
Подставляем координаты вектора в уравнение плоскости:
1x+1y+1z+d=0.
-
Мы знаем, что плоскость проходит через точку B(0, 1, 0). Подставляем эти координаты в найденное уравнение плоскости, чтобы найти d.
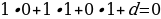
d = -1.
-
Составим уравнение плоскости: x+y+z-1=0.
Ответ: x+y+z-1=0
№2. Составить уравнение плоскости, которая проходит через точку M (-5,1, 1) и имеет вектор нормали 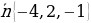 .
.
Решение:
-
-4x+2y-z+d=0
-
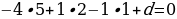
d = -21
-
-4x+2y-z-21=0.
№3. Составить уравнение плоскости, которая проходит через точку M (5, -1, 4) и имеет вектор нормали 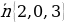 .
.
Решение:
-
2x+3z+d=0
-
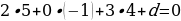
d = -22
-
2x+3z-22=0.
№4. Составить уравнение плоскости, которая проходит через точку M (4, -2, 3) и имеет вектор нормали 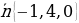 .
.
Решение:
Используем формулу  .
.
-
Подставим координаты вектора нормали:
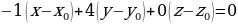
-
Подставим координаты точки:
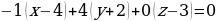
-
Раскроем скобки:
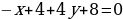
-
Составим уравнение плоскости:
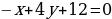 .
.
№5. Составить уравнение плоскости ABC, если известны координаты этих точек A (1, 0, 0), B (0, 1, 2), C (1, 1, 1).
Решение:
Будем искать уравнение плоскости в виде 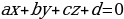 .
.
Подставим координаты точек A, B, C в уравнение:
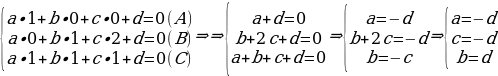
Имеем: -dx+dy-dz+d=0 (домножаем все на (-d))
x-y+z-1=0 – уравнение плоскости.
№6. Найти расстояние от точки N (10, 20, -30) до плоскости
α: 8x+6z+15=0.
Решение:
Подставляем все в формулу.
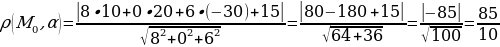
-
Подведение итогов
- Ребята, скажите, пожалуйста, с чем мы сегодня познакомились на уроке?
(Уравнение плоскости)
- Верно! Назовите мне две формулы уравнения плоскости.
( ,
, 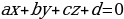 )
)
- Верно! С какой формулой мы еще сегодня познакомились?
(Формула нахождения расстояния от точки до прямой,
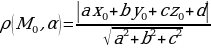 )
)
-
Постановка домашнего задания
Домашнее задание: прочесть конспект в тетради, выучить три формулы.
№1. Составить уравнение плоскости, которая проходит через точку M (-3, 1, 0) и имеет вектор нормали 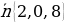 .
.
№2. Составить уравнение плоскости ABC, если известны координаты этих точек A (2, 0, 0), B (-1, 3, 0), C (2, 4, 1).






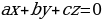 )
) Пусть нам дана прямоугольная система координат Oxyz и дана некоторая поверхность (плоскость) F. (рис. 1)
Пусть нам дана прямоугольная система координат Oxyz и дана некоторая поверхность (плоскость) F. (рис. 1)
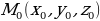 и перпендикулярной вектору нормали
и перпендикулярной вектору нормали 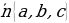 . (рис. 2)
. (рис. 2)

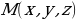 пространства, которая отлична от
пространства, которая отлична от 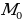 . Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы
. Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы 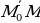 и
и 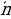 перпендикулярны. А это означает, что их скалярное произведение равно нулю. (рис. 3)
перпендикулярны. А это означает, что их скалярное произведение равно нулю. (рис. 3)
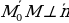
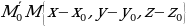
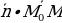 .
.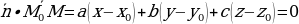
 – уравнение плоскости
– уравнение плоскости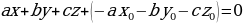 .
.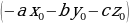 обозначим через d.
обозначим через d.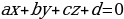 .
.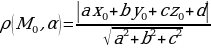 , где
, где 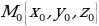 , плоскостьα задана уравнением ax+by+cz+d=0.
, плоскостьα задана уравнением ax+by+cz+d=0.

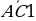 .
.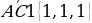 .
.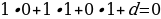
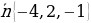 .
.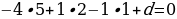
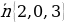 .
.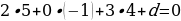
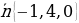 .
.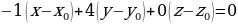
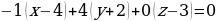
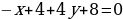
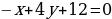 .
. 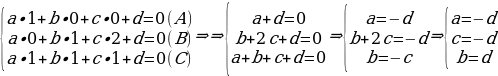
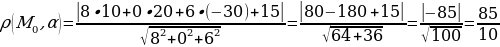
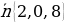 .
.

















