Тема:
Путь, перемещение и координата при равнопеременном движении
Цели урока:
1. Образовательные – познакомить с графическим способом вывода формулы для перемещения при прямолинейном равноускоренном движении, выяснить как зависит координата тела от времени при РУД, ввести понятие средней скорости при РУД, установить связь проекции перемещения и проекций начальной и конечной скорости, отработать решение задач на нахождение параметров равноускоренного движения с применением формул.
2. Развивающие – развитие таких мыслительных операций как анализ, сопоставление, сравнение, умение выделять главное, существенное в изучаемом материале. Развивать логически излагать свои мысли; развивать эмоции учащихся, создавая на уроке ситуации занимательности; формировать потребность в дополнительном, послеучебном познавательном труде; способствовать обогащению словарного запаса, прививать культуру умственного труда;
3. Воспитательные – приучать детей к аккуратному ведению записей в тетради, к доброжелательному общению, взаимопомощи, к самоконтролю; воспитывать чувство сопереживания за товарищей, формировать познавательный интерес к физике.
Тип урока: урок изучения нового материала.
Общие методы обучения: эвристический
Оборудование:
План урока
Организационный момент
Актуализация опорных знаний
Освоение нового материала
Закрепление и первичная проверка материала
Домашнее задание.
Ход урока
1. Этап начальной организации урока
Задача: подготовить учащихся к работе на уроке.
Содержание: взаимное приветствие учителя и учащихся, определить отсутствующих, проверить готовность учащихся к уроку, организовать внимание учащихся, проверить готовность оборудования.
2. Актуализация опорных знаний
Задача: вспомнить изученный ранее материал
Учитель: вспомним основные опреде ления прошлых уроков.
Фронтальный опрос:
Какое движение называется РПД?
Как найти перемещение и путь при РПД?
По какому закону изменяется скорость при РПД? Координата тела?
Что представляют собой графики зависимости Vх(t) и х(t)?
Какое движение называется РУД?
Что такое ускорение?
Поезд отходит от станции. Как направлено его ускорение?
Поезд начинает тормозить. Как направлено его ускорение?
Запишите закон изменения скорости от времени V(t) и проекции скорости Vх(t) для РУД.
Что представляют собой графики зависимости Vх(t) и х(t) при РУД?
Работа с графиками (по сборнику) - рис.56, 57 , 53
Вопросы:
Как двигалось тело на разных участках? Что общего у всех движений, чем они отличаются? На каком участке тело двигалось с большим ускорение ? На каком участке тело изменяло свою скорость менее стремительно? Если ли на графике интервал, на котором тело двигалось бы равномерно?
Вспомним
1) Как найти rх при РПД?
rх= Vхt
2) Как найти rх по графику зависимостиVх(t)?
При РПД Vх=const, площадь фигуры под графиком = rх
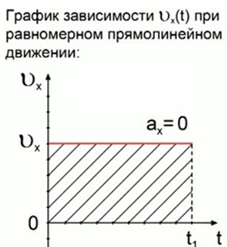
Т.о., мы знаем 2 способа, как найти rх при РПД - по формуле и графически. При РПД площадь численно будет равна модулю проекции перемещения тела.
Оказывается, этот факт можно обобщить для случая не только равномерного движения, но и для любого движения, то есть показать, что площадь под графиком численно равна модулю проекции перемещения. Это делается строго математически, но мы воспользуемся графическим способом.
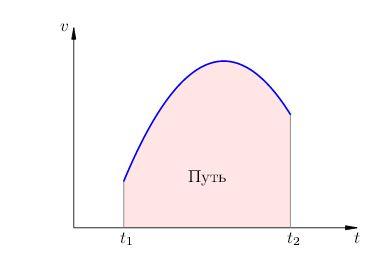
Вывод : для любого вида движения площадь под графиком скорости движения = rх .
3. Этап изучения нового материала
Задача: познакомить с графическим способом вывода формулы для перемещения при прямолинейном равноускоренном движении, выяснить как зависит координата тела от времени при РУД, ввести понятие средней скорости при РУД, установить связь проекции перемещения и проекций начальной и конечной скорости, отработать решение задач на нахождение параметров равноускоренного движения с применением формул.
 Содержание:
Содержание:
I Зависимость rх (t)
Выясним, по какому закону изменяется проекция перемещения со временем при РУД
Для этого обратимся к графику зависимости Vх(t) при РУД.

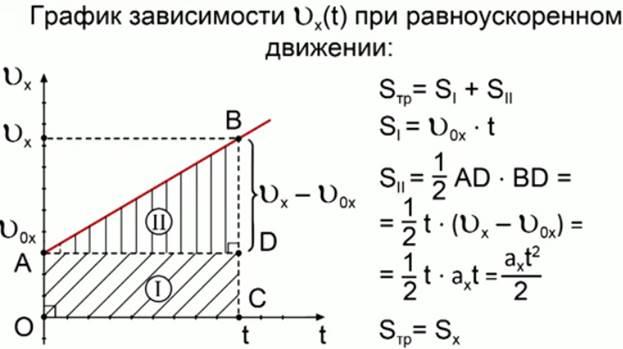
Т.к. скорость изменяется по закону Vx(t) = V0x + ахt, то при РУД график имеет вид прямой линии, она уходит вверх, если aх0 (разгон) или уходит вниз, если aх
Фигура, которую мы видим на графике, называется прямоугольной трапецией, которую можно разбить на две фигуры – прямоугольник и треугольник. Очевидно, что общая площадь будет равна сумме площадей этих фигур.
 Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, то, сложив плщади прямоугольника и треугольника, получим:
Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, то, сложив плщади прямоугольника и треугольника, получим:
rх (t) = V0xt + 
V0x- проекция начальной скорости;
ах – проекция ускорения
t – время движения (не все время, а с момента, когда было начальная скорость была = V0).



 Мы с вами получили закон зависимости проекции перемещения от времени при РУД в скалярной форме, в векторной форме он будет выглядеть так:
Мы с вами получили закон зависимости проекции перемещения от времени при РУД в скалярной форме, в векторной форме он будет выглядеть так:
 r(t) = V0t +
r(t) = V0t + 
II Зависимость x(t)
Теперь выясним, чему равна координата тела в любой момент времени, если тело движется равносукоренно.
Для любого движения х = х0 +rх,
т.к. при РУД rх(t) = V0xt +  , то
, то
х = х0 + V0xt + ахt2/2
 Мы получили решение основной задачи механики для РУД.
Мы получили решение основной задачи механики для РУД.
х = х0 + V0xt + 
Обобщение
Все до этого рассмотренные нами случаи являются частными:

Покой т.к. Vх0= 0, aх = 0, то х=х0;

РПД т.к. aх = 0, то х = х0 + V0xt

РУД х = х0 + V0xt + 
 Как же нам получить закон, по которому меняется проекция перемещения со временем при РУД?
Как же нам получить закон, по которому меняется проекция перемещения со временем при РУД?
III Средняя скорость при РУД
Вспомним
Средняя скорость перемещения находится по формуле:

 t=t
t=t
= 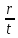 (1),
(1),


 т.к. r=
т.к. r=  t +
t +  (2)
(2)

 и V =
и V =  t +
t +  t, откуда at = V-V0 (3),
t, откуда at = V-V0 (3),


 подставив (2) и (3) в (1) (в сильных классах сам-но!) ,
подставив (2) и (3) в (1) (в сильных классах сам-но!) ,
 имеем V =
имеем V =  - средняя скорость
- средняя скорость
Вывод : средняя скорость при РУД равна среднему арифметическому начальной и конечной скорости.
В проекциях
Vх = 
Используя эту формулу, мы можем найти rx еще одним способом.
 Т.к. rх = Vxt, то rх =
Т.к. rх = Vxt, то rх = 

 Вывод : проекция перемещения – это полусумма проекций начальной и конечной скоростей, умноженная на время движения.
Вывод : проекция перемещения – это полусумма проекций начальной и конечной скоростей, умноженная на время движения.
 В векторной форме эта формула имеет вид r =
В векторной форме эта формула имеет вид r = 

IV Связь rx c Vх и V0x
Уже знаем:
(1) rх = V0xt +  – нужно знать V0х, ax, t, не нужно - Vх
– нужно знать V0х, ax, t, не нужно - Vх
(2) rх =  – нужно знать V0х, Vx, t, не нужно - aх
– нужно знать V0х, Vx, t, не нужно - aх
Получим формулу, в которой для нахождения rх не нужно будет знать t.
Вспомним, Vx= V0х + aхt, выразим из этой формулы t=  (3)
(3)
Подставим (3) в (1) (в сильных классах сам-но!)
Подставим полученное значение в первое уравнение:
Получим такое громоздкое выражение, возведем в квадрат и приведем подобные:
rх =
 =
=  или
или
 rх =
rх = 
М ы получили очень удобное выражение проекции перемещения для случая, когда нам неизвестно время движения. В этой формуле для нахождения проекции перемещения нужно знать Vx , V0х, ax, но не нужно – t.
Этих трех формул достаточно для решения задач. Выучите их наизусть!

rх = 
rх = V0xt + ахt2/2
rх = 
4. Этап закрепления и первичной проверки понимания учащимися нового учебного материала.
Задача: установить, поняли ли учащиеся новый материал. Устранить проблемы в понимании материала. Научить применять полученные знания при решении количественных задач.
Содержание:
Для того чтобы научиться пользоваться этими формулами, разберем пару типичных задач:
Задача 1 (сб. №196)
Задача 2
Автомобиль, двигаясь из состояния покоя, приобретает ускорение 2 м/с2. Найти путь, который прошел автомобиль за 3 секунды и за третью секунду. (Ответ: 9м, 5м)
Рассмотреть два способа!
3









 Содержание:
Содержание:

 Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, то, сложив плщади прямоугольника и треугольника, получим:
Учитывая тот факт, что площадь трапеции численно равна модулю проекции перемещения, то, сложив плщади прямоугольника и треугольника, получим:


 r(t) = V0t +
r(t) = V0t + 
 Мы получили решение основной задачи механики для РУД.
Мы получили решение основной задачи механики для РУД. 

 Как же нам получить закон, по которому меняется проекция перемещения со временем при РУД?
Как же нам получить закон, по которому меняется проекция перемещения со временем при РУД? t=t
t=t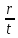 (1),
(1), 









