Конспект урока. Тема урока: Прямоугольник. Ромб. Квадрат.

Тема урока: Прямоугольник. Ромб. Квадрат.

Цель: сформировать у учащихся понятия «прямоугольник», «ромб», «квадрат» как частных случаев параллелограмма.

Задачи:

- предметные: умение проводить классификацию, логические обоснования, доказательства математических утверждений; формирование умения построения математической модели решения задач.

- метапредметные: умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки; развивать  логическое мышление, познавательную активность и навыки научной речи.

- личностные: создание педагогических условий для формирования у обучающихся положительной мотивации к учению, умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, понимать смысл поставленной задачи; выстраивать аргументацию, приводить примеры.

Тип урока: открытие новых знаний.

Основные методы обучения:  наглядный,  репродуктивный, практический и исследовательский.

Формы организации учебной деятельности:фронтальная, индивидуальная, самостоятельная, групповая.

Техническое обеспечение урока: модели четырехугольников, компьютер, карточки для исследовательской работы.

.

Ход урока.

1.Организационныйт этап.

Здравствуйте, дети! Начинаем урок. Вспомним, какую тему изучали на прошлом уроке? Что мы знаем о параллелограмме?

2. Актуализация знаний обучающихся
Можно сказать, что параллелограмм - одна из значимых фигур в планиметрии. Он обладает интересными свойствами и достоинствами. А вот какими, вы сейчас вспомните.

Ответы учащихся:

1. Противоположные стороны равны.

2. Противоположные углы равны.

3. Диагонали точкой пересечения делятся пополам.

4. Сумма углов, прилежащих к одной стороне, равна 180°.

5. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

6. Биссектрисы соседних углов параллелограмма перпендикулярны.

7. Биссектрисы противоположных углов параллельны.

8. При пересечении 4 биссектрис получается прямоугольник.

9. Каждая диагональ делит параллелограмм на два равных треугольника.

Многие из этих свойств вы сами открыли на уроке, когда изучали свойства параллелограмма. Вы на дом получили творческую работу - создать картину параллелограмма, указать одно из его свойств и доказать. Давайте проверим, что получилось. (Показываю работы учащихся, а они комментируют, что хотели выразить своим рисунком.)

3. Постановка цели и задач урока. Мотивация учебной деятельности

Класс делю на 2 группы. Каждой группе даю набор четырехугольников.

Задание: Исключите лишнюю. Почему? — Данный четырехугольник называется трапецией. Откуда такое название? 

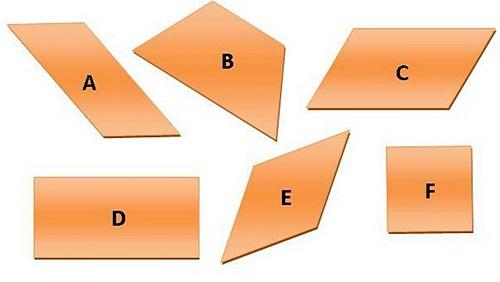
— Что общего у оставшихся фигур? Как бы вы их назвали?

Объедините параллелограммы в 2 группы. По какому признаку вы это сделали?

Первая группа - параллелограммы с неравными смежными сторонами, вторая группа – с равными сторонами, или первая группа – с прямыми углами, вторая – с острыми и тупыми.

Как называются эти параллелограммы? Какая же тема нашего урока? Что мы сегодня на уроке будем делать?

- Мы изучим определения частных видов параллелограмма и их свойства.

4. Открытие новых знаний

Сейчас вы будете «открывателями» этих свойств.

Практическая работа (исследовательского характера).

Один ученик занимается исследованием свойств прямоугольника.

Второй - занимается исследование свойств квадрата.

Третий– исследует свойства ромба.

На столах - раздаточный материал в виде изучаемых фигур, а также схема исследования. Также на столах учеников находится алгоритм действий , следуя которому учащиеся могут выполнить необходимые исследования.

Схема исследования.

Название фигуры ПРЯМОУГОЛЬНИК

Проведите исследования и закончите предложение ПРЯМОУГОЛЬНИК - это параллелограмм, у которого…

Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу:

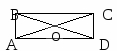
Стороны

1.  , 

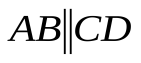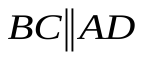
2. АВ=СD, BC=AD

Углы

1.   = 

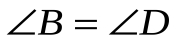
Диагонали

1. AO=OC, BO=OD.

2. АС=ВD

Схема исследования.

Название фигуры КВАДРАТ

Проведите исследования и закончите предложение КВАДРАТ - это параллелограмм, у которого…

Исследуйте стороны, углы и диагонали квадрата.

Стороны

1.  , 

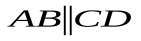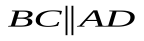
2. АВ=СD=BC=AD

Углы

1.  =

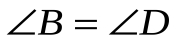
Диагонали

1. AO=OC, BO=OD

2. AC=BD

3. AC ┴ BD

Схема исследования

Название фигуры РОМБ

Проведите исследования и закончите предложение РОМБ - это параллелограмм, у которого…

Исследуйте стороны, углы и диагонали ромба.

1.  , 

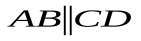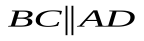
2. АВ=СD=BC=AD

Углы

1.  , 

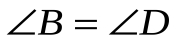
2. ,  ,

, 

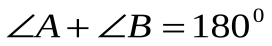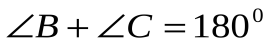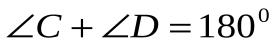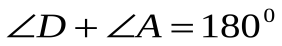
Диагонали

1. 

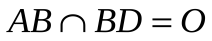
2. AO=OC, BO=OD

3. AC ┴ BD

4. AC , BD- биссектрисы углов

По окончании работы каждый ученик сообщает о результате выполненных исследований и представляет свои выводы.

4. Первичное закрепление материала

1.Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 40 ⁰

Найдите угол АОД.

Диагонали прямоугольника равны и точкой пересечения делятся пополам. 
АО=ОС=ВО=ОD ⇒
Δ АОВ - равнобедренный, и углы при основании АВ равны. 
Способ 1)
Из суммы углов треугольника найдем величину угла ВОА:
180-(40+40)=100º
Угол АОD - смежный с углом ВОА. Сумма смежных углов равна величине развернутого угла., т.е. 180º
AOD=180-100º=80º

2.найдите углы равнобокой трапеции если один из ее углов равен 30 градусов

Дано: АВСЕ — равнобедренная трапеция, угол А = 30 градусов. Найти градусные меры углов трапеции АВСЕ: угла В, угла С, угла Е — ? Решение: Рассмотрим равнобедренную трапецию АВСЕ. У нее углы при основании равны между собой, тогда угол А = углу Е = 30 градусов , угол В = углу С. Нам известно, что сумма градусных мер параллелограмма равна 360 градусам. Составляем уравнение: угол А + угол С + угол В + угол Е = 360; 30 + угол С + угол С + 30 = 360; 60 + 2 * угол С= 360; 2 * угол С = 360 - 60; 2 * угол С = 300; угол С = 300 : 2; угол С = 150 градусов. Ответ: 150 градусов; 150 градусов; 30 градусов.

3. Диагонали ромба КМНР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МНР равен 60⁰

. угол МНР = 60 по условию, значит противоположный ему угол МКР тоже будет равен 60

теперь рассмотрим угла в треугольнике КОМ

угол МОК = 90 (пересечение диагоналей ромба)

угол МКО = угол МКР : 2 = 30 (т.к диагональ ромба является биссектрисой)

угол КМО = 180 - МОК - МКО = 180 - 90 - 30 = 60

4. В равнобокой трапеции сумма углов при большем основании равна 86⁰. Найдите углы трапеции.

Углы при основаниях в равнобедренной трапеции равны
∠В=∠С
∠А=∠Д

Сумма углов по условию равна 86°.
Значит каждый угол 43°
Пусть углы при нижнем основании обозначены А и Д, оба угла острых,
∠А=∠Д=43°

Сумма углов, прилежащих к боковой стороне равна 180°.
∠А+∠В=180°, значит ∠В=180°-43°=137°
∠В=∠С=137°
О т в е т. 43°; 137°; 137°; 43°

5, .Найти стороны параллелограмма, если одна сторона больше другой в 4 раза, а периметр его 140см.

5. Рефлексия

6. Домашнее задание

Домашнее задание – творческая работа: Свои выводы после исследования свойств прямоугольника, ромба и квадрата вы оформите на отдельных листах. П.п. 45, 46.