Обобщающий урок в 7 классе
Тема урока: Уравнения. Моделирование задач.
Цель урока:
Обобщить изученный по данной теме материал.
Развивать творческую и мыслительную деятельность учащихся.
Прививать интерес к математике, к её истории.
Оборудование: Портреты Суворова, Пушкина, Пифагора, Ньютона.
Ход урока.
Организационный момент. Постановка цели.
Обобщение изученного.
а) Диктант с шифром.
| Задание | Ответ |
|
| |Х|-1=3 | -1,5 | И |
|  Х= -1 Х= -1
| -3 | А |
| (Х+3)(Х-1)=0 | 2,4 | Н |
| 5-|Х|=5 | 0 | Ф |
| 4Х+1=2Х-5 | -4,4 | Д |
| Х÷3=4÷5 | Ø | Т |
| |Х|+4=0 | -3,1 | О |
В ходе решения уравнений получается слово «Диофант»
б) Анализ уравнений, входящих в диктант. Связать с теорией.
Вопросы
Какие уравнения были в диктанте?
Что такое уравнение?
Что значит решить уравнение?
Что называется корнем уравнения?
Как называются уравнения имеющие одинаковые корни?
Какие уравнения называются линейными?
Свойства уравнений.
в) Решить уравнения:
 Ответ: Х=44.
Ответ: Х=44.
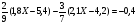 Ответ: Х=2.
Ответ: Х=2.
|Х-3|+7=1 Ответ: Ø.
5-|4+Х|=2 Ответ:-1;-7.
Из истории уравнения.
Учитель: Кто и когда придумал первое уравнение – сказать невозможно.
1 ученик: Большой вклад в развитие учения об уравнениях внёс древнегреческий математик Диофант. Он первый для обозначения неизвестных стал применять буквы. Из его работ самой важной является «Арифметика», из 13 книг которой 6 сохранились до наших дней. В сохранившихся книгах содержится 189 задач с решениями. Все задачи решаются с помощью уравнений. Недаром один неизвестный поэт сказал о нём:
«Посредством уравнений, теорем
Он уйму всяких разрешил проблем,
И засуху предсказывал и ливни
Поистине его познания дивны»
История сохранила мало сведений о жизни Диофанта. До сих пор не выяснены ни год рождения, ни дата смерти. Всё что известно о Диофанте, взято из записи на его гробнице – надписи, составленной в форме математической задачи.
Учитель: Задача о Диофанте
Путник! Здесь прах погребён Диофанта,
И числа поведать могут, о чудо, сколь долг был век его жизни.
Часть шестую его представляло счастливое детство.
Двенадцатая часть протекла ещё жизни –
Пухом покрылся тогда подбородок.
Седьмую в бездетном браке провёл Диофант.
Прошло пятилетье.
Он был осчастливлен рожденьем прекрасного первенца сына,
Коему рок половину лишь жизни счастливой и светлой
Дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец воспринял,
Пережив ещё года четыре с тех пор, как сына лишился.
Скажи, сколько лет жизни достигнув,
Смерть воспринял Диофант?

2 ученик: По- настоящему метод уравнений сформировался в руках арабских учёных.
Первым написал книгу на арабском языке о решении уравнений Мухаммед ибн
ал-Хорезми. Название у неё был очень странное – “Краткая книга об
исчислении ал-джабры и ал-мукабалы”. В этом названии впервые прозвучало
известное нам слово “алгебра”.
Что же обозначают слова «ал-джабра» и «ал-мукабала»? Ответ на этот вопрос один персидский математик изложил в следующих стихах:
3 ученик Ал-джабра
При решении уравненья
Если в части одной,
Безразлично какой,
Встретится член отрицательный,
Мы к обеим частям,
С этим членом сличив,
Равный член придадим,
Только с знаком другим, –
И найдём результат нам желательный.
Таким образом, название «ал-джабра» носила операция переноса отрицательных членов из одной части уравнения в другую, но уж с положительным знаком. По-русски это слово означает «восполнение». Поэтому с Испании, которая долгое время была под арабским владычеством, слово «алгебрист» – медицинское слово означало совсем не математика, а … костоправа. И когда Дон-Кихот был ранен в одном из поединком, его верный оруженосец Санчо Панса привёл из соседнего городка именно алгебриста.
4 ученик
Ал-макабала
Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены в нём подобны,
Сопоставить их удобно,
Вычтя равный член из них,
К одному приводим их.
А слово «ал-мукабала» означало приведение подобных членов. В отличие от слова «ал- джабра», которое в форме «алгебра» стало одним из самых употребительных в математике, про «ал-мукабалу» помнят только историки науки.
Учитель:
Задачи сводящиеся к простейшим уравнениям, люди решали на основе здравого смысла с того времени, как они стали людьми. А учебные задачи, которые мы решаем при помощи уравнений, были хорошо известны в Древнем Вавилоне, Древнем Египте, Древнем Китае, Древней Индии и Древней Греции. Давайте решим несколько таких старинных задач.
Древнегреческая задача – задача Пифагора.
– Скажи мне знаменитый Пифагор, сколько учеников посещает твою школу?
– Вот сколько – ответил Пифагор – половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и, кроме того есть ещё три женщины.
Ответ: 28 учеников.
Старинная русская задача – задача Суворова.
Эту задачу предложил решить маленькому Пушкину великий полководец А.В.Суворов, гостивший в доме Ганнибала(деда Пушкина).
Летели гуси, а навстречу гусь: «Здравствуйте 100 гусей». Ему ответили «Нас не сто. Вот если бы мы, да ещё столько, да ещё полстолька и четвёртая часть нас, вот тогда бы вместе с тобой нас было бы 100».
Ответ: 36 гусей.
Древнеегипетская задача
Пастуха, ведущего 70 быков спросили «Какую часть быков своего стада ты ведёшь?» Он ответил: «Я веду две трети от трети скота». Сколько было быков у пастуха?
Ответ: 315быков.
Старинная китайская задача
Сколько в клетке фазанов и кроликов, если всего у них 35 голов и 94 ноги.
Ответ:12 кроликов, 23 фазана.
Уравнение как математическая модель.
С помощью уравнений мы решаем не только математические задачи о числах, фигурах и т.д., но и многие прикладные задачи, условия которых содержат не математические понятия.
Решая прикладную задачу с помощью уравнения, мы как конструкторы сначала создаём математическую модель задачи (уравнение), затем решаем соответствующую математическую задачу и обязательно анализируем ответ. Решение задач на составление уравнений можно изобразить в виде схемы.
Переход от задачи к модели называется моделированием.

Самостоятельная работа.
Составить математическую модель задач (с последующей взаимопроверкой).
Частное двух чисел равно 5, а их сумма 36. Найти меньшее число.(6х+х=36)
Ответ: 6.
С начала суток прошло  того времени, которое осталось до конца суток. Который сейчас час? (
того времени, которое осталось до конца суток. Который сейчас час? (  х+х=24)
х+х=24)
Ответ: 9ч.
Отец старше сына в семь раз, а сын моложе отца на 30 лет. Сколько лет сыну?(7х-х=30)
Ответ: 5 лет.
Сумма трёх последовательных чисел равна -18. Какие эти числа? (х+х+1+х+2= -18)
Ответ: -7;-6;-5.
Чтобы сделать замазку для дерева берут известь, ржавую муку и лак в отношении 3:2:2. Сколько нужно взять каждого материала для изготовления 8,4кг замазки?(3х+2х+2х=8,4)
Ответ: 3,6 кг; 2,4 кг; 2,4 кг.
Одно число больше другого на 3. Найти эти числа, если 40% меньшего равны 70% большего. (0,4х=0,7(х+3)).
Ответ: -7; -4.
Итог урока.
Заключительное слово учителя об алгебре, как науке об уравнениях.
Ученик:
С чего начинается алгебра?
С умения всё обобщать!
Зачем выраженья похожие
Снова и снова считать?
Пускай себе числа меняются,
Мы проще поступим, хитрей,
Мы числа заменим на букву
И будем присваивать ей
Любые значения разные.
Готов в общем виде ответ!
«Пока, – говорим математике, –
Нам алгебра шлёт свой привет!»
Как символ, как знак, как начало!
Как дерзкий в решении ход!
Как путь, по которому будет
В ученьях победный исход.
Тебя ожидает удача!
Учебник бери с собой!
Пускай покорится задача!
Смелее в научный бой!
7. Домашнее задание (№ из учебника)
Подготовиться к контрольной работе






 Х= -1
Х= -1 Ответ: Х=44.
Ответ: Х=44.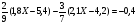 Ответ: Х=2.
Ответ: Х=2.

 того времени, которое осталось до конца суток. Который сейчас час? (
того времени, которое осталось до конца суток. Который сейчас час? ( 
















