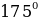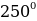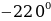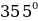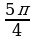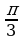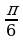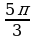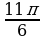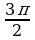МКОУ «СОШ № 10 им.А.И.Исмаилова» г.Хасавюрта РД
Урок математики в 10 «А» классе
тема урока «Определение синуса и косинуса угла»
провела: Мусаева А.И.
Январь 2021 года
Цели урока:
ввести понятия синуса и косинуса произвольного угла;
учить решать простейшие тригонометрические уравнения вида sin x = a, cos x = a при a = 0, -1, 1;
формирование интереса к математике;
воспитание культуры общения.
Планируемые результаты:
личностные:
умение анализировать над поставленной задачей, ясно и чётко излагать свои мысли в устной речи;
самоанализ результатов деятельности;
умение работать в команде, принимать общее решение.
метапредметные:
умение проводить аналогию, выделять главное, сравнивать, обобщать;
представление о математике как средстве моделирования явлений окружающего мира.
предметные:
понимание определений понятий «синус» и «косинус» произвольного угла;
умение находить значения синуса и косинуса углов, соответствующих точкам:(1;0), (0;1), (-1;0), (0; -1)
умение находить углы, синус и косинус которых равны 1, -1, 0.
УМК: Алгебра и начала математического анализа. 10-11 классы. Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.
Оборудование: учебник, презентация, карточки для работы в группах и с домашним заданием.
Ход урока
I этап. Актуализация знаний учащихся
Сегодня у нас очередной урок из раздела математики, называемого тригонометрией. Главные понятия этого раздела – это определения синуса, косинуса и тангенса угла. На следующих уроках мы будем выполнять различные преобразования тригонометрических выражений, научимся решать сложные тригонометрические уравнения.
II этап. Проверка усвоения учащимися материала предыдущего урока
I. Устно:
Найти радианную меру угла, заданного в градусах
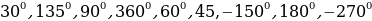
Выразить в градусной мере величину угла, заданную в радианах
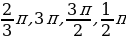
В какой четверти расположена точка, полученная поворотом точки P(1;0) на угол равный 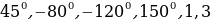 .
.
II. Найти все углы, на которые нужно повернуть точку Р (1;0), чтобы получить точку с координатами (1;0); (-1;0); (0;1) (0; -1) (работа по готовому рисунку единичной окружности).
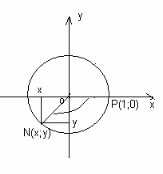
III этап. Освоение нового материала
Определение понятий «синус угла» и «косинус угла».
В 9 классе в курсе геометрии мы изучали понятия синуса, косинуса и тангенса угла 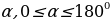 . Давайте вспомним эти определения.
. Давайте вспомним эти определения.
Предполагаемый ответ: Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе. Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.
Опираясь на эти определения и используя единичную окружность, сегодня мы выясним, что такое синус и косинус произвольного угла.
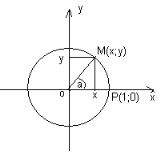
Рассмотрим единичную окружность с центром в точке О. Отметим на ней точку Р. Выполним поворот точки Р(1;0) на угол 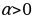 . Она займет положение точки
. Она займет положение точки 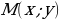 .
.
Ордината точки М называется синусом угла 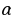 . Обозначается
. Обозначается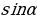 . Говорят, что
. Говорят, что 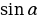 является проекцией точки М на ось
является проекцией точки М на ось 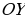 .
.
Абсцисса точки М называется косинусом угла 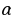 . Обозначается
. Обозначается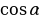 . Аналогично с синусом, говорят, что
. Аналогично с синусом, говорят, что 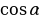 является проекцией точки М на ось
является проекцией точки М на ось 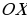 .
.
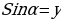 .
.
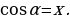
Теперь рассмотрим поворот точки Р(1;0) на угол 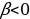 .
. 
Как вы думаете, чему равны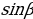 ,
, 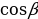 .
.
Предполагаемый ответ: 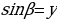 ,
, 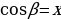
Угол может выражаться в градусах и радианах.
Задание учащимся: 1. Прочитать определения синуса и косинуса угла в учебнике.
2. Фронтальный опрос прочитанных определений.
На прошлом уроке мы работали с единичной окружностью. Давайте вспомним, какие координаты будут иметь точки, лежащие на единичной окружности.
Планируемый ответ: (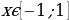 ,
, 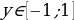 )
)
Может ли 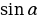 быть равным: 1) 0,035; 2)
быть равным: 1) 0,035; 2)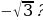
Предполагаемый ответ: 1. Может, т. к. 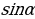 - это координата У точки единичной окружности и 0,035
- это координата У точки единичной окружности и 0,035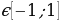 . 2. Нет, т. к.
. 2. Нет, т. к. 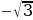 не принадлежит отрезку
не принадлежит отрезку 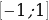 .
.
Скажите, какими могут быть значения синуса и косинуса произвольного угла?
Предполагаемый ответ: 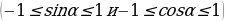 .
.
Отметим координаты точек пересечения окружности с осями координат
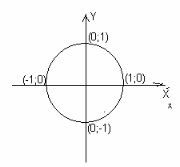 Используя этот рисунок, заполните пропуски:
Используя этот рисунок, заполните пропуски:
Задача 1.
Найти 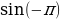 и
и 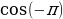
Предполагаемый ответ: (Точка М (1;0) при повороте на угол 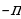 перейдёт в точку (-1;0). Следовательно,
перейдёт в точку (-1;0). Следовательно, 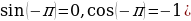
Задача 2.
Найти 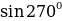 ,
,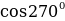
Предполагаемый ответ: Точка Р(1;0) при повороте на угол 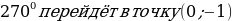 . Следовательно,
. Следовательно, 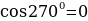 ,
, 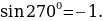
Отметить на единичной окружности точки, соответствующие числу 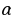 , если:
, если:
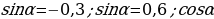 = -
= -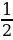
Решение простейших тригонометрических уравнений 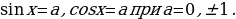
Работа в группах
Класс разбит на 3 группы
Мы ранее изучали алгебраические уравнения: линейные, квадратные; логарифмические, показательные и другие.
Уравнения вида 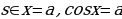 называются простейшими тригонометрическими уравнениями. Сегодня мы рассмотрим решения этих уравнений при
называются простейшими тригонометрическими уравнениями. Сегодня мы рассмотрим решения этих уравнений при 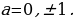
Что значит решить уравнение?
Планируемый ответ: найти значение х, при котором уравнение обращается в верное равенство или доказать, что уравнение не имеет корней.
Что значит решить тригонометрическое уравнение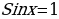 ?
?
Планируемый ответ: это значит найти все углы, синус которых равен единице, т.е. координата У=1
Как найти эти углы?
Планируемый ответ: на окружности отметить точку, ордината которой равна единице и записать углы, соответствующие этой точке.
Решить уравнение (каждая группа решает два уравнения). 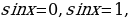
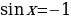 ,
,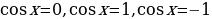
IV этап. Закрепление
Упражнение 429 учебника: отметить на единичной окружности точки, соответствующие числу α, если 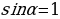 ;
; 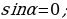
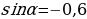 ;
; 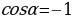 ;
; 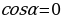 ;
; 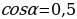 .
.
Упражнение 431: найти значение синуса и косинуса числа β, если β = 3π; 4π; 3,5π; πк; 2,5π; -5π; -0,5πк.
IV этап. Подведение итогов урока
Какие новые понятия вы узнали сегодня на уроке, чему научились?
Что показалось сложным??
Ожидаемый ответ: познакомились с определением синуса, косинуса произвольного угла. Научились находить углы, синусы и косинусы которых равны 0; 1; -1
V этап. Домашнее задание
Выучить определения синуса и косинуса угла и выполнить упражнения № 430, 432 учебника и заполнить таблицу:
Определить четверть, в которой расположена точка, полученная поворотом точки P (1;0) на угол 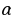
| α | 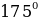
| 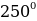
| 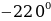
| 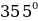
| -355 | -195 | 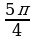
| 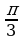
| -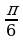 | 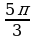
| 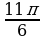
| -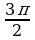 | 20π |
| Четверть |
|
|
|
|
|
|
|
|
|
|
|
|
|






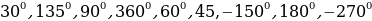
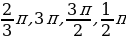
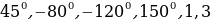 .
.
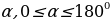 . Давайте вспомним эти определения.
. Давайте вспомним эти определения.
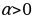 . Она займет положение точки
. Она займет положение точки 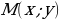 .
.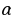 . Обозначается
. Обозначается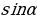 . Говорят, что
. Говорят, что 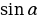 является проекцией точки М на ось
является проекцией точки М на ось 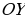 .
.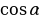 . Аналогично с синусом, говорят, что
. Аналогично с синусом, говорят, что 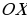 .
.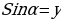 .
.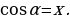
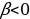 .
. 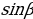 ,
, 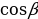 .
. 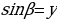 ,
, 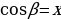
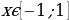 ,
, 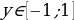 )
) 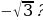
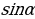 - это координата У точки единичной окружности и 0,035
- это координата У точки единичной окружности и 0,035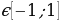 . 2. Нет, т. к.
. 2. Нет, т. к. 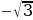 не принадлежит отрезку
не принадлежит отрезку 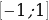 .
.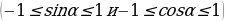 .
. Используя этот рисунок, заполните пропуски:
Используя этот рисунок, заполните пропуски: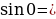
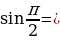
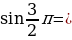
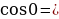
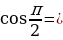
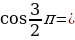
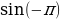 и
и 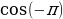
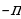 перейдёт в точку (-1;0). Следовательно,
перейдёт в точку (-1;0). Следовательно, 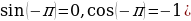
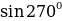 ,
,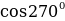
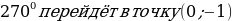 . Следовательно,
. Следовательно, 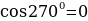 ,
, 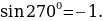
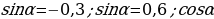 = -
= -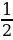
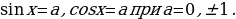
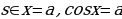 называются простейшими тригонометрическими уравнениями. Сегодня мы рассмотрим решения этих уравнений при
называются простейшими тригонометрическими уравнениями. Сегодня мы рассмотрим решения этих уравнений при 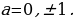
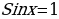 ?
?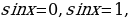
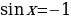 ,
,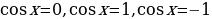
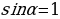 ;
; 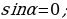
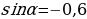 ;
; 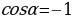 ;
; 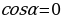 ;
; 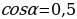 .
.