11 класс, алгебра ___________
Урок № 37
Тема: Задачи на максимум и минимум
Урок усвоения знаний и умений
Цель: обобщить и систематизировать понятия максимума и минимума функции на отрезке, точек максимума и минимума; рассмотреть алгоритм решения задач на нахождения максимума и минимума; использовать знания при решении прикладных задач.
Задачи:
1) Образовательная – использовать знания при решении прикладных задач
2) Развивающая - Развивать познавательную деятельность учащихся, творческую активность, внимание, логическое мышление, навыки самоанализа и самоконтроля;
3) Воспитательная – Воспитывать желание учиться, самостоятельность, уважение к математике.
В результате изучения темы учащиеся должны
• уметь решать прикладные задачи на нахождение наибольших или наименьших значений реальных величин;
Оборудование: учебник, презентация
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Актуализация опорных знаний
а) Фронтальный опрос:
- Что называется производной функции?
- Какие точки называются критическими?
- Как найти максимум и минимум функции?
- Как по знаку производной определить возрастает или убывает функция?
- Повторить алгоритм решения задач на нахождение максимума и минимума.
Работа с презентацией
5. Решение тренировочных упражнений
Задача 1. Число 20 запишите в виде суммы двух неотрицательных слагаемых так, чтоб сумма их квадратов была наибольшей.
Решение
Пусть первое слагаемое равняется х, тогда другое слагаемое равняется 20 – х, причём х є [0; 20].
Сумма квадратов этих слагаемых (20 – х)2 · х2. Итаке, задача сводится к нахождению такого х, при котором функция f(x) = (20 - х)2 · х2 достигает наибольшего значения на отрезке [0; 20].
Найдем производную f'(x) = 2(20 - х) · (20 - х)' х2 + (20 - х)2 · 2х = -2x2(20 - х) + + (20 - х)2 · 2х = 2х(20 - х)(20 – 2х).
С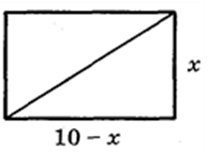 тационарными точками функции есть точки 0; 20; 10. Тогда
тационарными точками функции есть точки 0; 20; 10. Тогда
f(0) = (20 – 0)2 · 02 = 0; f(l0) = (20 - 10)2 · 102 == 10 000;
f(20) = (20 - 20)2 · 202 = 0.
Итак fнайб. = f(10) = 10 000. Таким образом, число 20 следует представить в виде 20 = 10 + 10.
Ответ: 20 = 10 + 10.
Задача 2. Среди прямоугольников, которые имеют периметр 20 см, найти тот, диагональ которого наименьшая.
Решение
Пусть длина одной из сторон прямоугольника х см, тогда другая сторона равняется (10 - х) см, де 0 х 10. Тогда(рис. 61) диагональ у прямоугольника выражается формулою у =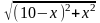 =
=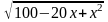 . Найдем стационарные точки:
. Найдем стационарные точки:
у' = 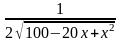 · (100 - 20х + 2х2)' =
· (100 - 20х + 2х2)' = 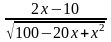 ; y’ = 0; 2x – 10 = 0;
; y’ = 0; 2x – 10 = 0;
х= 5.
Если 0 х х то у' 0, и функция возрастает. Итак, наименьшее значение функция у = 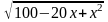 на интервале (0; 10) равняется yнайм = y(5) =
на интервале (0; 10) равняется yнайм = y(5) = 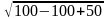 = 5
= 5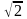 .
.
Таким образом, наименьшую диагональ 5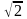 см имеет квадрат со стороною 5 см. Ответ: квадрат со стороною 5 см.
см имеет квадрат со стороною 5 см. Ответ: квадрат со стороною 5 см.
Решение упражнений (работа в парах)
1. Число 36 записать в виде произведения двух положительных чисел, сумма которых наименьшая.
Ответ: 36 = 6 · 6.
2. Забором длиной 80 м нужно оградить прямоугольный участок наибольшей площади. Найти размер участка.
Ответ: 20 х 20 м.
3. Из всех прямоугольников, площадь которых равняется 9 см2, найти прямоугольник с наименьшим периметром.
Ответ: квадрат со стороной 3 см.
(самопроверка)
6. Итог урока
-
Что, на ваш взгляд, было наиболее важным на уроке?
-
Достигнута ли цель урока?
-
Что было наиболее трудным?
8. Домашнее задание:
п. 5.9.
Задача: Как следует согнуть проволоку длиной 24 м, чтобы образовался прямоугольник наибольшей площадью?





 тационарными точками функции есть точки 0; 20; 10. Тогда
тационарными точками функции есть точки 0; 20; 10. Тогда 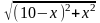 =
=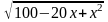 . Найдем стационарные точки:
. Найдем стационарные точки: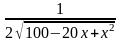 · (100 - 20х + 2х2)' =
· (100 - 20х + 2х2)' = 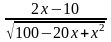 ; y’ = 0; 2x – 10 = 0;
; y’ = 0; 2x – 10 = 0;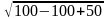 = 5
= 5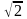 .
.



















