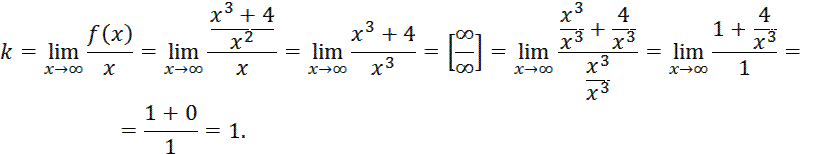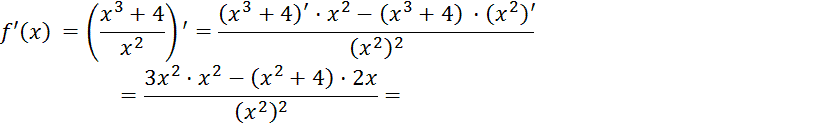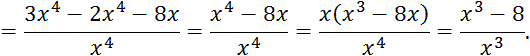Тема урока: Исследование функции с помощью производной: интервалы монотонности, экстремумы, выпуклость, вогнутость и точки перегиба.
Конспект урока
Алгоритм
Мы знаем, как по знаку производной найти интервалы монотонного возрастания или убывания функции, знаем, каким образом определить точки максимума и точки минимума функции. Пусть теперь есть задача исследовать функцию на экстремумы и на монотонность с помощью производной.
Алгоритм таков:
1. Найти  .
.
2. Выделить интервалы знакопостоянства  . Они определят интервалы монотонности
. Они определят интервалы монотонности 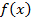 .
.
3. Найти критические точки (внутренние точки ОДЗ, в которых  или не существует).
или не существует).
4. Выделить из критических точек и концов отрезка точки экстремума и исследовать их.
Исследование функции на монотонность и экстремум
2. Исследуем функцию на монотонность и на экстремум:  Критические точки функции:
Критические точки функции:
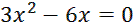 ,
,  ,
, 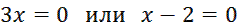


Определим знак производной в каждом интервале монотонности:
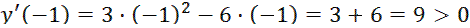
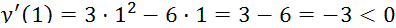
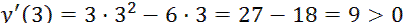
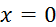 , точка max, так как производная
, точка max, так как производная  изменила знак с "+" на "−",
изменила знак с "+" на "−",
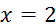 , точка min, так как производная
, точка min, так как производная  изменила знак с "−" на "+".
изменила знак с "−" на "+".
Вычислим сам экстремум функции в этих точках:
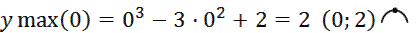

3. Исследуем функцию на выпуклость, вогнутость кривой и перегиб:

Критические точки: 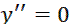 ,
,  ,
, 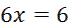 ,
, 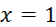
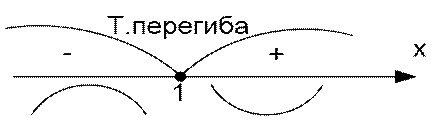
Определим знак II производной в интервале кривизны:
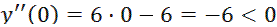 , значит, кривая выпуклая на промежутке,
, значит, кривая выпуклая на промежутке,
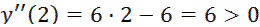 , значит, кривая вогнутая на промежутке;
, значит, кривая вогнутая на промежутке;
 Вычислим ординату точки перегиба:
Вычислим ординату точки перегиба:
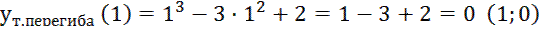
4. Найдём дополнительные точки графика:
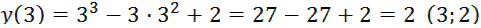
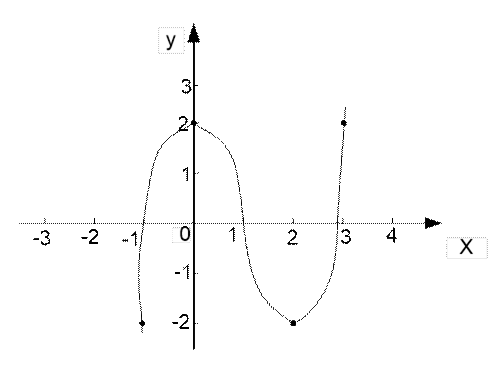
По результатам исследования строим график функции:
Пример 2. Исследовать функцию по первой и второй производной и построить её график: 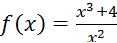 .
.
Решение: 1. Область определения функции 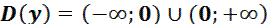 ,
,
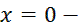 точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:
точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:

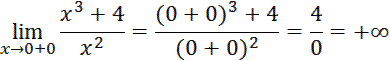 Значит,
Значит, 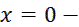 точка разрыва
точка разрыва 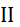 рода,прямая
рода,прямая 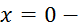 вертикальная асимптота графика функции. Найдём наклонную асимптоту графика:
вертикальная асимптота графика функции. Найдём наклонную асимптоту графика: 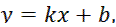 где угловой коэффициент прямой найдём по формуле
где угловой коэффициент прямой найдём по формуле
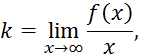
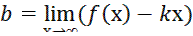
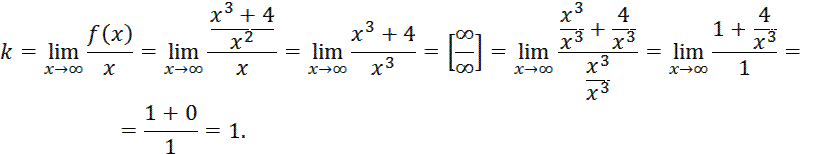
Так как  существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
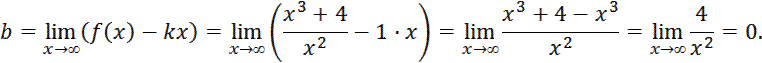
Значит, наклонная асимптота графика имеет уравнение 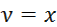 .
.
2. Исследуем функцию на монотонность и на экстремум:
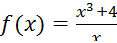 , учтем правило дифференцирования
, учтем правило дифференцирования 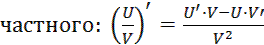
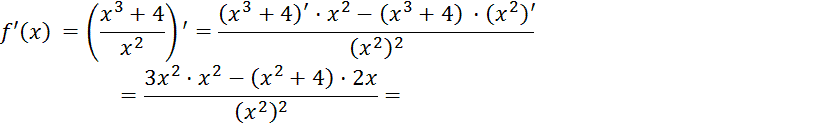
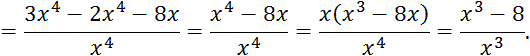
Критические точки функции:
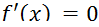 ,
, 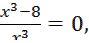
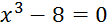 ,
, 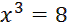 ,
,  , х=2,
, х=2,
Домашнее задание:
Определить вид функции: y=x4 -2x2 +2.
y=x4 -2x2 +2, D(y)=R.
Y=x⁴ -2x²+2
1) Область определения функции:
D(y)=(-∞; +∞)
2) Область значений функции:
Е(у)=(-∞; +∞)
3) Четность или нечетность функции:
у(-х)=(-х)⁴ - 2(-х)²+2=х⁴-2х²+2
Так как у(-х)=у(х), то функция является четной. График функции симметричен относительно оси ОУ.
4) Точки пересечения графика с осями:
ОХ: у=0
х⁴-2х²+2=0
Пусть х²=t
t²-2t+2=0
D=4-8=-4
График не пересекает ось ОХ.
ОУ: х=0
у=0⁴-2*0²+2=2
5) Промежутки возрастания и убывания функции и точки экстремума:
у' = 4x³ -4x=4x(x²-1)=4x(x-1)(x+1)
4x(x-1)(x+1)=0
x=0 x=1 x=-1
- + - +
-------- -1 --------- 0 ----------- 1 --------------
При х∈(-∞; -1]U[0; 1] функция убывает.
При х∈[-1; 0]U[1; +∞) функция возрастает.
х=-1 - точка минимума.
Уmin=(-1)⁴ - 2(-1)²+2=1-2+2=1
x=0 - точка максимума.
Уmax=0⁴-2*0²+2=2
x=1 - точка минимума.
Уmin=1⁴-2*1²+2=1-2+2=1
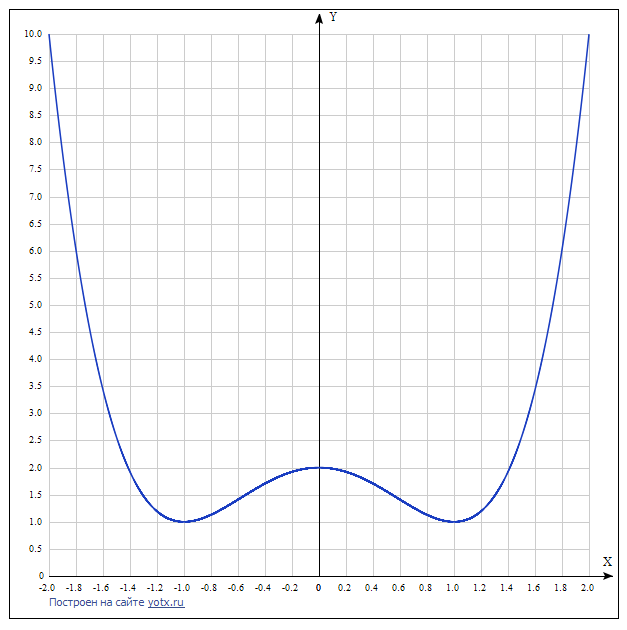
6) Точки для построения графика:
х| -2 | -1 | 0 | 1 | 2
y| 10| 1 | 2 | 1 | 10






 .
. .
. или не существует).
или не существует). Критические точки функции:
Критические точки функции: ,
,  ,
, 





 , точка max, так как производная
, точка max, так как производная  изменила знак с "+" на "−",
изменила знак с "+" на "−", , точка min, так как производная
, точка min, так как производная 


 ,
,  ,
,  ,
, 

 , значит, кривая выпуклая на промежутке,
, значит, кривая выпуклая на промежутке, , значит, кривая вогнутая на промежутке;
, значит, кривая вогнутая на промежутке; Вычислим ординату точки перегиба:
Вычислим ординату точки перегиба:



 .
. ,
, точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:
точка разрыва, чтобы определить её характер, найдём правосторонний и левосторонний пределы функции в этой точке:
 Значит,
Значит,  точка разрыва
точка разрыва  рода,прямая
рода,прямая  вертикальная асимптота графика функции. Найдём наклонную асимптоту графика:
вертикальная асимптота графика функции. Найдём наклонную асимптоту графика:  где угловой коэффициент прямой найдём по формуле
где угловой коэффициент прямой найдём по формуле


 существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
существует, то есть и наклонная асимптота. Вычисляем коэффициент b:
 .
. , учтем правило дифференцирования
, учтем правило дифференцирования 


 ,
, 
 ,
,  ,
,  , х=2,
, х=2,