Геометрия 8 класс.
Тема: "Значение синуса, косинуса и тангенса некоторых углов".
Цель: а) Закрепить применение теоремы 7.3 и значения синуса, косинуса и тангенса углов 30˚,45˚,60˚ при решении задач на вычисление;
б) Выработка и развитие у учащихся умений: самостоятельности, коллективно трудиться, самоконтроля к своим знаниям и знаниям своих товарищей;
в) Экологическое воспитание;
Ход урока.
Организационный момент. (Проверить готовность учащихся к уроку и отметить отсутствующих учащихся).
II.Проверка домашнего задания .
№54.
Дано:
ABCD – прямоугольник В С![]()
![]()
![]()
AC =2 CD
AC, BD – диагонали
Найти: ![]() AOD,
AOD, ![]() COD.
COD.![]()
Решение: I способ. А Д
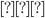 CAD – прямоугольный.
CAD – прямоугольный.
![]() CAD = 30˚, так как катет противолежащий углу 30˚, равен половине гипотенузы.
CAD = 30˚, так как катет противолежащий углу 30˚, равен половине гипотенузы.
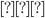 AOD – равнобедренный, так как точка пересечения диагоналей делятся пополам.
AOD – равнобедренный, так как точка пересечения диагоналей делятся пополам.
![]() OAD =
OAD = ![]() ADO=30˚, а
ADO=30˚, а ![]() AOD=120˚, так как сумма углов треугольника равна 180˚.
AOD=120˚, так как сумма углов треугольника равна 180˚.
![]() COD=180˚-120˚=60˚.
COD=180˚-120˚=60˚.
II способ.
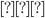 COD – равнобедренный, так как OC =
COD – равнобедренный, так как OC =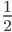 AC, то OC=OD=CD. Отсюда
AC, то OC=OD=CD. Отсюда ![]() COD=60˚,
COD=60˚,![]() AOD=120˚.
AOD=120˚.
III. Разминка.
1)Как читается теорема Пифагора?
2)Какие следствия теоремы Пифагора знаете?
3)Дайте определение косинуса острого угла в прямоугольном треугольнике.
4)Определение 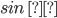 .
.
5)Определение tg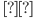 .
.
6)Какие основные тригонометрические тождества знаете?
7)Скороговорка .
8)0 1 2 3 4 5 6 7 8 9.
ч а в г л и ф я з м
Упростить выражения :
1)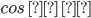 tg
tg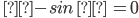 ч
ч
2)(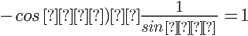 а
а
3)3+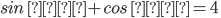 л
л
4)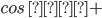 tg²α
tg²α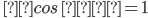 а
а
5) м
6)1 а
Какое слово получили? (ответ: чалама)
Это название местности.
Чем привлекательна эта местность ?
Раньше там много было, а теперь больше нет черёмухи, одни кусты остались.
Вы теперь наверное узнали, к чему может привести небрежное отношение к окружающей жизни. Защита природы, леса является общечеловеческой заботой, касающаяся всех. В своём докладе об экологическом воспитании подчеркивала на КМО, ШМО и так далее.
Так мы потеряли и другие прекрасные дары нашей природы. Кара-Дуруге тоже остались теперь одни кусты. А это была черёмуховая аллея. Поэтому судьба окружающей нас природы в наших руках.
Экология – наука о защите окружающей среды. Греческое слово  эко родина.
эко родина.
IV. Групповая работа.
№1 – первая группа.
1)Доказать, что для любого острого угла α,
.
2)Диагональ ромба равна его стороне и равна 10 см, вычислите вторую диагональ и углы ромба.
3)Диагональ параллелограмма равна α и перпендикулярна его стороне. Чему равны стороны параллелограмма, если его угол равен 30˚.
№2.
1)Как найти значения синуса, косинуса и тангенса углов 45˚.
2)Радиус окружности, описанной около квадрата, равен 4 см. Определите сторону квадрата.
3)Диагональ параллелограмма равна α и перпендикулярна его стороне. Чему равна сторона параллелограмма, если его угол равен 45˚.
№3.
1)Как найти значения синуса, косинуса, тангенса углов 30˚.
2)Углы при основании трапеции равны 45˚ и 30˚, а высота трапеции равна 6 см. Найдите боковые стороны трапеции.
3)Диагональ параллелограмма равна α и перпендикулярна его стороне. Чему равны стороны параллелограмма, если его угол равен 60˚.
№4.
1)Как найти значения синуса, косинуса и тангенса углов 60˚.
2)Сторона ромба равна α, а один из его углов равен 120˚.Чему равны диагонали ромба?
3)Найдите  и tgα, если
и tgα, если  =
=  .
.
№5.
1)Доказать, что для любого острого угла α ,
2)Диагональ ромба равна его стороне и равна 8 см, вычислите вторую диагональ и углы ромба.
3)Найдите 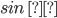 и tgα, если
и tgα, если
 .
.
№6.
1)Как найти значения синуса, косинуса и тангенса углов 45˚.
2)Радиус окружности, описанной около квадрата, равен 2 см. Определите сторону квадрата.
3)Найдите  и tgα, если
и tgα, если
№7.
1)Как найти диагонали синуса, косинуса и тангенса углов 30˚.
2)Углы при основании трапеции равны 60˚ и 30˚, а высота трапеции равна 3 см. Найдите боковые стороны трапеции.
3)Найдите  и tgα, если .
и tgα, если .
V. Дома №48/21.
VI.Итоги урока.
















