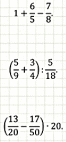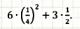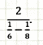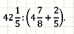Конспект занятия предметного курса по математике в 5 классе по теме "Происхождение дробей"

Предметный курс по математике «За страницами учебника математики».

Класс: 5В.

Тема: Происхождение дробей.

Цели:

1) способствовать формированию знаний о происхождении обыкновенных дробей, применении их в разных отраслях человеческой деятельности; закреплению умения выполнять все действия с обыкновенными дробями, различать правильные и неправильные дроби;

2) развивать внимание, память, логическое мышление, вычислительные навыки;

3) воспитывать интерес к предмету математики, через использование исторического материала и разных форм работы на занятии; терпимость к одноклассникам.

Ход занятия:

1. Организационный момент. Приветствие присутствующих.

Прозвенел звонок, а это значит, что наше занятие началось. Я приветствую всех присутствующих сегодня на уроке. Я рада, что вы пришли на урок, чтобы узнать что-то новое из этой сложной, но очень интересной и занимательной науки.

2. Постановка цели урока.

Мотивация учебной деятельности учащихся.

Сценка.

Ученик в одежде повара. Готовит тесто для пряников.

- Для пряников понадобится 1 яйцо, один с четвертью стакана муки, две с половиною столовой ложки меда, треть чайной ложки соли, половина чайной ложки имбиря. Всё тщательно перемешиваем и печем пряники.

Тема нашего сегодняшнего занятия…? (действительно связана с дробями). Сегодня мы поговорим о происхождении дробей.

Какую цель вы можете себе поставить?

Эпиграф к нашему занятию звучит так: «Без знания дробей никто не может признаваться знающим арифметику!» Это высказывание римского оратора и писателя Цицерона.

Согласны ли вы с ним и почему?

3. Изучение нового материала.

Есть люди, которые считают, будто дробям нет места в нашей жизни. Они думают: «Зачем математики придумали дроби? Наверное, только для того, чтобы портить жизнь школьникам». 

На самом деле в обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа.

А знаете ли вы, как и когда появились дроби?

История возникновения дробей

Память человечества не сохранила для нас имя изобретателя колеса. Также невозможно назвать точно даже тот отрезок времени, когда появились дроби.

Можно предположить, что потребность делить целое на части возникала ещё в первобытном обществе. Могло быть и так…

Были у древнего человека жена и двое детей. Вот пошла однажды древняя женщина собирать плоды и нашла всего лишь 1 яблоко. Детей у неё двое, а яблоко одно. Наверное, она догадалась: взяла каменный нож да и разделила это яблоко на 2 половины.

А в это время самый - самый древний человек пошёл на охоту и убил самого - самого древнего кабана. Пришёл домой и разделил свою добычу на четыре равные части: себе, жене, сыну и дочке. Конечно, эти древние люди и не догадывались, что, разделив целое число на части, они занимались таким трудным разделом математики, который впоследствии назовут «Дроби».

Итак, дроби появились в тот период времени, когда в трудовой деятельности людей появилась потребность более точно измерять какие-то величины, хотя делением на части люди пользовались, наверное, с древнейших времён.

Выступление учащихся с мини сообщениями:

1) Дроби в Древнем Египте (1 ученик).

В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.

Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.

В Древнем Египте некоторые дроби имели свои особые названия – а именно, часто возникающие на практике 1/2, 1/3, 2/3, 1/4, 3/4, 1/6 и 1/8. Кроме того, египтяне умели оперировать с так называемыми аликвотными дробями (от лат. - несколько) типа 1/n – их поэтому иногда также называют «египетскими»; эти дроби имели свое написание: вытянутый горизонтальный овальчик и под ним обозначение знаменателя. Одним из первых известных упоминаний о египетских дробях является математический папирус Ринда.

У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби (большие чем 1/2).

Остальные дроби они записывали в виде суммы долей. Дробь 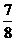  они записывали в виде  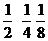,но знак «+» не указывали. А сумму  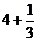 записывали в виде  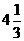. Следовательно, такая запись смешанных чисел (без знака «+») сохранилась с тех пор.

2) Дроби в Древнем Риме (2 ученик).

Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью - весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.

Даже сейчас иногда говорят: "Он скрупулёзно изучил этот вопрос." Это значит, что вопрос изучен до конца, что не одной самой малой неясности не осталось. А происходит странное слово "скрупулёзно" от римского названия 1/288 асса - "скрупулус". В ходу были и такие названия: "семис"- половина асса, "секстанс"- шестая его доля, "семиунция"- половина унции, т. е. 1/24 асса и т. д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, т. е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.

3) Дроби на Руси (3 ученик).

В русском языке слово "дробь" появилось лишь в VIII веке. Происходит слово "дробь" от слова "дробить, разбивать, ломать на части". У других народов название дроби также связано с глаголами "ломать", "разбивать", "раздроблять".

Старейшим арифметическим памятником Киевской Руси является сочинение о календаре, написанное на славянском языке в 1136году и названное «Учение им же ведати человеку числа всех лет», то есть «Наставление, как человеку познать счисление лет». автор сочинений – учёный монах Кирик Новгородец, о жизни которого известно немного. Кирик пользуется конкретными дробями: 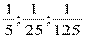 и т. д.

В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находили следующие названия дробей на Руси:

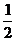– половина, полтина,  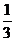– треть,

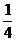– четь,  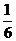– полтреть,

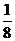– полчеть,  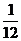– полполтреть,

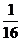– полполчеть,  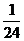– полполполтреть (малая треть),

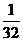– полполполчеть (малая четь),  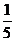– пятина,

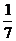– седьмина,  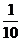– десятина.

Древние математики 100/11 не считали дробью. Остаток от деления 1 фунт предлагается поменять на яйца, которых можно было купить 91 штуки. Если 91:11 то получится по 8 яиц и 3 яйца в остатке. Автор рекомендует отдать их тому, кто делил, или же поменять на соль, чтобы посолить яйца.

Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.

Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.

А сейчас я предлагаю вам решить задачу (работа в группах по 4 человека) из «Папируса Ахмеса» (Египет, 1850 г до н.э.):

«Приходит пастух с 70 быками. Его спрашивают:

- Сколько приводишь ты своего многочисленного стада?

Пастух отвечает:

- Я привожу две трети от трети скота. Сочти!»

Решение:

1) 70:2·3=105 голов - это 1/3 от скота

2) 105·3=315 голов скота – всего

Ответ: 315 голов скота.

Физминутка. Игра «Верю-не верю (хлопок в ладоши, топот ногами). Тема «Правильные и неправильные дроби»:

7/8, 45/43, 1/2, 5/9, 6/6, 100/1000, 12/12.

Живя в окружении дробей, мы не всегда их явно замечаем. И все же, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее.

Предлагаю вам поработать с текстом (раздаточный материал) и привести примеры в каких отраслях встречаются дроби.

В медицине. Чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или, когда врач назначает больному ½ таблетки.

Дроби в кулинарии. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.

Дроби в музыке. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.

Дроби в спорте. Когда смотрим ½ финала матча по футболу.

Дроби в пропорции человека тоже связаны с дробями. Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».

Дроби в юридической деятельности. Взрослые в жизни встречаются с такими ситуациями: в наследство каждый по завещанию получили, например А- 1/8 имущества наследодателя; Б. – 6/17; В. - завещано всё остальное . Какие доли достались каждому из наследников?

Дроби для портных. Портной при раскрое одежды использует дроби. (рукав длины три четверти -  ¾ или брюки длины 7/8)

Это лишь малая часть того, где мы можем увидеть присутствие дробей.

4. Решение заданий из ОГЭ.

В настоящее время невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел.

Поэтому и по завершении вами 9 класса на экзамене по математике, который вы будите сдавать все без исключения, есть задания с дробями. Мы с вами, обучаясь в 5 классе, уже можем решить № 6 из ОГЭ по математике. Что я и предлагаю вам сейчас сделать.

Решение заданий № 6 ОГЭ (работа в парах, разные задания по уровню сложности, по желанию учащихся):

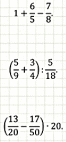
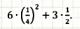
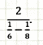
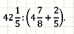
Проверка по слайду.

5. Подведение итогов занятия.

Без знания математики, особенно знания дробей вся современная жизнь была бы невозможна. Например, у нас не было бы хороших домов, потому что строители должны уметь измерять, считать, сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, то есть точно все измерить. Не было бы ни какой большой промышленности, ни какой коммерции.

И конечно, не было бы радио, телевидения, кино, телефона и тысяч других вещей, составляющих часть нашей цивилизации. Использование дробей является жизненно необходимой частью мира, в котором мы живем.

Добились ли вы той цели, которую ставили перед собой в начале занятия?

Что для вас было трудным, непонятным?

Что понравилось, запомнилось?

6. Рефлексия.

На экране модель солнца, у каждого на партах есть лучики, оцените своё настроение и лучик соответствующего цвета мысленно прикрепите к солнышку (покажите их):

на уроке было интересно, и вы достигли поставленной цели (розовый)

на уроке было интересно, но вы не достигли поставленной цели (жёлтый)

на уроке было не интересно (зеленый)

7. Домашнее задание. (на выбор)

1) найти старинные задачи с обыкновенными дробями;

2) приготовить доклад «Применение дробей в конкретной профессии»;

3) приготовить мини сообщение «Появление дробей» (в древних странах и цивилизациях, о которых сегодня не говорилось).

Наше занятие хочу закончить словами Л.Н. Толстого:

«Человек подобен дроби, числитель есть то, что он есть,

а знаменатель то, что он о себе думает.

Чем больше знаменатель, тем меньше дробь».

Всем спасибо за работу.