Урок геометрии в 7 классе
Тема: «Параллельность прямых»
Предметные цели урока: организовать деятельность учащихся по изучению и первичному закреплению аксиомы параллельных прямых и ее следствий, понятий об аксиомах геометрии.
Ход урока
Организационный момент
Приветствие, проверка готовности к уроку. Сообщить тему урока, сформулировать цели на урок.
Проверка выполнения домашнего задания
Двое учащихся решают задачи по готовому чертежу
А



![]()
 а) 1 2 б) B
а) 1 2 б) B
 C
C

![]() ┌ D C D
┌ D C D
 Е
Е
| Дано: ∆АВС, BD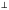 AC; AC; АС – биссектриса BAE Доказать: ВС | | АЕ Доказательство. 1. ∆АВD = ∆CВD по II признаку 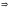 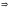 BAD = BCD. BAD = BCD.
2. АС – биссектриса BAE 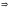 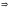 BAD = DAE, а они накрест лежащие при прямых ВС и АЕ и секущей АС BAD = DAE, а они накрест лежащие при прямых ВС и АЕ и секущей АС 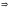 ВС | | АЕ ВС | | АЕ
| Дано: ∆АВС, АС – биссектриса BAD; ВЕ 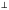 АС; АЕ = ЕС АС; АЕ = ЕС Доказать: AD | | BC Доказательство. 1. ∆АВЕ = ∆CВЕ по I признаку 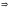 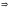 BAЕ = BCЕ. BAЕ = BCЕ.
2. АС – биссектриса BAD 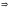 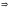 BAE = DAE, а они накрест лежащие при прямых ВС и АD и секущей АС BAE = DAE, а они накрест лежащие при прямых ВС и АD и секущей АС 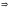 ВС | | АD ВС | | АD
|
Класс работает устно по готовому чертежу (слайд)

 2
2
![]() а 120º c d
а 120º c d
1 20º Используя данные рисунка найдите углы
![]() b 2 160º
b 2 160º
Подготовка учащихся к активной учебно-познавательной деятельности на основном этапе занятия
Фронтальный опрос.
Закончи предложение. (слайд)
1. Прямая х называется секущей по отношению к прямым а и b, если…
2. При пересечении двух прямых секущей образуется … неразвернутых углов.
3. Если прямые АВ и СD пересечены прямой ВD, то прямая ВD называется…
 4. Если точки В и Dлежат в разных полуплоскостях относительно секущей АС, то углы ВАС и DCA называются…
4. Если точки В и Dлежат в разных полуплоскостях относительно секущей АС, то углы ВАС и DCA называются…
![]() А В
А В
 D C
D C
 5. Если точки В и D лежат в одной полуплоскости относительно секущей АС, то углы ВАС и DCA называются…
5. Если точки В и D лежат в одной полуплоскости относительно секущей АС, то углы ВАС и DCA называются…
![]() В А |
В А |
 D
D
C
6. Если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары…
Найди соответствие (слайд)
|  А) m А) m
![]() a 50° a 50°
![]() b 130° b 130°
|
1) a | | b, так как внутренние накрест лежащие углы равны
|
|   Б) a b Б) a b
![]() m 45° 45° m 45° 45°
| 2) a | | b, так как соответственные углы равны
|
|   В) а В) а
150°  150° b 150° b
m |
3) a | | b, так как сумма внутренних односторонних углов равна 180°
|
Изучение новых знаний и способов действий
Беседа об аксиомах геометрии (слайды)
Понятие следствия и рассмотрение следствий аксиомы параллельных прямых (слайды)
Первичная проверка понимания изученного
Тест на два варианта.
Отметить знаком «+» правильные утверждения и знаком «-» - ошибочные.
Вариант 1
1. Аксиомой называется математическое утверждение о свойствах фигур.
2. Аксиомой называется математическое утверждение о свойствах геометрических фигур, требующее доказательства.
3. Через любые две точки проходит прямая.
4. На любом луче от начала можно отложить отрезок, равный данному, и притом только один.
5. На любом луче от начала можно отложить отрезки, равные данному, причем сколько угодно много.
6. От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.
7. Через точку не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
8. Через точку, не лежащую на данной прямой, проходит множество прямых, параллельных данной.
9. Если две прямые параллельны третьей, то они параллельны между собой.
10. Если прямая пересекает одну из двух параллельных прямых, то она параллельна другой прямой.
Вариант 2
1. Аксиомой называется математическое утверждение о свойствах геометрических фигур, принимаемое без доказательства.
2. Аксиомы используются при доказательстве теорем.
3. Через любые две точки проходит прямая, и притом только одна.
4. На любом луче от его начала можно отложить два отрезка, равных данному.
5. От любого луча в заданную сторону можно отложить угол, равный данному.
6. От любого луча в заданную сторону можно отложить угол, равный данному, и притом только один.
7. Через точку, не лежащую на данной прямой, проходят только две прямые, параллельные данной.
8. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
9. Если прямая пересекает одну из двух параллельных прямых, то она перпендикулярна другой прямой.
10. Если две прямые параллельны третьей, то они перпендикулярны между собой.
Закрепление знаний и способов действий учащихся (задания из учебника)
Информация о домашнем задании
Подведение итогов учебного занятия
Рефлексия деятельности
Учитель предлагает закончить предложения:
«Сегодня на уроке я понял(а), что мне необходимо…»
«При решении показательных неравенств необходимо…»
«Самое трудное для меня…»










 C
C
 Е
Е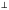 AC;
AC;

 2
2 









