Конспект урока "Параллелограмм. Свойство диагоналей параллелограмма.

Тема. Параллелограмм. Свойство диагоналей параллелограмма.

Цель: ввести определение, понятие о признаках и свойствах параллелограмма; научить доказывать соответствующие теоремы и применять их при решении задач; содействовать рациональной организации труда обучающихся.

Ход урока

1. Оргмомент.

2. Актуализация опорных знаний.

1. Устно по рисунку определить: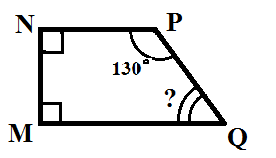

а) Параллельны ли прямые NP и MQ? (Да)

б) Параллельны ли прямые MN и PQ? (Нет)

в) Чему равен угол Q?

2. Задача. В четырехугольнике ABCD все стороны равны. Докажите, что противолежащие углы A и C равны. (Сделайте дополнительное построение: проведите диагональ BD).

3. Какая фигура называется четырехугольником?

III. Сообщение темы урока.

– Сегодня на уроке мы начнём знакомиться с видами четырёхугольников. Первый из них параллелограмм . Введём определение параллелограмма, а так же понятие о признаках и свойствах параллелограмма.

1. Формирование новых понятий.

1. Стр. 68, пункт 51. - прочитайте определение параллелограмма, подготовьтесь отвечать на вопросы.

– Какую фигуру можно назвать параллелограммом? ( Четырёхугольник)

– Какая отличительная особенность у параллелограмма от других четырёхугольников?

Построим чертёж.

Задание запишите пары параллельных сторон.

Выводы :

1.Противолежащие стороны параллелограмма попарно параллельны.

2.Если противолежащие стороны попарно параллельны, то четырёхугольник является параллелограммом.

2) Теорема .

Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Дано: ABCD четырёхугольник, AC BD = O; AO = OC, DO = OB.

Доказать : ABCD параллелограмм.

Доказательство:

– Что нам нужно доказать?

– Что мы знаем по определению параллелограмма?

– Как можно доказать, что AB || DC ? ( если внутренние накрестлежащие углы при секущей DB равны)

– Как можно доказать, что углы равны? ( Через равенство треугольников)

– Какие треугольники рассмотрим?

Запишите доказательства в тетрадь.

ABC = COD (по двум сторонам (по условию) и углу между ними ( вертикальные)).

Из равенства треугольников следует угол BDC равен углу DBC (соответствующие), следовательно AB || DC.

Аналогично доказываем AD || BC.

Т.к. противолежащие стороны попарно параллельны, то ABCD – параллелограмм (по определению). .

V. Физминутка.

VI. Рассмотрим свойство диагоналей параллелограмма.

1. Стр. 69 пункт 52.

Теорема. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

– Что можно назвать условием данной теоремы?

–Что будет заключением в этой теореме?

– Какой является это теорема по отношению к предыдущей?

– Прочитайте доказательство теоремы в учебнике и перечертите в тетрадь чертёж рис. 120 и запишем краткое доказательство.

Дано: ABCD параллелограмм, AC и BD его диагонали.

Доказать: AO = OC; BO = OD.

Доказательство:

1. Построения: точка О (ВО = ОD), отрезок AC₁ (AO = OC₁).

2. ABC₁D – параллелограмм (по определению)

3. ABCD совпадает с ABC₁D.

Вывод : ABCD - параллелограмм (AO = OC; BO = OD).

1. Закрепление теоремы.

Задача 1. ABCD параллелограмм . О – точка пересечения диагоналей.

1. Диагональ АС = 12 см. Чему равен отрезок ОА?

2. Отрезок BO = 3 см. Чему равна диагональ BD?

3. Докажите, что OD является медианой треугольника ACD.

Задача 2. Сторона AB параллелограмма ABCD равна 7 см, диагонали AB и CD равны 6 и 10 см соответственно. О – точка пересечения диагоналей. Определите периметр треугольника AОB. (15см)

VII. Решение задач.

№6 – (разобрать по учебнику стр. 69)

№7 Дано : ABCD – параллелограмм ВЕ = 2 метра, АF = 2.8 метра.

Найти: ВС – ? АD – ?

Решение. ОЕ = ОF (смотри решение задачи №6).

BEO = DFO ( ). Следовательно FD = BE; AD = 2.8 +2 = 4.8(см).

Аналогично EOC = FOA. Следовательно EC = AF; BC = 4.8 см.

Ответ: AD = BC = 4.8см.

VIII. Итог урока.

• Что такое параллелограмм?

• Сформулируйте свойства диагоналей параллелограмма.

IX. Домашнее задание. п. 51, 52 – читать, теоремы, доказательства – учить. Вопросы 6, 7, 8. Задачи № 9, 20.