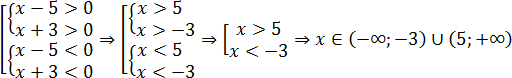Урок № 80 Конспект урока по алгебре 8 класс
тема «Метод интервалов»
Цели урока:
Образовательная: обеспечение усвоения решения квадратных неравенств методом интервалов.
Развивающая: развитие умений анализировать, выделять главное,
обобщать.
Воспитательная: формирование у учащихся навыков самостоятельной работы, воспитание внимания, сообразительности и аккуратности.
Ход урока:
Оргмомент
Устная работа а)Какие неравенства соответствуют промежуткам
[0+∞) (-∞ 5) [-3 5) (-∞ -5]
б) Какие неравенства соответствуют геометрическим моделям:



в) Какие промежутки соответствуют геометрическим моделям:




г) Разложить многочлен на множители:
х2-4=
х3-х=
д) Решите неравенства: 1) х2 - 9 ≤ 0 2) х2-5х+6≥0
3) (х-3)(х+4)(2х-5)0
3. Постановка проблемы.
На предыдущих уроках мы научились решать квадратные неравенства. Для чего же нам нужен еще и метод интервалов? Допустим, нам надо решить вот такое неравенство: (x − 5)(x + 3) 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Т.е. неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
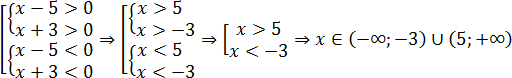
Второй вариант – раскрыть скобки, в результате получается квадратное неравенство, графический метод решения которого также хорошо отработан.
Имеем: x2 − 2x − 15 0. Ветви параболы направлены вверх, т.к. коэффициент a = 1 0. График пересекает ось OX в точках x = 5 и x = −3.
Эскиз этой параболы:
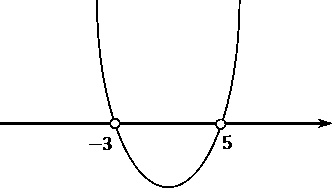
Функция больше нуля там, где она проходит выше оси OX, т.е. интервалы (−∞ −3) и (5; +∞)
Почему эти методы неэффективны? Мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
И это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4.
Например: (x − 7)(x − 1)(x + 4)(x + 9)
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости. Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
4. Изучение нового материала.
Что такое метод интервалов?
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) 0 и f (x)
Решить уравнение f (x) = 0;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имеет вид f (x) 0, или знаком «−», если неравенство имеет вид f (x)
5. Закрепление
1. Разобрать решение неравенств:
а) (x − 2)(x + 7)
б) x 3 − х
в) (х 2 – 9)(х + 3)(х - 2) 0. На решение этого неравенства обратить особое
внимание, т.к. при переходе через х = – 3 знак на соседних интервалах не меняется.
2. Работа в парах.
Каждой паре учеников предлагается решить неравенства и заполнить таблицу 1 (решению каждого неравенства соответствует буква, ее и нужно занести в таблицу)
| 1 | (2 – х)(8 – х) |
| х ˂ 1 и х 7 | И |
| 2 | (1 – х)(7 – х) 0 | 2 ˂ х ˂ 8 | А |
| 3 | (х – 2)(5 + х) 0 | х ˂-5 и х 2 | М |
| 4 | х 2 – 5х 0 | х ˂ 0 и х 5 | О |
| 5 | 2х – 5х 2 | х ˂ 2 | С |
| 6 | (х – 2)(2х - 3)2 | 0 ˂ х ˂ 2,5 | Р |
| 7 | (– х 2 + 9)(5х + 2) 0 | х 2 | Г |
| 8 | (х 2 – 4)(х +2) 0 | х ˂-3 и -0,4 ˂ х ˂ 3 | Т |
Таблица 1
В результате заполнения таблицы возникает имя Томас Гарриот.
| 7 | 4 | 3 | 1 | 6 | 8 | 1 | 5 | 5 | 2 | 4 | 7 |
| Т | О | М | А | С | Г | А | Р | Р | И | О | Т |
В связи с этим дается краткая историческая справка.
Знаки неравенства в их современном виде придумал английский математик Томас Гарриот (1560—1621). Книга с такими обозначениями вышла после смерти автора, в 1631 году. Знаки «» являлись повёрнутыми на 90° буквами V и этим полюбились математикам (2, с.680)
3. Выполнение упражнений из учебника
№ 296 (1,3)
6. Рефлексия деятельности на уроке
Сегодня мы научились решать неравенства методом интервалов. Однако существуют более сложные неравенства — дробные. Для них тоже можно применять метод интервалов, но это тема для следующего урока.
После этого обучающимся дается индивидуальная карточка, в которой нужно подчеркнуть фразы, характеризующие работу ученика на уроке
| Урок | Я на уроке | Итог |
| 1. интересно | 1. работал | 1. понял материал |
| 2. скучно | 2. отдыхал | 2. узнал больше, чем знал |
| 3. безразлично | 3. помогал другим | 3. не понял |
7. Домашнее задание
§ 16, № 297(2,4), 298(2,4)