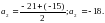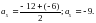План-конспект урока алгебры в 9 классе
учителя математики Середкиной Ирины Викторовны
МБОУ «Гимназия№9» г. Симферополь Республика Крым
по учебнику «Алгебра – 9» Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков,
С. Б. Суворова; под редакцией С. А. Теляковского.
Тема: Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.
Цель: ввести понятия арифметическая прогрессия арифметической прогрессии. Вывести формулы n-го члена арифметической прогрессии. Вывести и сформулировать свойство арифметической прогрессии. Выработать умения применять выведенные формулы при решении упражнений.
Задачи урока:
1. Формировать умения решать задачи, используя формулу n-го члена и основное свойство арифметической прогрессии.
2.Формировать умения делать выводы.
3. Развивать математическую речь при комментировании решения заданий.
4. Развивать творческую активность учащихся.
5. Продолжить работу над развитием логического мышления, умением анализировать, сопоставлять и обобщать полученные знания
Тип урока: урок усвоения новых знаний
Оборудование: учебник, компьютер, плазменный экран, учебная презентация Power Point.
Ожидаемые результаты: учащиеся должны усвоить определение арифметической прогрессии, какое число называют разностью арифметической прогрессии, основное свойство и формулу n-го члена арифметической прогрессии. Приводить примеры арифметических прогрессий. Уметь применять формулы при решении задач.
Ход урока.
1. Организационный момент.
2. Проверка домашнего задания.
3. Объяснение нового материала.
Задание 1. Учащимся предлагаются три последовательности:
1; 2; 3; 4;…
1; 3; 5; 7; …
2; 7; 12; 17…
и дается задание указать закон, по которому можно вычислить каждый следующий член через предыдущий.
Такие последовательности называются арифметическими прогрессиями. Учащимся предлагается сформулировать определение арифметической прогрессии.
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
(аn) – арифметическая прогрессия, n  N.
N.
аn+1 = аn + d, где d – некоторое число
d = аn+1 - аn - разность арифметической прогрессии.
Учащимся предлагается сформулировать определение разности арифметической прогрессии. И определить как влияет разность арифметической прогрессии на возрастание (убывание) прогрессии.
Задание 2. Определите, какие из предложенных последовательностей являются арифметическими. Найдите разность арифметической прогрессии.
а) 1; 2; 4; 9; 16; …
б) 1; 13; 25; 27; …
в) -4; -6; -8; -10; …
г) 3; 9; 27; 81; …
д) 3; 3; 3; 3; …
Как вы думаете, что нужно знать, чтобы задать арифметическую прогрессию? После обсуждения вопроса решить № 575(а,б) для отработки умения находить члены арифметической прогрессии по первому члену и разности.
Задание 3. Используя определение арифметической прогрессии, выразите первые пять членов через первый член и разность. Сделайте вывод.
a2 = a1+ d,
a3 = a2+ d = ( a1+ d) + d = a1+ 2d,
a4 = a3+d = (a1+2d) + d = a1+3d,
a5 = a4+ d = (a1+3d) + d = a1+4d,
………………………………….
an = a1+(n-1) d - формула n-го члена арифметической прогрессии.
4. Формирование умений и навыков.
Решение заданий на отработку применения формулы n-го члена арифметической прогрессии.
Решить устно №576(1 строчка); №577(а).
Решить письменно: №578; №579(а); №581
№ 576 (1 строчка) Дано: (вn) - арифметическая прогрессия, в1, d.
Выразить: в7 ; в231; вк+5.
Решение:
в7 = в1 + 6d; в231 = в1 + 230d; вк+5 = в1 + (к+4)d.
№577(а) Дано: (сn) - арифметическая прогрессия, с1= 20, d = 3.
Найти: с7.
Решение:
с5 = с1 + 4d; с5 = 32.
Ответ: с5 = 32.
№578. а) Дано: (an) - арифметическая прогрессия, а1= -3, d = 0,7.
Найти: а11
Решение:
а11 = а1 +10d а11 = -3 + 10∙0,7
а11 = 4
Ответ: а11 = 4.
б) Дано: (an) - арифметическая прогрессия, а1= 18, d = - 0,6
Найти: а26
Решение:
а26 = а1 +25d а26 = 18 + 25 ∙ (- 0,6)
а26 = 3
Ответ: а26 = 3.
Физминутка.
Дана арифметическая прогрессия а1; а2; а3; …; аn-1; аn; а n+1; …
Выразите разность арифметической прогрессии через аn-1, аn и через аn, а n+1.
d = an+1 – an, d = an– an-1
an– an-1 = an+1 – an;
2an = an-1 + an+1;
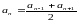 .
.
Мы вывели свойство арифметической прогрессии. Сформулируйте полученное свойство. Учащиеся дают свои формулировки данного свойства. Затем читаем формулировку из учебника стр.149.
Вопрос учащимся. Почему в данном утверждении сказано начиная со второго члена, а не с первого?
Верно и обратное утверждение: если в последовательности каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.
Далее проверяем, верно, ли это утверждение (используя материал учебника стр.150).
Задание 3. Найти неизвестные члены арифметической прогрессии
-21; а2; -15; -12; а5; -6; … .
Решение:
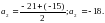
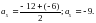
Ответ: а2 = -18, а5 = -9.
5. Итоги урока.
Вопросы учащимся:
1. Сформулируйте определение арифметической прогрессии.
2. Какое число называют разностью арифметической прогрессии?
3. Приведите примеры арифметических прогрессий.
4.Назовите формулу n-го члена арифметической прогрессии.
5.Как выражается любой член арифметической прогрессии, начиная со второго, через предыдущий и последующий члены?
Домашнее задание. Учить теорию п.25. Решить: № 575(г); №577(б); №580(б).
Литература:
1.Учебник Алгебра 9. Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В.Суворова; под редакцией С. А. Теляковского. Издательство «Просвещение», 2014.
2. Алгебра 9 класс Поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.В.Суворовой Авторы составитель С.П.Ковалева. Издательство «Учитель», 2008.






 N.
N.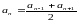 .
.