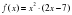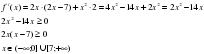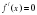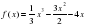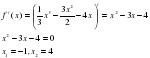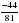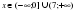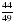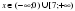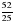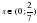| Урок |
| АЛГЕБРА 11 |
| Тема: Правила вычисления производных |
| Основные цели и задачи урока | - Закрепить знание правил вычисления производных и отработать навыки применения правил вычисления производных при решении примеров. – закрепить в сознании учащихся правила дифференцирования, совершенствование вычислительных навыков – воспитание стремления к совершенствованию знаний, формирование чувства ответственности за результат работы, развитие культуры коллективного общения, способности отстаивать свое мнение, признавать свои ошибки.– развитие познавательного интереса, внимательности и наблюдательности. |
| Ожидаемые результаты освоения темы | Учащиеся знают правила вычисления производной, понимают и Применяют правила дифференцирования, при решении примеров, совершенствование вычислительных навыков. |
| Ключевые идеи урока | Новые подходы в преподавании и обучении, - диалоговое обучение, - обучение тому, как обучаться, Оценивание для обучения и оценивание обучения. Формативное оценивание учащихся (похвала, одобрение, предложение, совет, аплодисменты), рефлексия. Обучение критическому мышлению. Управление и лидерство в преподавании, ИКТ. Обучение талантливых и одарённых детей. Преподавание и обучение в соответствии с возрастными особенностями |
| Тип урока | урок комплексного применения ЗУН учащимися |
| Методы обучения | Наглядный (презентация), словесный (беседа, объяснение), практический, частично -поисковый |
| Формы организации учебной деятельности учащихся | фронтальная; групповая; индивидуальная. |
| Используемые интерактивные методы обучения | Взаимооценивание, самооценивание, групповая работа, индивидуальная работа |
| Применение модулей | Обучение тому, как обучаться, Обучение критическому мышлению, Оценивания для обучения, Использование ИКТ в преподавании и обучения, возрастные особенности |
| Оборудование и материалы | Учебник, Интерактивная доска, индивидуальные карточки, ватман, кубик Блума, Ключи МУДРЕЦА |
| Этапы урока | ХОД УРОКА
| Прогнозируемые результаты |
| Создание коллоборативной среды Цель, которая должна быть достигнута учащимися на данном этапе урока: подготовиться к продуктивной работе на уроке.
Цель, которую хочет достичь учитель на данном этапе урока: подготовить учащихся к мыслительной деятельности, чётко организовать последующую работу.
Задачи: создать доброжелательную атмосферу урока, положительный эмоциональный настрой, обеспечить быстрое включение учащихся в деловой ритм.
Методы: словесный, наглядный | Организационный момент. (Приветствие учащихся, определение отсутствующих, проверка готовности учащихся к уроку, организация внимания).
Деление по группам. «Колечки». 1,5/
Постановка цели урока. 1,5/ Здравствуйте ребята! Предлагаю Вам отгадать ключевое слово нашего занятия. «Мозговой штурм». Даю несколько подсказок: С её появлением математика перешагнула из алгебры в математический анализ; Ньютон назвал её флюксией и обозначал точкой; Бывает первой, второй, третьей и...; Обозначается штрихом. Да, действительно тема нашего занятия - производная! А именно, на прошлом уроке мы изучали тему «Правила вычисления производной», как вы думаете, что мы будем делать на этом уроке?
Итак, тема нашего урока «Правила вычисления производных» Какую цель мы ставим к данному уроку? | Полная готовность класса и оборудования урока к работе; быстрое включение класса в деловой ритм, организация внимания всех учащихся
- отрабатывать навыки нахождения производных, повторять формулы, и т. д.
-закрепить знания правил вычисления производных, отработать навыки решения примеров на нахождение производных. |
| Основная часть урока:
Цель, которая должна быть достигнута учащимися на данном этапе урока: проверить формулировки правил вычисления производной, правильность ее применения при решений работ, физический смысл производной Цель, которую хочет достичь учитель на данном этапе урока: разобрать правила вычисления производной, решение примеров на физический смысл производной,, обратить внимание учащихся на характерные ошибки, правильность оформления работы. Задачи: установить правильность и осознанность выполнения всеми учащимися задания на правила вычисления производной; устранить в ходе проверки обнаруженные пробелы в знаниях, совершенствуя при этом ЗУН. Методы: словесный, наглядный
| Для начала повторим формулы: Прием «Ключи мудреца». 4/. Записать правила вычисления производной и приведите примеры на данные правила: 1 группа: Производная суммы и разности, степени. 2 группа: Производная произведения и частного, (kx+b)/= 3 группа: Найдите производную функции: С/= (Сu)/= x/= 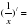 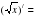 ВЗАИМООЦЕНИВАНИЕ ГРУПП по критериям: максимальный балл- 4 балла, 1/ А) точность формулы; Б) правильность примера; В) ясность ответа; Г) оформление.
Для начала мне хотелось бы узнать, вызвала ли домашняя работа у кого-нибудь затруднения.
Урок, я бы хотела, продолжить оригинальным приёмом педагогической техники «Кубик Блума». На гранях кубика написаны начала вопросов: 1) «Почему», 2) «Объясни», 3) «Назови», 4) «Предложи», 5) «Придумай», 6) «Поделись» «Почему»:5/ чему равна скорость материальной точки (м/с) в момент времени t=4м/с. Если известно, что материальная точка движется прямолинейно по закону 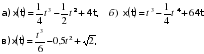 где х — расстояние от точки отсчета в метрах, t — время в секундах с начала движения. где х — расстояние от точки отсчета в метрах, t — время в секундах с начала движения. 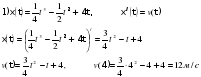 ответ: v(4)=12 м/сек ответ: v(4)=12 м/сек
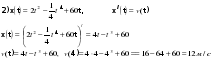
ответ: v(4)=12 м/сек
| Учащиеся находят правильный «ключ мудреца» и защищают. ВЗАИМООЦЕНИВАНИЕ ГРУПП по критериям: А) точность формулы; Б) правильность примера; В) ясность ответа; Г) оформление.
Получают соответствующее задание и выполняют тетрадях.
Пример1 решаем на доске, проверка . 2 пример на слайде. Самооценивание Правильный пример -2 балла,
Краткие исторические сведения для учащихся. |
|
Цель, которая должна быть достигнута учащимися на данном этапе урока: проверить правильность выполнения домашней работы Цель, которую хочет достичь учитель на данном этапе урока: разобрать решение домашних примеров, обратить внимание учащихся на характерные ошибки, правильность оформления работы. Задачи: установить правильность и осознанность выполнения всеми учащимися домашнего задания; устранить в ходе проверки обнаруженные пробелы в знаниях, совершенствуя при этом ЗУН. Методы: словесный, наглядный
| 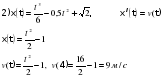 ответ: v(4)=12 м/сек САМООЦЕНИВАНИЕ ПО КРИТЕРИЯМ:1/ 1)Верное вычисление производной – 1 балл 2) Правильное решение задания -2 балла
2) «Объясните» 5/ как вы выполнили домашнее задание. Разбор заданий домашней работы. 5/ № 186. Найдите производные функций: 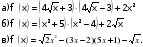
РЕШЕНИЕ: 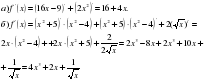
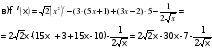
№ 190. Решите неравенство: 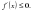 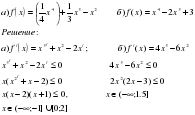 САМООЦЕНИВАНИЕ, каждый правильный пример 1 балл, всего 5 баллов. САМООЦЕНИВАНИЕ, каждый правильный пример 1 балл, всего 5 баллов.
3)«Назовите»: правильный ответ (те ст)-5/ 1) чему равно значение производной в точке х0=-2, если 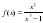
|
Ответы учащиеся, записывают домашнее задание на доске Класс проверяет домашнюю работу
Самооценивание: максимум 5 баллов
Выполняют тест, самооценивание : каждый правильный ответ 1 балл
|
|
Цель, которая должна быть достигнута учащимися на данном этапе урока: проверить правильность выполнения тестовой работы Цель, которую хочет достичь учитель на данном этапе урока: разобрать решение тестовых заданий, обратить внимание учащихся на характерные ошибки, правильность оформления работы. Задачи: установить правильность и осознанность выполнения всеми учащимися тестового задания; устранить в ходе проверки обнаруженные пробелы в знаниях, совершенствуя при этом ЗУН. Методы: словесный, наглядный
| 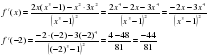 2) чему равно решение неравенства 2) чему равно решение неравенства 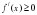 , если , если 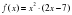
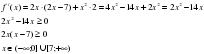
3) чему равен корень уравнения 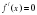 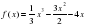
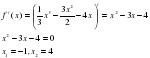
Таблица ответов | № | 1 | 2 | 3 | | А | 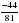
|
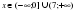
| -1; -4 | | В | 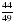
|
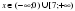
| -1; 4 | | С | 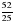
| 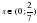
| -1;3 | | D | 
|

| Нет решения | | E | 
| 
| 1;-4 |
Каждый правильный ответ 1 балл |
Выполняют тест А Е В
|
|
Цель, которая должна быть достигнута учащимися на данном этапе урока: проверить правильность применения правил дифференцирования Цель, которую хочет достичь учитель на данном этапе урока: разобрать решение индивидуальных заданий, обратить внимание учащихся на характерные ошибки, правильность оформления работы. Задачи: установить правильность и осознанность выполнения всеми учащимися индивидуального задания; устранить в ходе проверки обнаруженные пробелы в знаниях, совершенствуя при этом ЗУН. Методы: словесный, наглядный
Историческая справка (Обучение талантливых и одарённых детей) Цель, которая должна быть достигнута учащимися на данном этапе урока: познакомиться с историческими фактами, рассказывают учащиеся.
| 4) «Предложите», -4/ хотя бы одну функцию, производная которой равна: а) 12х3+7, б) 3х2- , , в)  5) «Придумайте», 5 примеров на вычисление производной с решением , параграф 13, заполнить таблицу «ЗХУ», запись домашнего задания в дневник -1/ 6) «Поделитесь» новой информацией. Творческая работа: (выступление учащихся) 10/ (индивидуальные задания) Пример №1. Найти производную функции у=х5-4х3+2х2-7х Решение: у/ =(х5-4х3+2х2-7х)/=5х4-12х2+4х-7
Пример №2. Найти производную функции у=(1-х3)(х4+4х) Решение: у/=(1-х3)/ (х4+4х)+ (1-х3)(х4+4х)/=-3х2(х4+4х)+ (1-х3)(4х3+4)=-3х6-12х3+4х3+4-4х6-4х3=-7х6-12х3+4
Пример №3. Найти производную функции  Решение:
Жазира: Слово математика, возникла в Древней Греции примерно в  веке до н.э. Происходит она от слова, что в переводе означает «учение» «знания полученные через размышления». Термин веке до н.э. Происходит она от слова, что в переводе означает «учение» «знания полученные через размышления». Термин «Дифференциал» в переводе с латинского означает «разность».
|
А) у=3х4+7х Б) у=х3+ В)  Каждый правильный ответ -1 балл, всего 3 балла.
Выполняют индивидуальные задания
Задание творческого характера
|
| Цель, которую хочет достичь учитель на данном этапе урока:
воспитывать интерес к предмету математики, содействовать осознанию учащимися ценности изучаемого предмета. Задачи: создать доброжелательную атмосферу урока, положительный эмоциональный настрой, закрепить некоторые математические понятия по теме «Производная». Методы: словесный, наглядный
|
Малика: Жозеф Луи Лагранж (25.01.1736 – 10.04.1813) -французский математик, астроном и механик. Внёс огромный вклад в математический анализ, теорию чисел, в теорию вероятностей и численные методы, Лагранж ввёл обозначения y ' и f ' (x) и для производной.
Анна: Ньютон Исаак(1643-1727)-великий английский ученый. Одновременно с Г.Лейбницем разработал основы математического анализа. Создатель классической механики. Ньютон, ученый, который пришел к открытию дифференциального исчисления при решении задач о мгновенной скорости движения материальной точки.
Роза: Лейбниц Готфрид Фридрих (1646-1716)-великий немецкий ученый. Философ, математик, физик, юрист, языковед. Создатель (наряду с Ньютоном) математического анализа. Основоположник большой математической школы. Идеи Лейбница оказали значительное влияние на развитие математической логики. Это математик, который пришел к открытию дифференциального исчисления при решении задач о построении касательной к любой кривой, заданной своим уравнением
|
|
| Рефлексия | Подведение итога Домашнее задание: ПРИДУМАТЬ 5 ПРИМЕРОВ НА ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ, ПАРАГРАФ 13, ЗАПОЛНИТЬ ТАБЛИЦУ «ЗХУ» РЕФЛЕКСИЯ-1,5/ Прием «Благодарю…»: В конце урока предлагаю каждому ученику выбрать только одного из ребят, кому хочется сказать спасибо за сотрудничество и пояснить, в чем именно это сотрудничество проявилось. СПАСИБО ЗА УРОК1 | Отзывы ребят. |







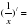
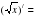
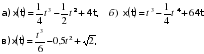 где х — расстояние от точки отсчета в метрах, t — время в секундах с начала движения.
где х — расстояние от точки отсчета в метрах, t — время в секундах с начала движения. 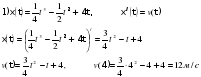 ответ: v(4)=12 м/сек
ответ: v(4)=12 м/сек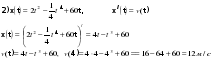
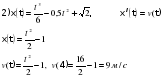
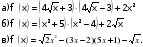
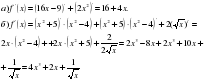
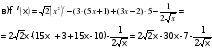
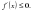
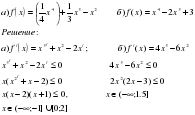 САМООЦЕНИВАНИЕ, каждый правильный пример 1 балл, всего 5 баллов.
САМООЦЕНИВАНИЕ, каждый правильный пример 1 балл, всего 5 баллов.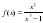
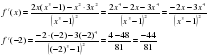 2) чему равно решение неравенства
2) чему равно решение неравенства 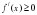 , если
, если