Конспект урока по геометрии 8 класс

8 класс 13.01.2018

Урок № 33
ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ

(первый признак подобия треугольников)

Цели:

• создать условия для формирования умений формулировать, доказывать и применять первый признак подобия треугольников при решении задач.

Задачи:

обучающие:   

• изучение способов доказательства первого признака подобия треугольников и рассмотреть способы применения этого признака при решении задач,  получение знаний по теме, умение применять их в практической   деятельности, расширение границ и возможностей образовательных компетенций учащихся.

 развивающие:     

• развитие умений и навыков у учащихся решения задач, осуществление контроля с диагностикой ошибок и с обратной связью, развитие самостоятельности и успешности.

 воспитательные:      

• формирование культуры познавательной деятельности;

• развитие у учащихся  самостоятельности, внимательности;

• воспитание интереса к математике.

Ход урока

1. Организационный момент

2. Актуализация опорных знаний

1. Какие треугольники называются подобными?

2. Какие стороны треугольников называются сходственными?

3. Чему равно отношение площадей подобных треугольников?

4. .... А отношение их периметров?

5. Чему равно отношение площадей треугольников, имеющих равные углы?

3. Решение задач по готовым чертежам

Устное решение задач (задачи по готовым чертежам) (Слайды 3,4,6,7)

Задача 1 Рис.1

АВСА₁В₁С₁. Найти х и у

Решение

Так как АВС  А₁В₁С₁ и С = С₁, А = А₁, В = В₁то АВ и А₁В₁, ВС и В₁С₁, АС и А₁С₁ – соответственно сходственные стороны.

Если k – коэффициент подобия, тогда k =, следовательно В₁С₁ = х = 5 * 1,5 = 7,5,

АС = у = 10,5 : 1,5 = 7

Задача 2 Рис.2

АВС  А₁В₁С₁. Найти х , у и z.

Решение

Так как АВС А₁В₁С₁ , то k = p/p₁ = 27/9 = 3, значит х = 8/3у = 3, z = 

Задача 3 Рис.3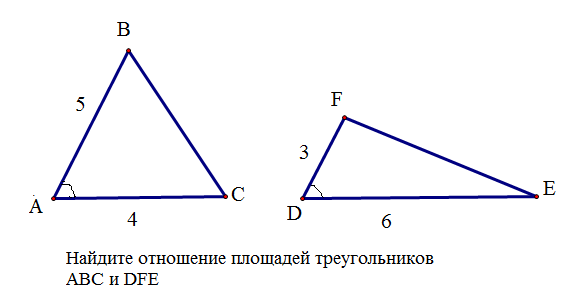

Решение.

Так как А = D, 

Задача 4 Рис.4

S_АОВ = 20. Найти S_COD.

Решение

Так как АОВ = СОD, то 

Следовательно S_COD = 20 : 4 = 5

4. Изучение нового материала (слайд №8).

Учитель предлагает формулировку теоремы, отражающей признак подобия треугольников по двум углам. В беседе с учащимися уточняется, что в теореме дано и что нужно доказать.

Далее восьмиклассники cамостоятельно выполняют доказательство теоремы на заранее приготовленных листах (смотри приложение 1), в которых предлагается заполнить пропуски в формулировке и доказательстве первого признака подобия треугольников.

5. Устное решение задач на закрепление нового материала

Рис.4   Рис. 5

Докажите, что треугольники подобны и укажите их сходственные стороны (слайды 9, 10)

Рис. 6

CQP = A, BC = 18 см, CP = 6 см, CQ = 4 см

Найдите АС. (слайд 11)

6. Зарядка для глаз. (слайды с 12 по 17)

7. Письменное решение задачи № 551(б) (слайд. 12)

Учитель обращает внимание на оформление решения задачи

Рис. 7

Дано: ABCD - параллелограмм

АВ = 8 см, AD= 5см, CF=2см

Найти DЕ и ЕС

Решение

1. ADE FCE (по двум углам), так как

AED = FEC (по свойству вертикальных углов) , EDA = ECF (по свойству накрест лежащих углов при AD || BC и секущей CD)

Следовательно 

8. Самостоятельная работа

Ребятам предлагается в парах обсудить и записать краткое решение и ответ в задачах из Сборников подготовки к ГИА по математике (модули “Реальная математика” и “Геометрия” (часть 2)

I вариант:

Пример задачи № 17 из модуля “Реальная математика” ГИА по математике Сосна высотой 2 м отбрасывает тень длиной 3 м. Найдите рост человека (в метрах), стоящего около сосны, если длина его тени равна 0,4 м

II вариант:

Пример задачи № 17 из модуля “Реальная математика” ГИА по математике

На сколько метров поднимется прикреплённый к колодезному журавлю конец верёвки, если человек опустил короткий конец журавля на 80 см? Плечи журавля составляют 2 м и 6 м.

Дополнительная задача:

Пример задачи № 25 из модуля “Геометрия” (часть 2) ГИА по математике

Угол В треугольника АВС в 2 раза больше угла А. Биссектриса угла В треугольника пересекает сторону АС в точке D. Докажите, что треугольник АВС подобен треугольнику ВDС.

9. Итог урока

В чём заключается первый признак подобия треугольников?

Сформулируйте возможный алгоритм решения задач на подобие треугольников

Возможный ответ учащихся:

А) Находим пару предполагаемых подобных треугольников.

Б) Доказываем, что эти треугольники подобны, используя признак подобия треугольников.

В) Определяем сходственные стороны треугольников и составляем соответствующую пропорцию.

С) Находим неизвестные члены этой пропорции.

10. Домашнее задание: _____________________________________________

____________________________________________________________________________________________________________________________________

11. Рефлексия

• Что нового вы узнали на уроке?

• На сколько трудным вам показался материал?

• Какую оценку вы бы себе поставили за работу на уроке?

4. Итоги урока

1. Для того чтобы записать пропорциональность сторон подобных треугольников, нужно:

1) выяснить, при каких вершинах углы равны;

2) определить, какие стороны являются сходственными (лежат против равных углов);

3) записать пропорцию, где в числителях – стороны одного треугольника, в знаменателях – сходственные им стороны другого.

2. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам.

Домашнее задание: ________________________________________________

____________________________________________________________________________________________________________________________________

вопросы 1–5, с. 160; №№ 551 (б), 552 (а), 553 (б).

П. 59, вопр. 1-5 (стр. 160) № 550, 552(а), 553

Для желающих.

На чертеже изображен шлагбаум, закрывающий проезд через железнодорожное полотно. На сколько опустится короткий конец шлагбаума, если больший поднимается на 2 м?