Тема занятия: Многогранник и геометрическая гирлянда
Цели:
Личностные: способствовать развитию умения слушать, ясно, точно, грамотно излагать свои мысли, развивать креативность мышления, инициативу, находчивость.
Познавательные: развивать способность к восприятию математических понятий, логических рассуждений, способов решения задач, рассматриваемых проблем; способность видеть математическую задачу в других дисциплинах (биологии, литературе)
Регулятивные: способствовать развитию умений к самоконтролю и результату учебной математической деятельности; пониманию и удерживанию цели на протяжении всего занятия.
Коммуникативные: создать условия для формирования умений работать в паре, группах, вести диалог;
Предметные: использовать геометрический язык для описания предметов окружающего мира; исследовать и описывать свойства правильных многогранников, используя эксперимент, наблюдение, измерение. Моделировать геометрические объекты, используя развертки фигур, изучать свойства тел, используя готовые модели.
Оборудование: мультимедиапроектор, экран, компьютер, доска, развертки фигур, демонстрационные модели многогранников и правильных многогранников
Основные понятия: правильные многогранники, грань, ребро, вершина, тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр.
Вид занятия - занятие-исследование
ХОД ЗАНЯТИЯ
Организационный момент. Положительный настрой на занятие
Добрый день, ребята! Я очень рада сегодняшней встрече с вами!
Поприветствуем друг друга
Собрались ребята в круг,
Слева друг и справа друг.
Вместе за руки возьмёмся
И друг другу улыбнёмся.
Я передаю улыбку Алене, Алена передаёт …..
- А теперь передадим улыбку нашим гостям.
И с хорошим настроением начнем наше занятие
2. Мотивационный этап.
Уч. – Чем будем заниматься сегодня на занятии?
Д. (все) - Сегодня мы будем вновь наблюдать,
Выводы делать и рассуждать.
Уч. – Чтобы всё получилось удачно – работаем как всегда под девизом:
Все: - «Сделай сам, помоги другому».
Ребята, посмотрите на окружающий нас мир, мир в котором мы с вами живем неразрывно связан с геометрией. Очень важно уметь смотреть и видеть, замечать различные особенности окружающего мира и делать выводы. Чтобы хорошо владеть этой наукой нужно постоянно развивать логическое мышление, чем мы сейчас и займемся, решая ребусы.
Уч. – Итак, приведём наш ум в рабочую готовность.
3 . Задания на логическое мышление (Ответы высвечиваются на слайде)
Разгадайте ребусы: пирамида, параллелепипед, квадрат, трапеция, четырехугольник, многогранник)



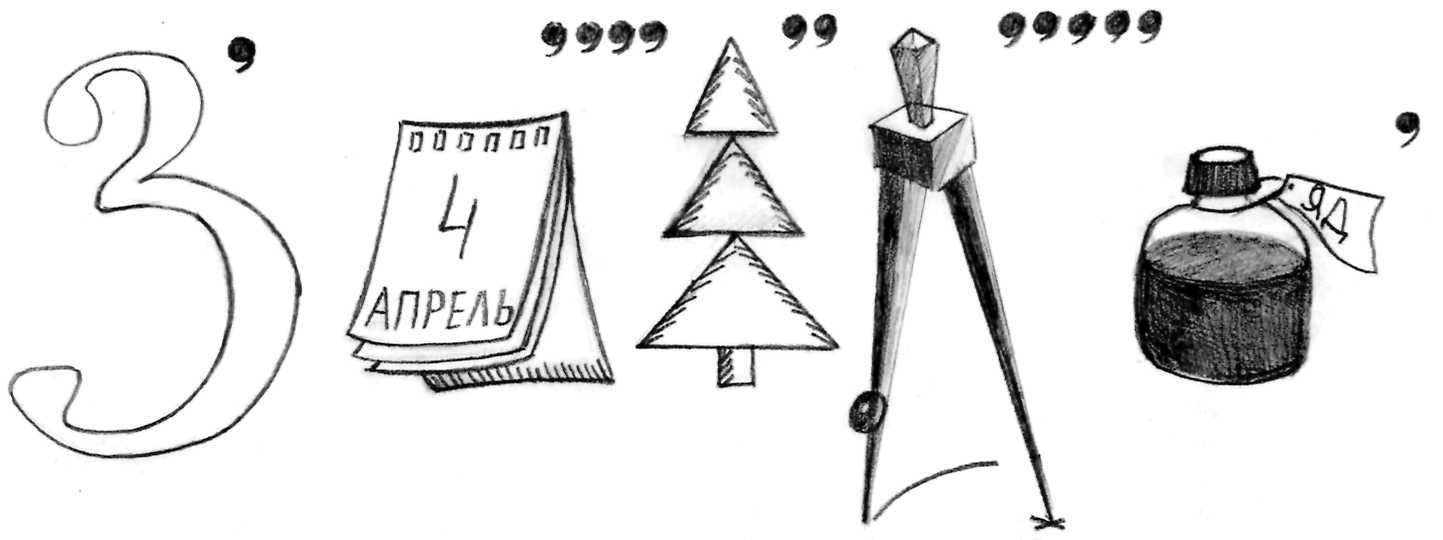







 6 = Ё 1 = Г
6 = Ё 1 = Г 
Каким одним словом можно объединить эти слова? (Геометрические фигуры)
Ключевое слово Ребус «Многогранник», которое поможет нам определить тему нашего занятия
А еще я предлагаю вам отгадать загадку:
2.Декоративное украшение, цепочка соединѐнных между собой нитью/проводом предметов (ветвей, цветов, лампочек, фонариков и т. д.), применяемое для украшения праздников. (Гирлянда).
А так как мы говорим о геометрических фигурах, то речь пойдет как вы думаете о какой гирлянде (о геометрической гирлянде (фото на слайде)
- А теперь попробуем сформулировать тему нашего занятия (предложения детей).
Тема нашего занятия: МНОГОГРАННИК И ГЕОМЕТРИЧЕСКАЯ ГИРЛЯНДА.
4. Подготовка учащихся к усвоению нового материала.
Класс разбивается на пары. Раздаются конверты с многоугольниками:
А сейчас проведем геометрический тренинг. Выполняя это задание, вы познакомитесь с разными видами многогранников.
Какие многоугольники вы знаете?
-Классифицируйте их по каким либо признакам (правильные и неправильные многоугольники)
Вопросы:
Посмотрите внимательно и скажите, что у них общего или чем отличаются? (У одних длины сторон равны, у других - разные) (Плоские фигуры)

Какой многоугольник называется правильным?
Ответ: многоугольник называется правильным, если все стороны и все углы у него равны
Учитель: Какая же связь темы нашего занятия «Многогранник» с многоугольниками. Давайте сформулируем цели нашего занятия.
Сообщение целей занятия.
1.Научиться отличать многоугольники от многогранников.
2.Дать понятие правильных многогранников и уметь их называть.
3.Рассмотреть свойства правильных многогранников.
4. Изготовить геометрическую гирлянду, используя развертки многогранников.
Как вы думаете, какую фигуру можно назвать многогранником?
Возможно, нам в этом поможет набор этих замечательных моделей.(демонстрация моделей многогранников)
Рассмотрите, пожалуйста, модели этих тел.
-Какое сходство они имеют с многоугольниками, о которых только что шла речь? (Стороны имеют форму треугольника, квадрата, пятиугольника)
-В чем разница между многоугольниками и многогранникам? (плоские фигуры и объемные тела)
Так что же представляют собой эти столь совершенные тела?
И возможно ли обойтись без многогранников?
На эти вопросы мы постараемся сегодня ответить.
- Давайте вместе попытаемся дать определение МНОГОГРАННИКА
СЛАЙД
Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями.
Стороны граней – рёбра многогранника, а концы рёбер – вершины многогранника. По числу граней различают четырёхгранники, пятигранники и т. д.
Особое место среди многогранников занимают правильные многогранники.
СЛАЙД Правильным называется многогранник, у которого все грани являются правильными многоугольниками, все многогранные углы при вершинах равны, в каждой его вершине сходится одинаковое число ребер.
Итак, еще раз повторим определение многогранника
-Что является гранью многогранника?(плоские правильные многоугольники)
-Что является ребром? (сторона грани)
КАКУЮ ЦЕЛЬ мы ставили перед собой?
(научиться отличать многоугольник от многогранника)
СЛАЙД. Задание: на слайде: Под какими номерами находятся многоугольники, а под какими – многогранники) Если согласны-сигналят
(СИГНАЛЬНЫЕ КАРТОЧКИ)
МОЛОДЦЫ! Достигли мы цели?
Научились отличать многоугольник от многогранника?
КАКУЮ ЦЕЛЬ СТАВИЛИ ЕЩЕ?
(Узнать как называются многогранники)
Итак, внимание! К нам пришло письмо (в конверте). Послушайте, пожалуйста, о чем в нем говорится
Однажды обыкновенный мальчик Джеймс, увлекшись изготовлением моделей многогранников, написал в письме к отцу: «… я сделал тетраэдр, додекаэдр и еще два эдра, для которых не знаю правильного названия». Эти слова знаменовали рождение, в пока ничем не примечательном мальчике великого физика Джеймса Клерка Максвелла, который впоследствии сделал немало важных открытий в физике.
Вопрос: О чем идет речь в данном письме? (О многогранниках)
Что вам показалось новым, а что уже знакомо? (Что такое эдра)
Что в переводе с греческого означает слово «ЭДР»?
Оказывается, что правильных многогранников ровно пять - ни больше, ни меньше.
СЛАЙД
 .
.
Названия многогранников пришли из Древней Греции, в них указывается число граней: «эдра» - грань; «тетра» - 4; «гекса» - 6; «окта» - 8; «додека» - 12, «икоса» - 20. В дословном переводе с греческого "тетраэдр", "октаэдр", "гексаэдр", "додекаэдр", "икосаэдр" означают: "четырехгранник", "восьмигранник", "шестигранник", "двенадцатигранник", "двадцатигранник". Этим красивым телам посвящена 13-я книга "Начал" Евклида.
СЛАЙД (На столах памятки- таблица с названиями многогранников)
| «эдра» | грань | Пример |
| «тетра» | 4 | 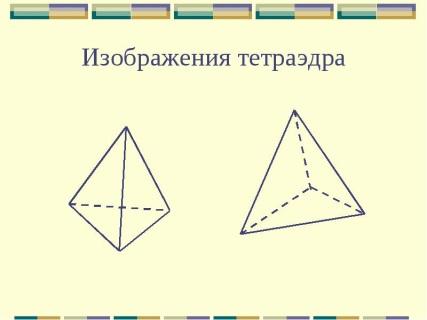
|
| «гекса» | 6 | 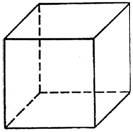
|
| «окта» | 8 | 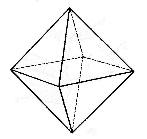
|
| «додека» | 12 | 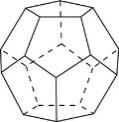
|
| «икоса» | 20 | 
|
"Правильных многогранников вызывающе мало, - написал когда-то Л. Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".
ПОКАЗ СЛАЙДОВ (многогранники в различных науках(1-4)
И кубики, которыми играют дети, и объекты архитектуры и дизайна, и предметы обихода состоят из правильных многогранников.
Например, египетские пирамиды, и самая известная из них – пирамида Хеопса. (слайд). Это правильная пирамида, в основании которой квадрат.
Они встречаются в природе в виде кристаллов, и в виде вирусов. А биологи говорят о том, что шестиугольные соты пчел, содержащие мед, тоже имеют форму правильного многогранника. Существует гипотеза, что именно правильная шестиугольная форма сот помогает сохранить полезные свойства этого ценного продукта.
СЛАЙД Совершенство форм, красивые математические закономерности, присущие правильным многогранникам, явились причиной того, что им приписывали различные магические свойства и все пять геометрических тел издавна были обязательными спутниками волшебников и звездочетов.
История правильных многогранников уходит в глубокую древность. Правильными многогранниками увлекались Пифагор и его ученики. Позже древнегреческий ученый Платон. Они занимали важное место в устройстве мироздания. Четыре многогранника олицетворяли в ней четыре "стихии".
Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх;
Икосаэдр - воду, т.к. он самый "обтекаемый";
куб - землю, как самый "устойчивый";
октаэдр - воздух, как самый "воздушный".
Пятый многогранник, додекаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным
Еще раз посмотрите на эти модели, потрогайте их руками, запомните названия.
Я предлагаю поиграть
ИГРА «Угадай» (проходит как физминутка)
(С завязанными глазами ученик выходит и определяет многогранник. Давайте договоримся: если правильно, вы хлопаете, если нет - топаете).
Молодцы! Продолжаем дальше наше занятие.
5. Индивидуальная работа. На доске вывешивается таблица
На партах у вас лежат модели правильных многогранников. Изучите свойства и по вашим наблюдениям заполните таблицу. (Распечатать цветным на отдельных листах фигуры многогранников, изучив информацию, заполнить таблицу )
1 группа «КУБ» (на столах лежат модели)


КУБ И ЕГО СВОЙСТВА:
куб составлен из 6 правильных четырехугольников (квадратов);
каждая его вершина является вершиной трех квадратов.
Таким образом, куб имеет: 6 граней, 8 вершин, 12 ребер.
Практическое применение куба: кубики детские, кубик – рубик
2 группа «ТЕТРАЭДР» (на столах лежат модели)
ТЕТРАЭДР И ЕГО СВОЙСТВА:
тетраэдр составлен из четырех равносторонних треугольников,
каждая его вершина является вершиной трех треугольников
Таким образом, тетраэдр имеет: 4 грани, 4 вершины, 6 ребер
Практическое применение тетраэдра: чай, тетра пакет с молоком,…
3 группа «ДОДЕКАЭДР» (на столах лежат модели)
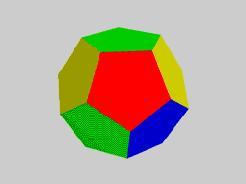

ДОДЕКАЭДР И ЕГО СВОЙСТВА:
додекаэдр составлен из 12 правильных пятиугольников,
каждая его вершина является вершиной трех пятиугольников.
Таким образом, додекаэдр имеет: 12 граней, 20 вершин, 30 ребер.
Практическое применение додекаэдра: в живописи
Сальвадор Дали «Тайная вечеря»
4 группа «ОКТАЭДР» (на столах лежат модели)
ОКТАЭДР И ЕГО СВОЙСТВА:
- октаэдр составлен из 8 равносторонних треугольников,
-каждая вершина является вершиной четырех треугольников.
Таким образом, октаэдр имеет 8 граней, 6 вершин, 12 ребер
Практическое применение октаэдра:
в головоломках, в природе, а именно в строении кристаллов алмаза.
5 группа «ИКОСАЭДР» (на столах лежат модели)
ИКОСАЭДР И ЕГО СВОЙСТВА:
- икосаэдр составлен из 20 равносторонних треугольников, -каждая вершина является вершиной пяти треугольников Таким образом, икосаэдр имеет 20 граней, 12 вершин, 30 ребер
Практическое применение: его форму имеют живые существа, одноклеточная феодария и вирусы
МОЛОДЦЫ!!!
- Мы познакомились с каждым многогранником, заполнили таблицу, а теперь заполним последний столбец. Подсчитаем число указанных элементов правильных многогранников и зафиксируем результаты в таблице 1.
| Правильный многогранник | Число граней | Число вершин | Число ребер | Г+В-Р |
| Тетраэдр | 4 | 4 | 6 | |
| Куб | 6 | 8 | 12 | |
| Октаэдр | 8 | 6 | 12 | |
| Додекаэдр | 12 | 20 | 30 | |
| Икосаэдр | 20 | 12 | 30 | |
Что вы заметили? - В последней колонке для всех многогранников получился один и тот же результат: Число граней плюс число вершин минус число рёбер равно 2.
СЛАЙД
Г + В - Р = 2
| Правильный многогранник | Сумма граней и вершин | Число ребер | (Г+В) - Р
|
| Тетраэдр | 4+4=8 | 6 | 2 |
| Куб | 6+8=14 | 12 | 2 |
| Октаэдр | 8+6=14 | 12 | 2 |
| Додекаэдр | 12+20=32 | 30 | 2 |
| Икосаэдр | 20+12=32 | 30 | 2 |
Была выведена формула, связывающая число вершин (В), граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением:
В + Г = Р + 2.
Доказал это удивительное соотношение один из величайших математиков Леонард Эйлер (1707 – 1783), поэтому формула названа его именем: формула Эйлера. Этот гениальный учёный, родившийся в Швейцарии, почти всю жизнь прожил в России, и мы с полным основанием и гордостью можем считать его соотечественником.
Самое удивительное в этой формуле, что она верна не только для правильных многогранников, но и для всех многогранников!
Сформулируем ее так: «Сумма числа граней и вершин равна числу ребер, увеличенному на 2»: Г + В = Р + 2.
Но с ней подробнее вы познакомитесь в старших классах на уроках геометрии.
Итак, какую цель мы ставили перед собой?
(Изучить свойства многогранников)
Какое основное свойство имеют многогранники?
(Сумма числа граней и вершин равна числу ребер, увеличенному на 2»: Г + В = Р + 2).
ВНИМАНИЕ! РАБОТА С ТАБЛИЦЕЙ.
Мы заполнили таблицу, посмотрите внимательно, запомните еще раз названия, постарайтесь запомнить число граней, вершин, ребер для каждого многогранника.
Я закрываю таблицу. Проверка знаний
- Сколько у тетраэдра граней? вершин, ребер?
- Сколько у гексаэдра граней? вершин, ребер?
-Сколько у октаэдра граней? вершин, ребер?
-Сколько у додекаэдра граней? вершин, ребер?
-Сколько у икосаэдра граней? вершин, ребер?
Справились с этим заданием.
Какую цель мы ставили перед собой?
(Научиться моделировать многогранники и смастерить геометрическую гирлянду)
VI. Моделирование многогранников.
Учитель: Одним из способов изготовления правильных многогранников является способ с использованием, так называемых развёрток.
Что же такое развёртка многогранника? Это модель, из которой можно свернуть данный многогранник. При этом необходимыми инструментами являются клей и ножницы.
У вас на столах листы с напечатанными развертками каждого правильного многогранника. Ваше задание: используя их, склеить модели каждого из 5 правильного многогранника.
И если вы потрудитесь над их изготовлением, то наверняка они доставят вам радость и удовольствие, а возможно принесут удачу!
Составим ГЕОМЕТРИЧЕСКУЮ Гирлянду.
Рефлексия, итог урока.
А теперь подведем итоги нашего занятия.
СЛАЙД
Давайте еще раз назовем все правильные многогранники (На СЛАЙДЕ – без названия, а ученики отвечают)
Что нового для себя узнали?
Что было интереснее всего?
На этом занятие наше завершено. Я благодарю вас за работу.














 .
.



















