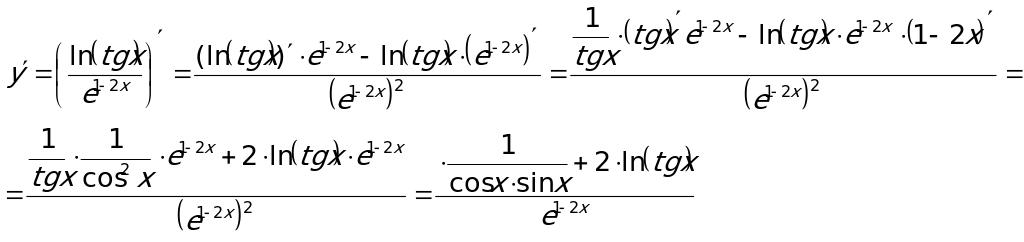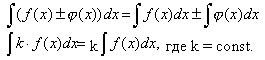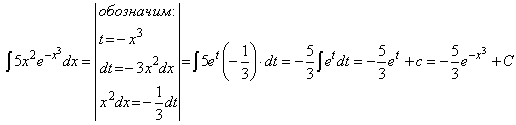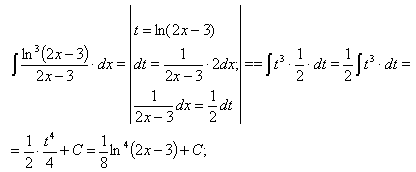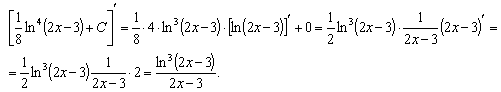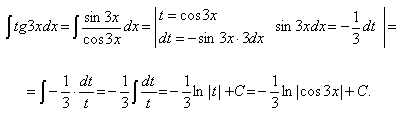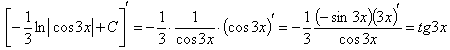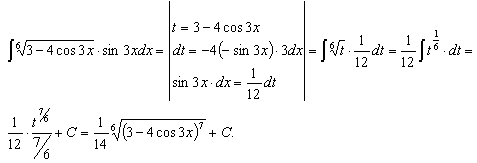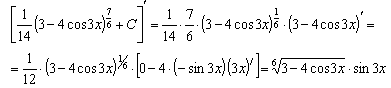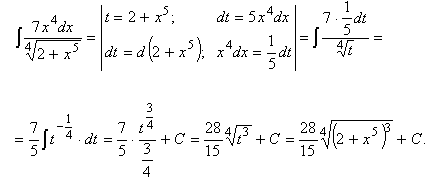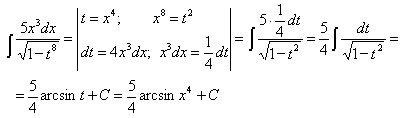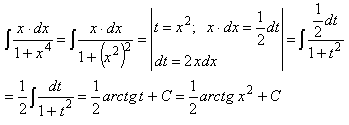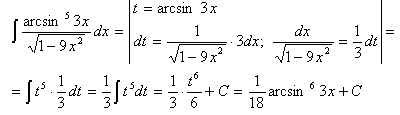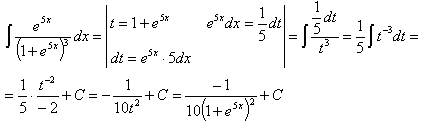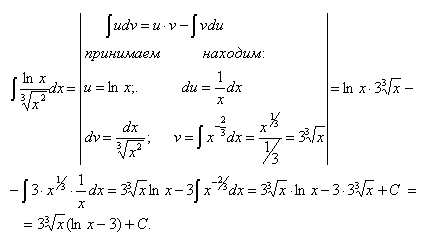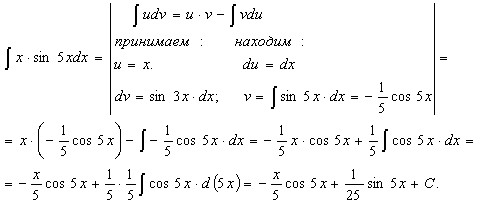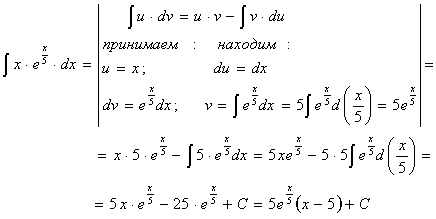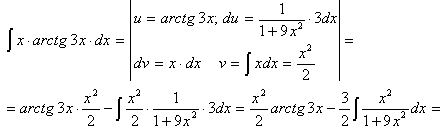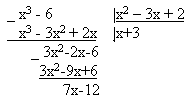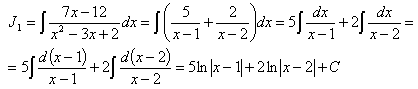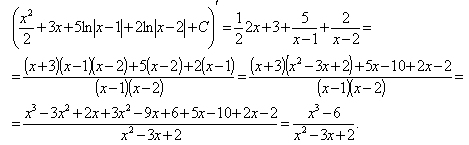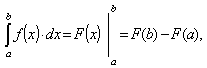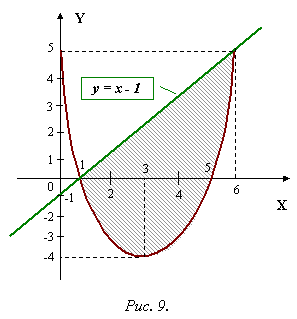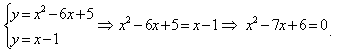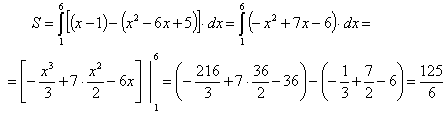ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ по математике нужно придерживаться следующих правил.
Каждую контрольную работу выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
На обложке тетради ясно написать фамилию, инициалы, учебный шифр, номер контрольной работы, название дисциплины. В конце работы указать использованную литературу, дату выполнения и расписаться.
В работу включить все задачи, указанные в задании, строго по своему варианту.
Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
Перед решением каждой задачи записать полностью ее условие.
Решения задач излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
После получения прорецензированной работы, исправить все отмеченные рецензентом ошибки и недочеты, и выполнить все рекомендации рецензента.
Если работа возвращена на доработку, то нужно выполнить указания рецензента в той же тетради в короткий срок и сдать работу на повторную проверку.
В связи с этим рекомендуется оставлять в конце тетради несколько чистых листов.
По каждой работе со студентом проводится собеседование, после чего выставляется зачет по контрольной работе.
Без зачтенных контрольных работ студент к аудиторной контрольной работе не допускается.
ПРАВИЛО ВЫБОРА ВАРИАНТА
Вариант контрольной работы определяется по таблице в зависимости от двух последних цифр номера шифра личного дела студента. В колонке таблицы по вертикали расположены цифры от 0 до 9, каждая из которых - предпоследняя цифра номера шифра. В верхней строке по горизонтали размещены так же цифры от 0 до 9, каждая из которых – последняя цифра шифра.
Пересечение вертикальной и горизонтальной линий определяет номера заданий контрольной работы. Например, по последним двум цифрам номера шифра “78” находят вариант контрольной работы на пересечении строки с цифрой 7 и столбец с цифрой 8. Для контрольной работы это номера: 4, 17, 23, 39, 47, 56
Будьте внимательны при выборе варианта. Работа, выполненная не по своему варианту, возвращается без проверки.
ТАБЛИЦА ВЫБОРА ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ № 1
|
| Последняя цифра номера шифра |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
|
П
р
е
д
п
о
с
л
е
д
н
я
я
ц
и
ф
р
а
н
о
м
е
р
а
ш
р
и
ф
т
а | 0 | 1 | 2 | 3 | 10 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 11 | 12 | 13 | 20 | 14 | 15 | 16 | 17 | 18 | 19 |
|
| 30 | 21 | 28 | 29 | 27 | 26 | 24 | 25 | 23 | 22 |
|
| 39 | 40 | 31 | 38 | 32 | 33 | 34 | 35 | 36 | 37 |
|
| 44 | 41 | 46 | 45 | 49 | 47 | 50 | 48 | 43 | 42 |
|
| 60 | 57 | 56 | 54 | 51 | 52 | 53 | 55 | 58 | 59 |
|
| . |
|
| 1 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|
| 40 | 39 | 38 | 37 | 36 | 35 | 34 | 33 | 32 | 31 |
|
| 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 41 | 42 |
|
| 54 | 56 | 55 | 60 | 57 | 53 | 51 | 58 | 59 | 52 |
|
| . |
|
| 2 | 2 | 1 | 6 | 7 | 3 | 8 | 4 | 5 | 10 | 9 |
|
| 12 | 13 | 14 | 11 | 19 | 16 | 15 | 17 | 20 | 18 |
|
| 28 | 30 | 22 | 23 | 24 | 25 | 26 | 27 | 29 | 21 |
|
| 40 | 38 | 39 | 36 | 31 | 37 | 32 | 33 | 34 | 35 |
|
| 45 | 46 | 42 | 41 | 43 | 44 | 50 | 47 | 48 | 49 |
|
| 51 | 54 | 58 | 53 | 55 | 59 | 52 | 57 | 56 | 60 |
|
| . |
|
| 3 | 9 | 10 | 7 | 6 | 5 | 4 | 3 | 1 | 8 | 2 |
|
| 19 | 18 | 20 | 17 | 16 | 15 | 14 | 12 | 13 | 11 |
|
| 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 21 | 22 |
|
| 39 | 40 | 37 | 38 | 31 | 32 | 33 | 34 | 35 | 36 |
|
| 42 | 41 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
|
| 54 | 56 | 55 | 59 | 58 | 57 | 60 | 52 | 51 | 53 |
|
| . |
|
| 4 | 3 | 2 | 1 | 4 | 5 | 7 | 9 | 10 | 6 | 8 |
|
| 13 | 17 | 15 | 16 | 14 | 12 | 18 | 11 | 20 | 19 |
|
| 27 | 29 | 30 | 21 | 22 | 24 | 25 | 26 | 28 | 23 |
|
| 31 | 33 | 32 | 34 | 35 | 36 | 39 | 37 | 40 | 38 |
|
| 46 | 45 | 47 | 48 | 50 | 49 | 41 | 42 | 43 | 44 |
|
| 51 | 56 | 57 | 54 | 55 | 53 | 60 | 52 | 58 | 59 |
|
|
| .. |
|
| 5 | 8 | 7 | 10 | 5 | 4 | 6 | 2 | 1 | 9 | 3 |
|
| 18 | 19 | 17 | 20 | 12 | 14 | 13 | 15 | 11 | 16 |
|
| 22 | 23 | 24 | 25 | 21 | 27 | 28 | 29 | 30 | 26 |
|
| 38 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 39 | 40 |
|
| 42 | 46 | 45 | 49 | 48 | 47 | 50 | 41 | 43 | 44 |
|
| 58 | 56 | 57 | 60 | 52 | 59 | 53 | 55 | 51 | 54 |
|
| .. |
|
| 6 | 7 | 6 | 9 | 10 | 3 | 2 | 1 | 8 | 5 | 4 |
|
| 17 | 18 | 19 | 16 | 20 | 11 | 12 | 14 | 13 | 15 |
|
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 22 | 21 |
|
| 37 | 38 | 31 | 32 | 33 | 34 | 35 | 36 | 40 | 39 |
|
| 49 | 50 | 48 | 47 | 41 | 42 | 43 | 44 | 45 | 46 |
|
| 54 | 55 | 58 | 56 | 60 | 52 | 59 | 53 | 51 | 57 |
|
| .. |
|
| 7 | 6 | 10 | 8 | 9 | 7 | 1 | 2 | 3 | 4 | 5 |
|
| 16 | 15 | 14 | 13 | 12 | 20 | 18 | 19 | 17 | 11 |
|
| 24 | 26 | 27 | 28 | 29 | 30 | 21 | 22 | 23 | 25 |
|
| 36 | 37 | 40 | 31 | 32 | 33 | 34 | 35 | 39 | 38 |
|
| 49 | 50 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
|
| 54 | 60 | 57 | 55 | 53 | 58 | 52 | 59 | 56 | 51 |
|
| .. |
|
| 8 | 5 | 4 | 3 | 2 | 1 | 10 | 7 | 9 | 8 | 6 |
|
| 15 | 14 | 13 | 12 | 11 | 16 | 20 | 19 | 18 | 17 |
|
| 25 | 27 | 28 | 30 | 29 | 21 | 22 | 23 | 24 | 26 |
|
| 40 | 32 | 33 | 34 | 35 | 36 | 37 | 31 | 38 | 39 |
|
| 48 | 47 | 50 | 49 | 44 | 45 | 46 | 41 | 43 | 42 |
|
| 51 | 55 | 60 | 52 | 59 | 57 | 53 | 58 | 56 | 54 |
|
|
|
|
| 9 | 4 | 3 | 2 | 1 | 8 | 9 | 10 | 6 | 5 | 7 |
| 14 | 15 | 13 | 12 | 17 | 16 | 11 | 20 | 19 | 18 |
| 26 | 28 | 29 | 30 | 21 | 22 | 23 | 24 | 25 | 27 |
| 32 | 31 | 34 | 35 | 36 | 37 | 38 | 33 | 39 | 40 |
| 47 | 48 | 49 | 50 | 42 | 43 | 44 | 45 | 46 | 41 |
| 53 | 60 | 59 | 52 | 58 | 56 | 55 | 54 | 57 | 51 |
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Задачи с 1 – 10. Найти производные заданных функций:
1.
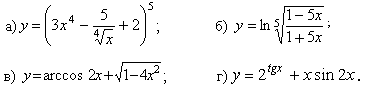
2.
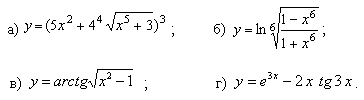
3.
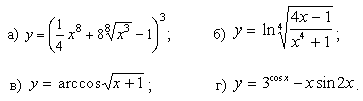
4.
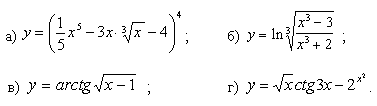
5.
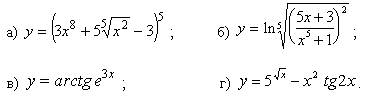
6.
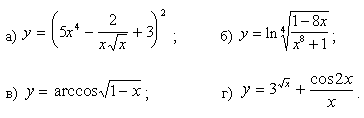
7.
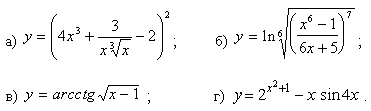
8.
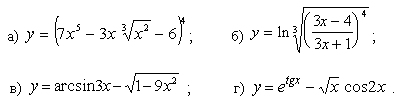
9.
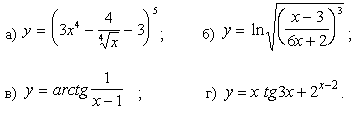
10.
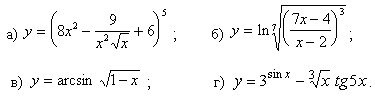
Задачи с 11 – 20. Исследовать средствами дифференциального исчисления функцию y=f(x) и построить ее график.
y = x3 - 9x2 + 24x - 16
y = x3 -11x2 + 39x - 45
y = x3 + 6x2 + 9x + 4
y = x3 + x2 - 5x + 3
y = x3 + 10x2 +32x + 32
y = x3 + 9x2 + 24x + 20
y = x3 - 14x2 + 60x - 72
y = x3 - 12x2 + 45x - 54
y = x3 - 18x2 + 105x -196
y = x3 - 10x2 + 28x - 24
Задачи с 21 – 30. Найти неопределенные интегралы. Результаты проверить дифференцированием.
21.
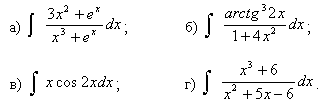
22.
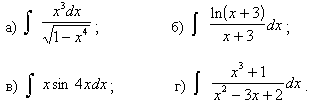
23.
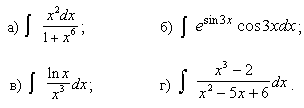
24.
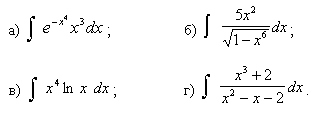
25.
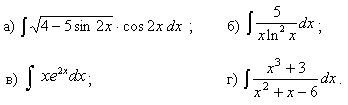
26.
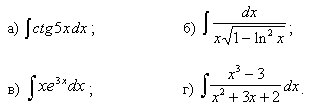
27.
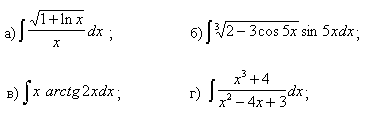
28.
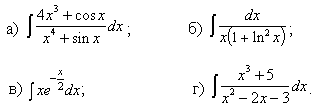
29.
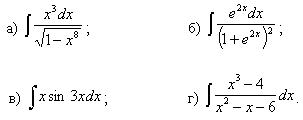
30.
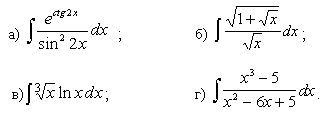
Задачи с 31 – 40. Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж.
у = -х2 + 4х - 1; у = -х - 1.
у = х2 - 6х + 7; у = х + 1
у = -х2 + 6х -5; у = х - 5
у = х2 - 6х + 7; у = -х + 7
у =-х2 + 6х - 5; у = -х + 1
у = х2 + 6х + 7; у = х + 7
у = -х2 - 6х - 5; у = х + 1
у = х2 + 6х + 7; у = -х + 1
у = -х2 - 6х - 6; у = -х - 6
у = х2 - 4х + 1; у = х + 1
Задачи с 41 – 50.Задачи на непосредственное вычисление вероятностей
Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0.06, на втором - 0.02. Производительность первого автомата втрое больше, чем второго. а) Найти вероятность того, что наудачу взятая с конвейера деталь нестандартна. б) Взятая с конвейера деталь оказалась нестандартной. Найти вероятность того, что она изготовлена на первом автомате.
Три хлебокомбината города производят продукцию, обеспечивающую город хлебобулочными продуктами в пропорции 2:3:5. Первый хлебокомбинат производит 30% продукции высшего качества, второй - 40%, третий - 60%. Найти вероятность того, что приобретенное хлебобулочное изделие оказалось высшего качества. Приобретенный продукт оказался высшего качества, найти вероятность того, что это изделие изготовлено на втором хлебокомбинате.
Сообщение можно передать письмом, по телефону и по факсу с одинаковой вероятностью. Вероятность того, что сообщение дойдет до получателя в каждой из перечисленных возможностей соответственно равны 0.7, 0.6 и 0.9. 1) Какова вероятность получения сообщения? 2) Сообщение адресатом получено, какова вероятность, что оно передано по факсу?
В группе 25 студентов: 4 отличника, 9 хорошистов, остальные - троечники. Вероятность получения оценки “отлично” на экзамене по математике для первых - 0.95, для вторых - 0.7, для троечников - 0.3. 1) Какова вероятность того, что наудачу взятый студент получил на экзамене пятерку? 2) Студент получил пятерку на экзамене. Найти вероятность, что он хорошист.
Из 1000 экземпляров однотипного товара 300 принадлежат первой партии, 500 - второй и 200 - третьей. В первой партии 6%, во второй 5%, в третьей 4% бракованного товара. 1) Определить вероятность того, что наудачу выбранный экземпляр бракованный. 2) Наудачу выбранный экземпляр оказался стандартным, найти вероятность того, что он принадлежит третьей партии.
В торговое предприятие поступают однотипные изделия с трех фирм-производителей: 30% с первой, 50% со второй, 20% с третьей. Среди изделий первой фирмы 80% первосортных, второй - 90%, третья фирма изготовляет 70% первосортных изделий. 1) Куплено одно изделие, Найти вероятность того, что оно первосортное. 2) Купленное изделие оказалось не первосортным, найти вероятность того, что оно изготовлено третьей фирмой.
В ящике три детали, причем равновероятны все возможные предположения о числе стандартных деталей. В этот ящик брошена стандартная деталь после чего наудачу извлекается одна деталь. Найти вероятность того, что эта деталь стандартна.
В урне 7 белых и 3 красных шара. Из урны удаляются два шара, о цвете которых неизвестно. После этого из урны извлекается один шар, найти вероятность того, что этот шар красный.
На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0.8, для второго - 0.9. Производительность второго станка втрое больше, чем первого. 1) Найти вероятность того, что взята наудачу деталь стандартна. 2) Взятая наудачу деталь оказалась бракованной, найти вероятность того, что она сделана на первом станке.
В компьютерном классе института 7 IBM типа Pentium и 5 компьютеров других модификаций. Вероятность сбоя в работе в течение учебного занятия для Pentium равна 0.9, для других компьютеров - 0.7. Студент на занятии работает за произвольно выбранным компьютером. 1) Найти вероятность того, что в течение занятия его компьютер не “зависнет”. 2) На занятии компьютер дал сбой в работе, найти вероятность того, что студент работал на Pentiumе.
Задачи с 51 по 60. Дискретные случайные величины
Найти математическое ожидание a) M(X), b) дисперсию D(X), c)среднее квадратическое отклонение  (X) дискретной случайной величины X по заданному закону распределения.
(X) дискретной случайной величины X по заданному закону распределения.
| X | -3 | 0 | 1 | 3 |
| p | 0,1 | 0,2 | 0,4 | 0,3 |
| X | 1 | 3 | 4 | 7 |
| p | 0,1 | 0,5 | 0,2 | 0,2 |
| X | 2 | 3 | 5 | 6 |
| P | 0,3 | 0,2 | 0,1 | 0,4 |
| X | -3 | -2 | 1 | 3 |
| p | 0,1 | 0,5 | 0,2 | 0,2 |
| X | 1 | 2 | 4 | 5 |
| p | 0,4 | 0,3 | 0,1 | 0,2 |
| X | 2 | 5 | 6 | 8 |
| p | 0,1 | 0,6 | 0,1 | 0,2 |
| X | -4 | -2 | 0 | 5 |
| p | 0,4 | 0,2 | 0,1 | 0,3 |
| X | 1 | 3 | 5 | 6 |
| p | 0,5 | 0,1 | 0,1 | 0,3 |
| X | 2 | 3 | 6 | 8 |
| p | 0,1 | 0,4 | 0,3 | 0,2 |
| X | 2 | 5 | 6 | 8 |
| p | 0,1 | 0,4 | 0,1 | 0,2 |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Дифференциальное исчисление и его приложения
Пример1. Вычислить производную функции 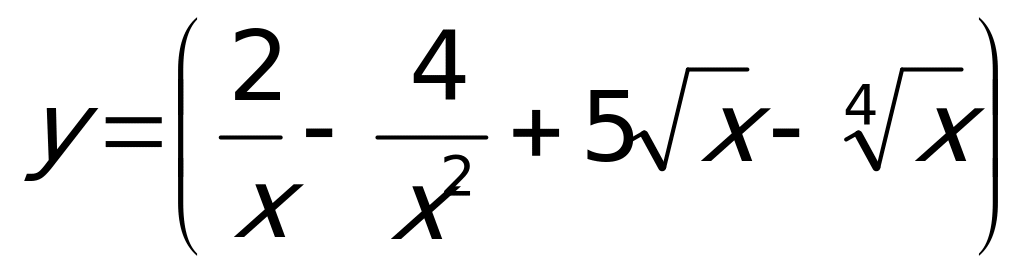 .
.
Производная от суммы (разности) функций равна сумме (разности) производных этих функций. Производную от каждого из слагаемых будем брать как производную от степенной функции: 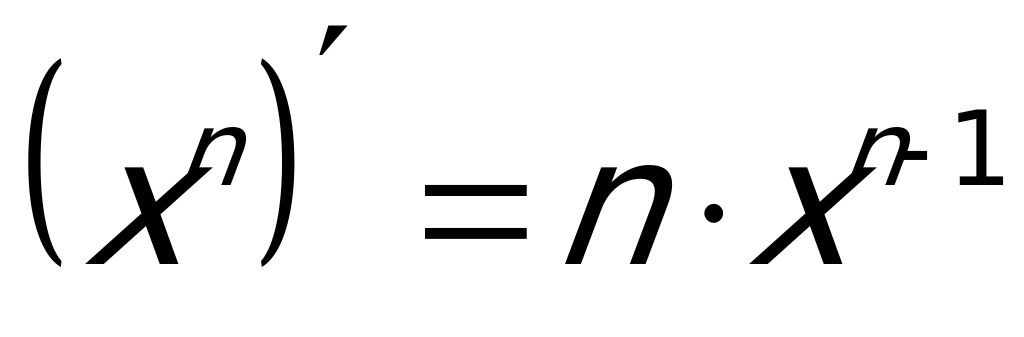 . Учтем, что постоянный множитель выносится за знак производной. Поэтому
. Учтем, что постоянный множитель выносится за знак производной. Поэтому
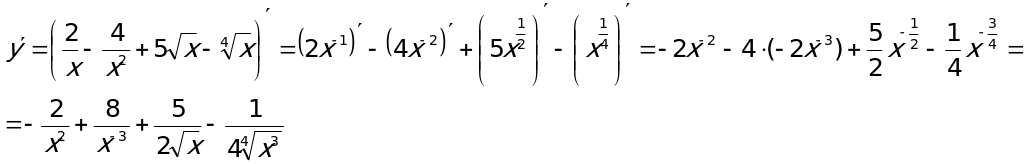 Пример 2. Вычислить производную функции.
Пример 2. Вычислить производную функции. 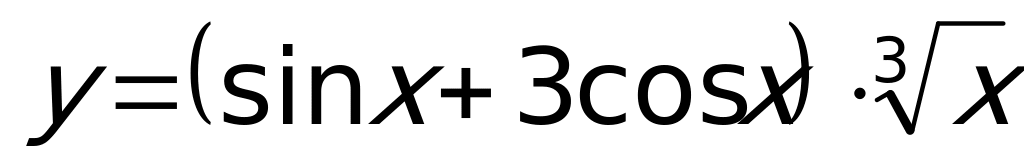 .
.
Применяем формулу для производной от произведения функций: 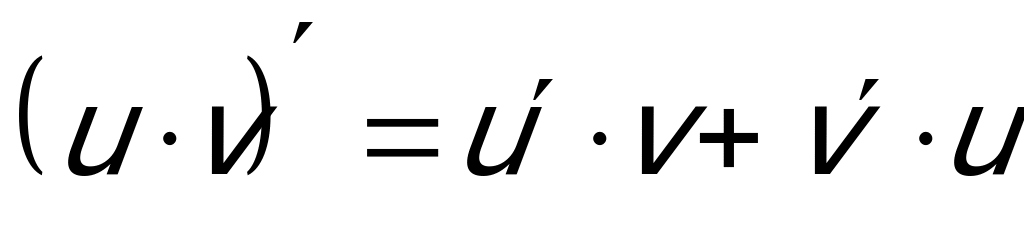 , при этом учитываем, что:
, при этом учитываем, что: 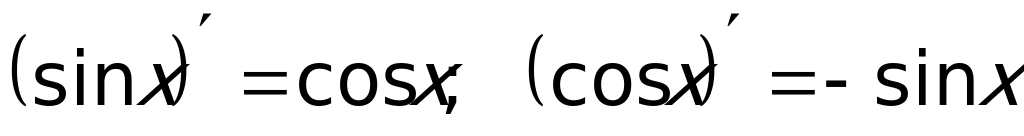 .
.
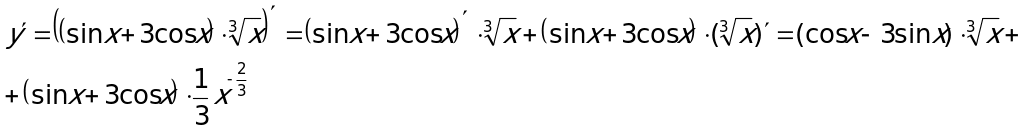 (дальнейшие преобразования в этих примерах можно не проводить).
(дальнейшие преобразования в этих примерах можно не проводить).
Пример 3. Вычислить производную функции. 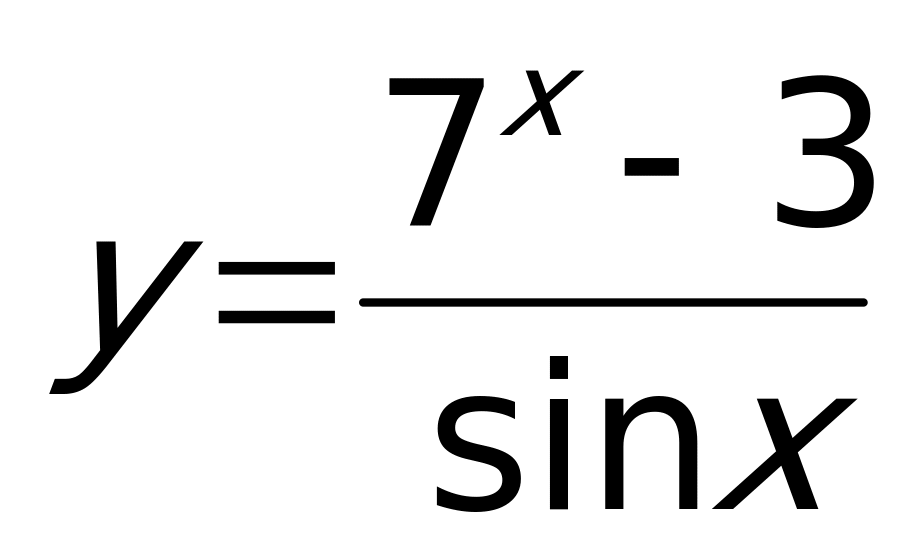 .
.
Применяем формулу производной частного двух функций: 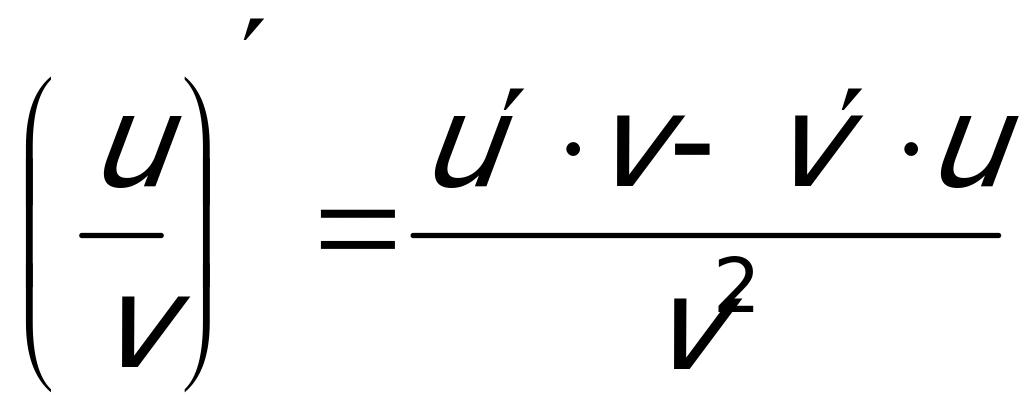 . Учитываем, что производная показательной функции
. Учитываем, что производная показательной функции 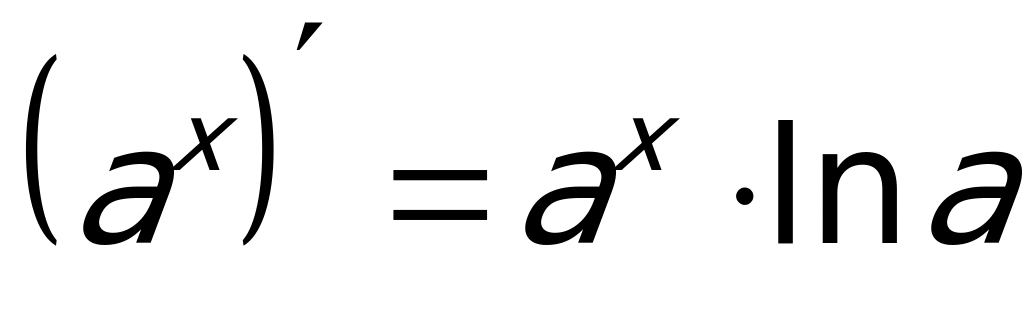 :
:
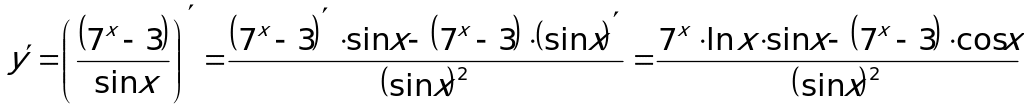 .
.
Пример 4. Вычислить производную функции 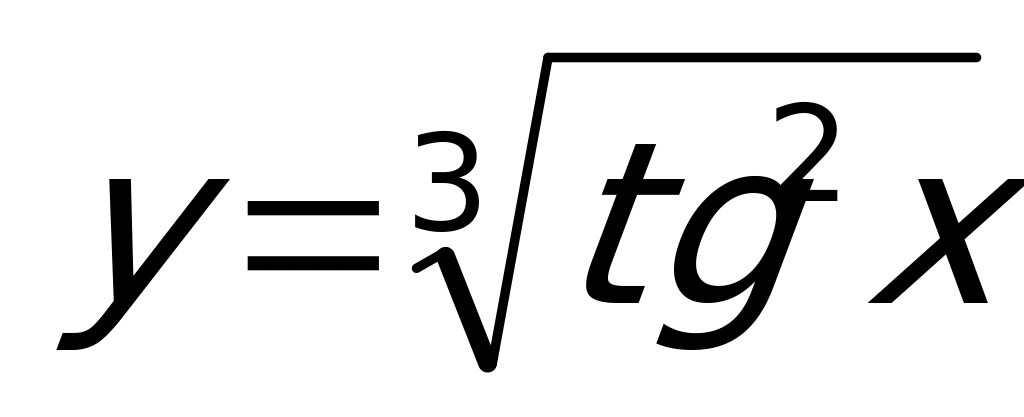 .
.
Производная от сложной функции находится по правилу: если 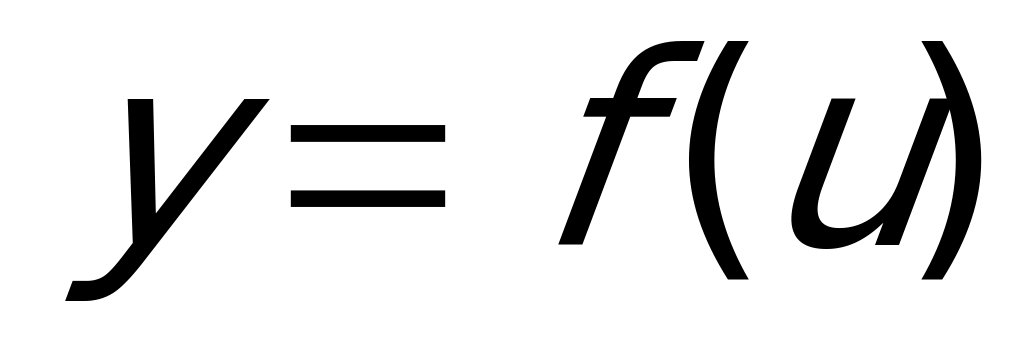 и
и 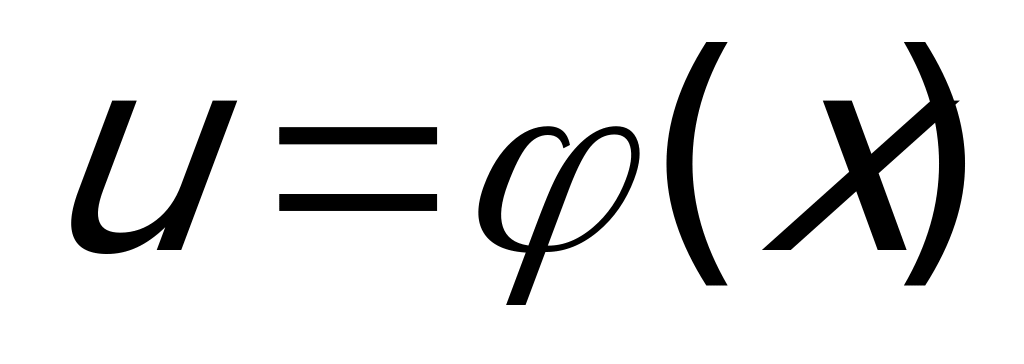 - непрерывные функции, то производная сложной функции
- непрерывные функции, то производная сложной функции 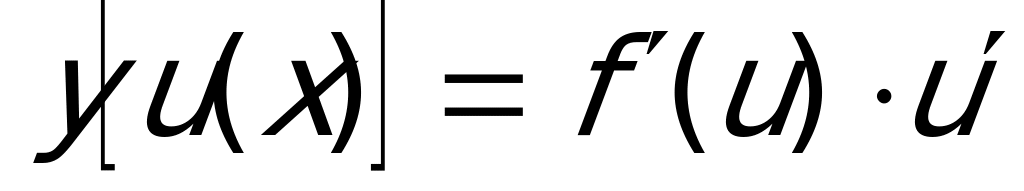 . Т.е. она вычисляется как произведение производной данной функции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной. В нашем случае можно заданную функцию представить как
. Т.е. она вычисляется как произведение производной данной функции по промежуточному аргументу и производной самого промежуточного аргумента по независимой переменной. В нашем случае можно заданную функцию представить как 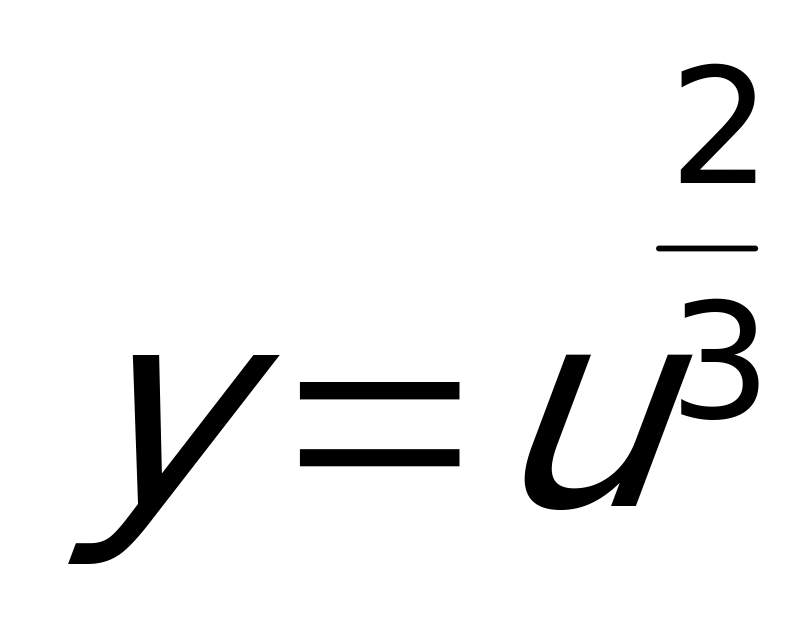 , где
, где 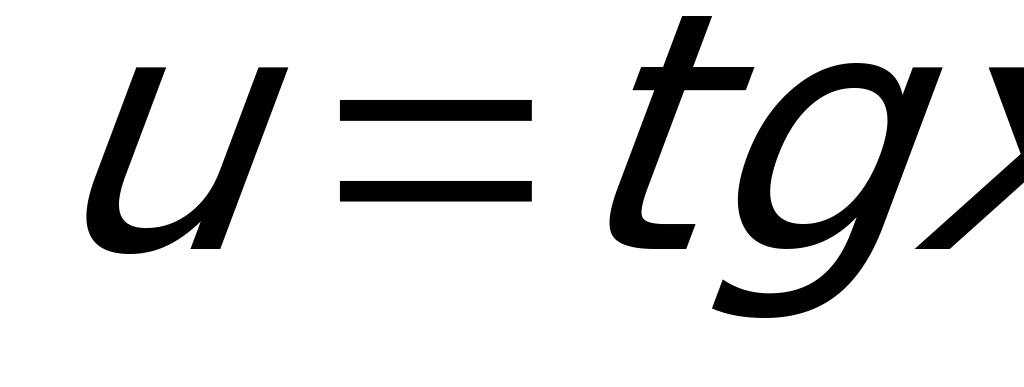 . Тогда на основании этого правила сначала берем производную от степенной функции, а затем от тангенса:
. Тогда на основании этого правила сначала берем производную от степенной функции, а затем от тангенса:
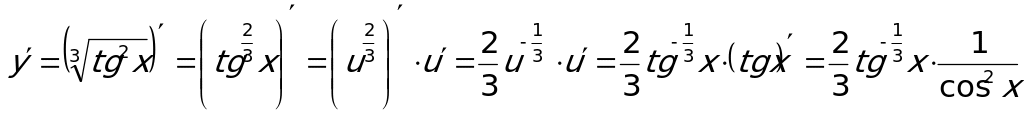 .
.
(Здесь учли также, что 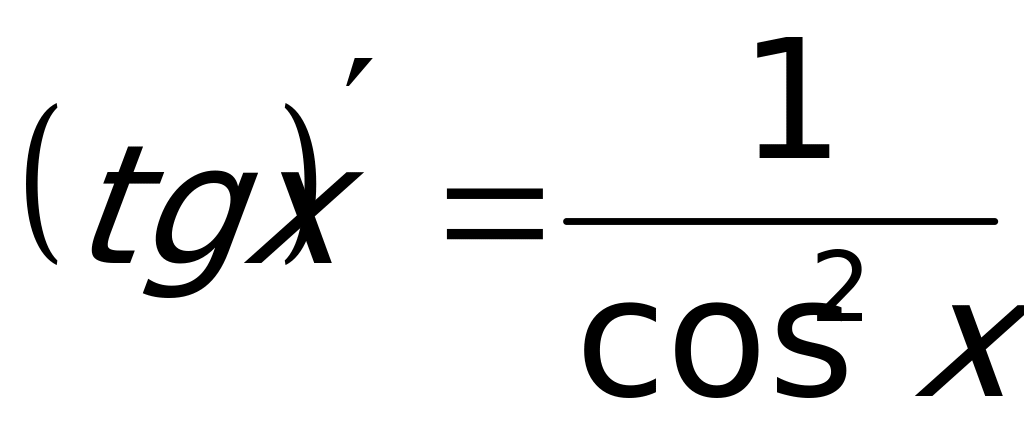 ).
).
Пример 5. Вычислить производную функции: 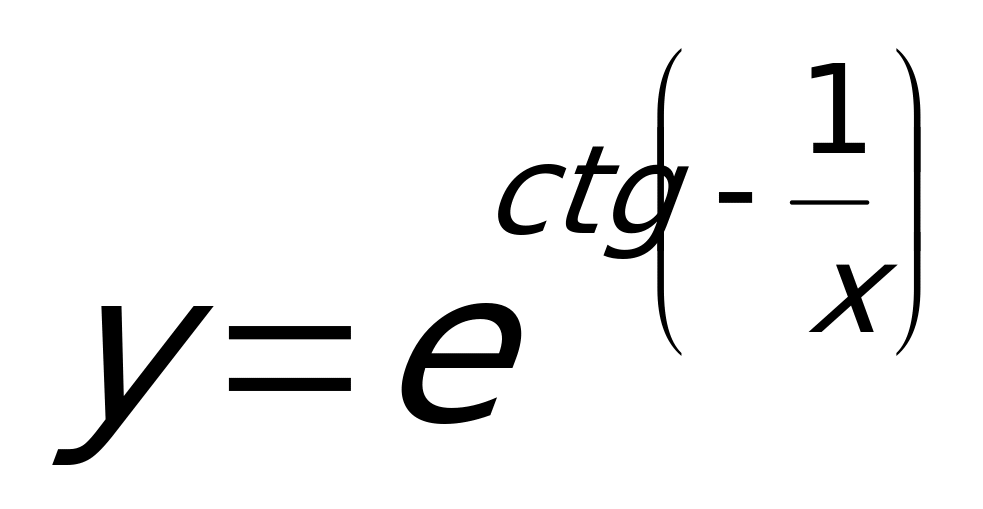 .
.
В данном случае также имеем сложную функцию, которую можно представить так: 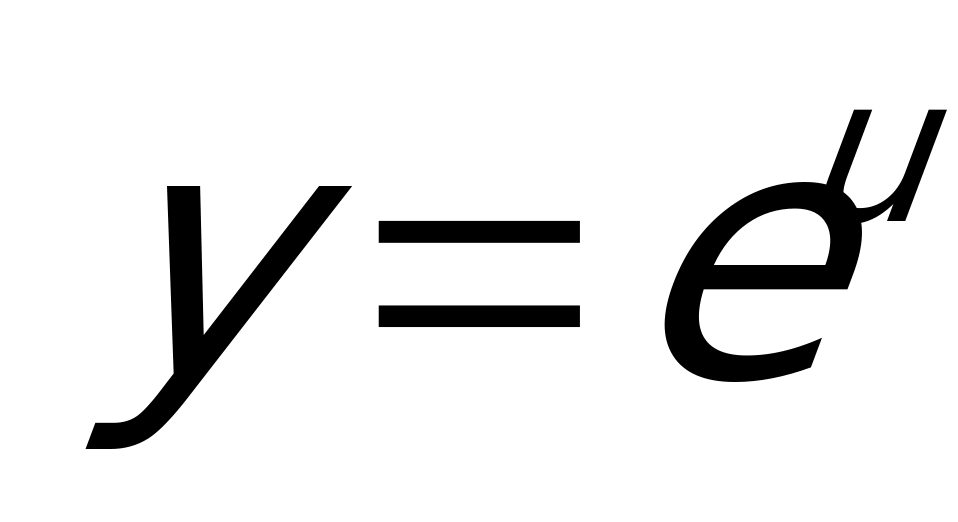 , где
, где 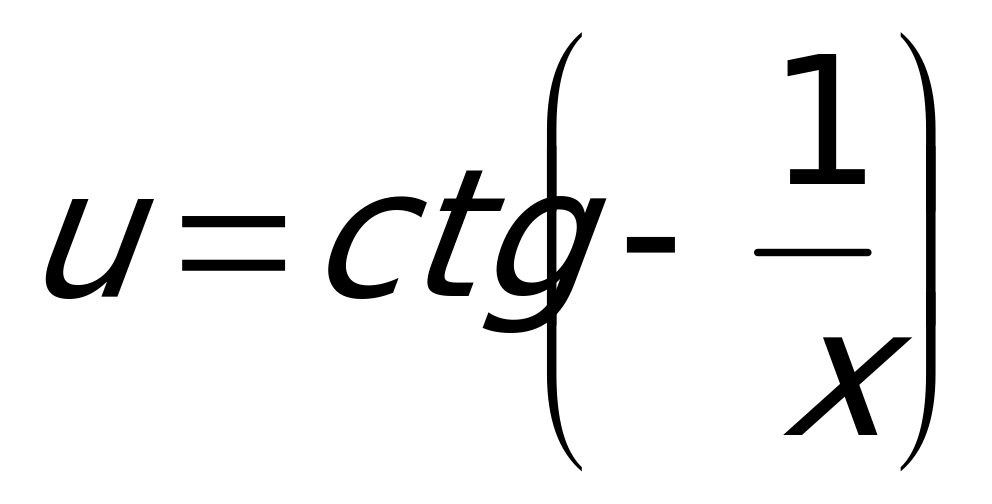 - тоже является сложной функцией:
- тоже является сложной функцией: 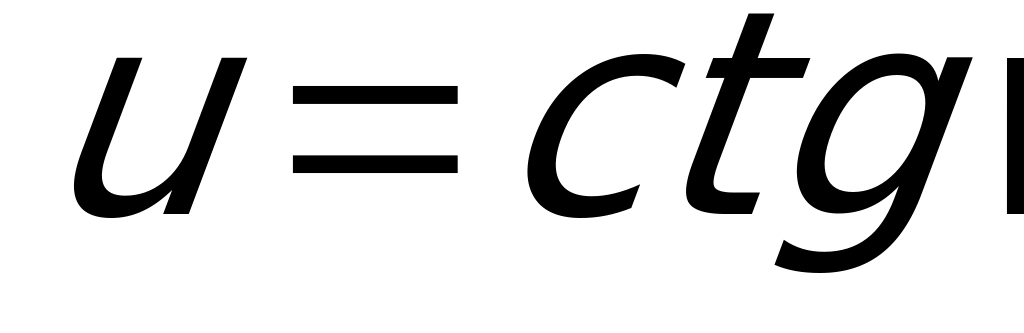 и
и 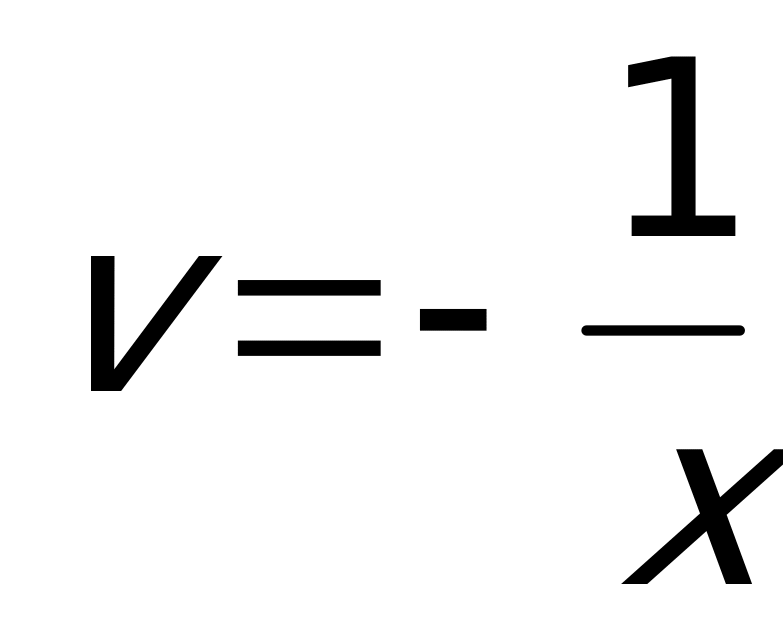 . Поэтому сначала берем производную от экспоненциальной функции, затем от котангенса, и, наконец, от
. Поэтому сначала берем производную от экспоненциальной функции, затем от котангенса, и, наконец, от 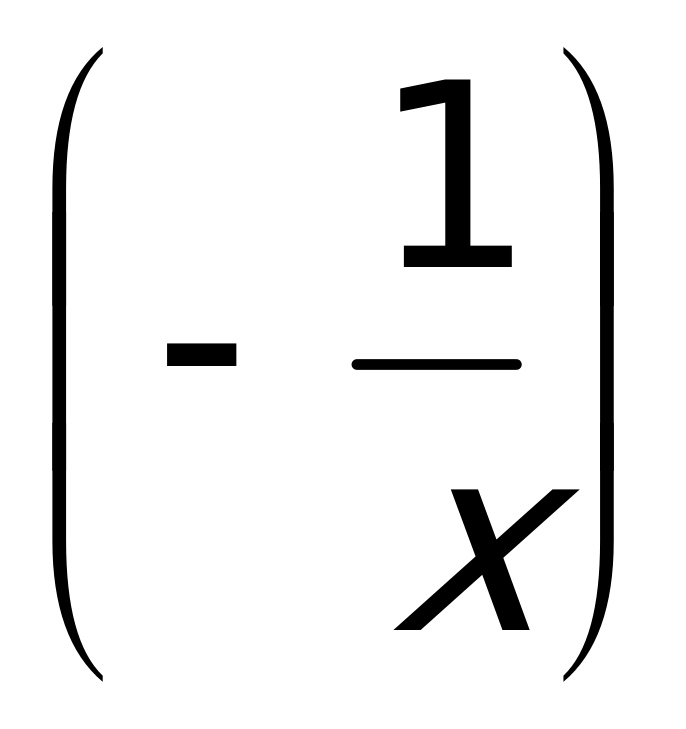 и результаты этого дифференцирования перемножаем:
и результаты этого дифференцирования перемножаем:
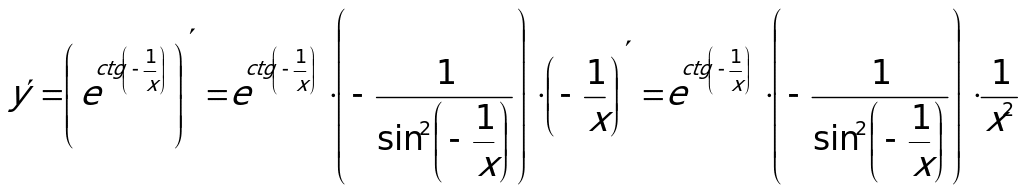
Пример 6. Вычислить производную функции 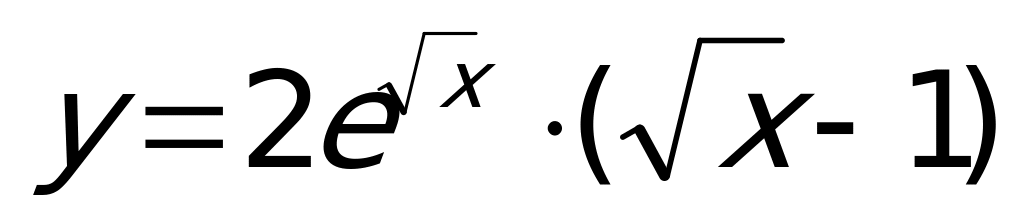 .
.
Будем искать производную этой функции, как производную произведения, причем первый сомножитель представляет собой сложную функцию 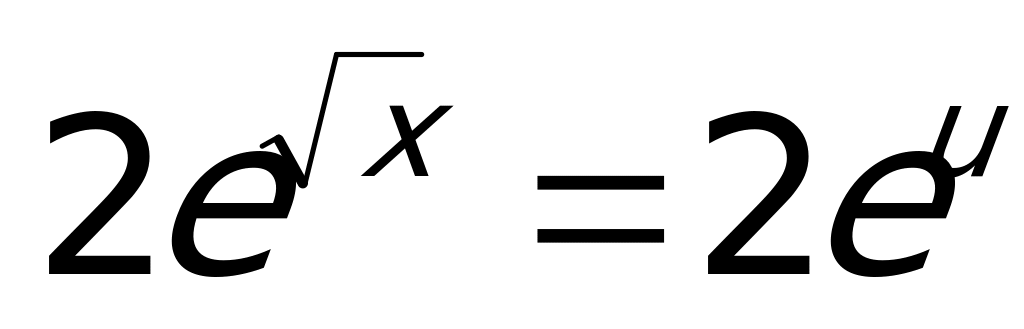 , где
, где 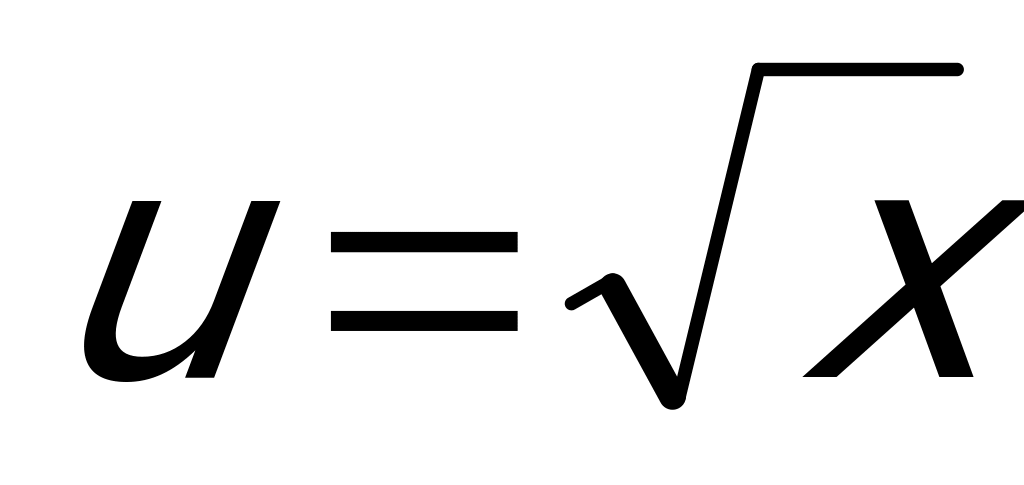 :
:
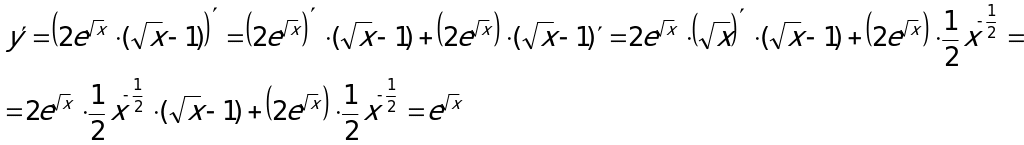 Пример 7. Вычислить производную функции
Пример 7. Вычислить производную функции 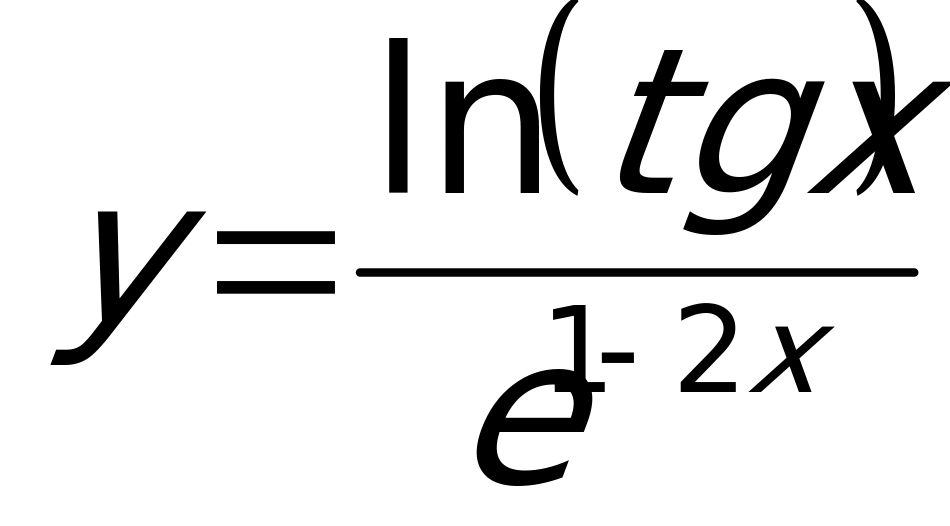 .
.
Используем формулу производной частного двух функций, учтем, что и числитель и знаменатель являются сложными функциями:
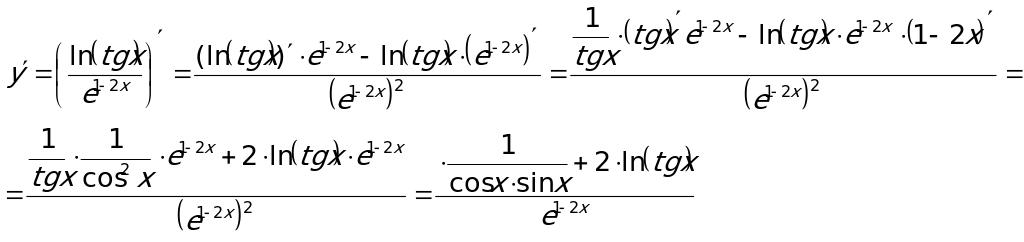
Интегральное исчисление
Интегрирование есть операция, обратная дифференцированию. 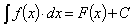 , где F(x)-первообразная для подынтегральной функции f(x), то есть F`(x)=f(x), а С – произвольная постоянная. При интегрировании часто используют свойства неопределенного интеграла:
, где F(x)-первообразная для подынтегральной функции f(x), то есть F`(x)=f(x), а С – произвольная постоянная. При интегрировании часто используют свойства неопределенного интеграла:
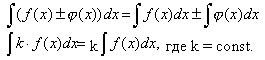
Идея интегрирования заключается в том, чтобы свести данный интеграл к одному из табличных интегралов. Поэтому, приступая к решению задач ознакомьтесь с таблицей интегралов.
Примечание. Формулы верны, когда х является независимой переменной, а также когда х является функцией другой переменной: х=х(t).
Интегралы а) и б) в ваших контрольных работах берутся методом замены переменной (подстановкой).
При этом вводится новая переменная t=(x) , которая является функцией от x. Если новая переменная введена удачно, то в результате замены получаем табличные интегралы.
Некоторые рекомендации по введению новой переменной смотрите ниже в примерах.
Напомним формулу для нахождения дифференциала функции одной переменной:

Пример 1.
Если под знаком интеграла содержится показательная функция, то за новую переменную t часто удобно принимать показатель степени, если к тому же под интегралом присутствует производная этого показателя с точностью до постоянного множителя.
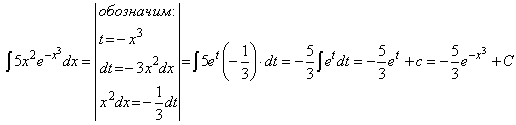
В конце возвращаемся к старой переменной, подставив вместо t выражение (-x3).
Проверка: Если интеграл взят правильно, то производная от полученного результата равна подынтегральной функции:
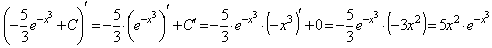 ,
,
что и требовалось доказать.
Пример 2.
Если под интегралом содержится логарифмическая функция, то часто удобно принять ее за новую переменную, если под знаком интеграла присутствует к тому же и производная этой функции (с точностью до постоянного множителя).
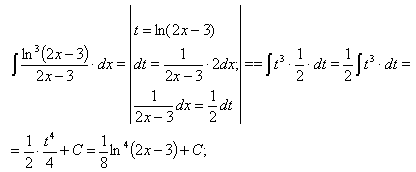
Проверка:
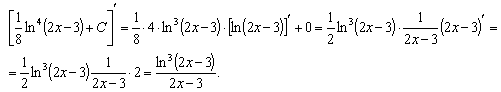
Пример 3.
Часто удобно обозначать за новую переменную знаменатель дроби подынтегральной функции.
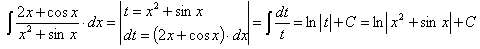
Проверка:
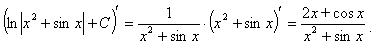
Пример 4.
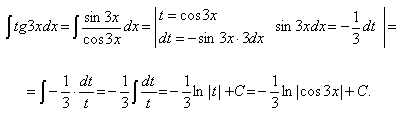
Проверка:
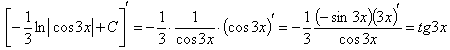
Пример 5.
Часто за новую переменную удобно взять подкоренное выражение, если под интегралом присутствует также его производная с точностью до постоянного множителя.
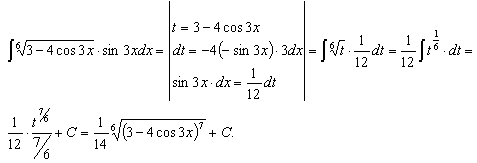
Проверка:
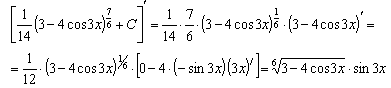
Пример 6.
Подстановка выбирается аналогично предыдущему примеру.
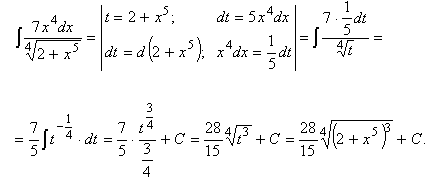
Пример 7.
Новая переменная иногда выбирается из следующих соображений: в знаменателе стоит разность постоянной и квадрата некоторой функции. Эту функцию мы принимаем за новую переменную, если в числителе присутствует ее производная (с точностью до постоянного множителя).
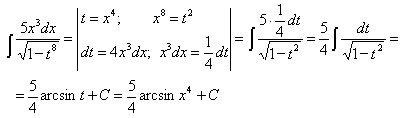
Пример 8.
Подстановка выбирается аналогично предыдущему примеру.
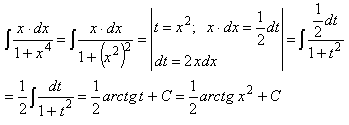
Пример 9.
За новую переменную иногда выбирают функцию, стоящую в основании степени, если подынтегральное выражение содержит производную этой функции с точностью до постоянного множителя.
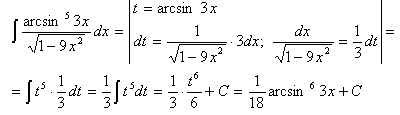
Пример 10.
Подстановка выбирается аналогично предыдущему примеру.
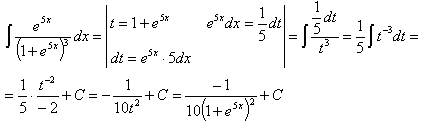
Сделайте самостоятельно проверку в примерах 6-10.
Интеграл из пункта в) вашей контрольной работы берется методом интегрирования “по частям”. Этим методом интегрируются некоторые произведения, например произведения степенной функции на логарифмическую или на показательную, или на тригонометрическую, или на обратные тригонометрические функции и др.
Интегрирование “по частям” производится по формуле
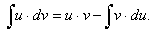
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за “u”, а оставшийся множитель вместе с dx принять за “dv”.
Для того, чтобы интеграл в правой части был проще данного интеграла, надо правильно выбрать “u” и “dv”.
В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за “u”. Если подынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за “u” принимается степенная функция.
Пример 11.
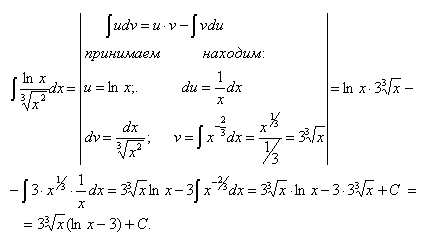
Пример 12.
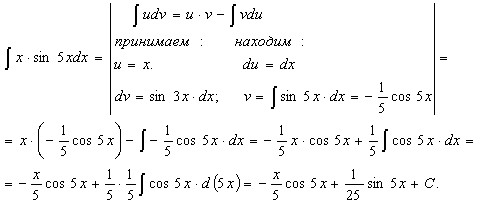
Пример 13.
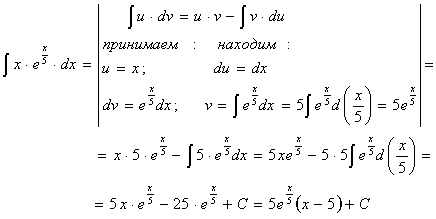
Пример 14.
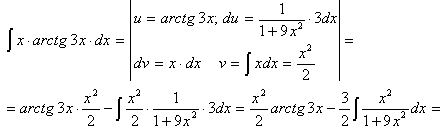
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем в числителе прибавим и отнимем единицу, после чего разобьем интеграл на два табличных:
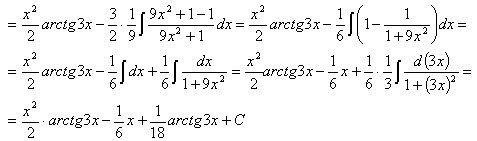
Обязательно сделайте проверку в примерах 11-14.
В пункте г) вашей контрольной работы предлагается взять интеграл от рациональной дроби.
Пример 15.
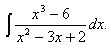
Под знаком интеграла стоит рациональная дробь.
Так как подинтегральная рациональная дробь неправильная (степень многочлена в числителе выше степени многочлена в знаменателе),то выделим целую часть, разделив числитель на знаменатель “углом” (аналогично тому, как в задачах 41-50):
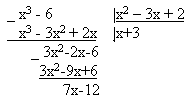
Итак, подынтегральную функцию можно записать в виде:
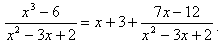
Тогда данный интеграл (обозначим его J), можно представить как сумму интегралов:
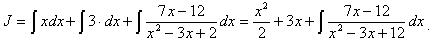
Чтобы взять полученный новый интеграл от правильной рациональной дроби (обозначим его J1, разложим знаменатель подынтегральной функции на множители.
Для этого найдем корни квадратного трехчлена, стоящего в знаменателе: x2-3x+12=0.
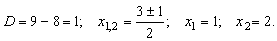
Тогда
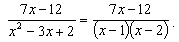
Представим полученную правильную дробь в виде суммы элементарных дробей:
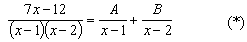
Здесь А и В - числа, которые нужно найти. Сделаем приведение к общему знаменателю в правой части:
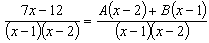
Так как дроби тождественно равны и равны их знаменатели, то должны быть равны и их числители:
7x-12=A(x-2)+B(x-1);
7x-12=Ax-2A+Bx-B;
7x-12=(A+B)x+(-2A-B).
Это тождество выполняется тогда и только тогда, когда слева и справа равны коэффициенты при одинаковых степенях х:
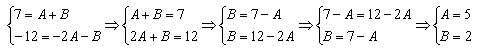
Получена система двух уравнений с двумя неизвестными А и В, решив которую, найдем А=5; В=2.
Подставим найденные числа в равенство (*):
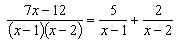
Вернемся к интегралу J1:
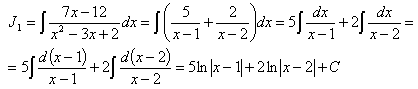
Окончательно искомый интеграл равен:
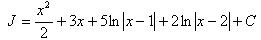
Проверка:
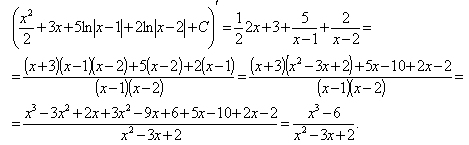
В задачах используется определенный интеграл, который вычисляется по формуле Ньютона-Лейбница.
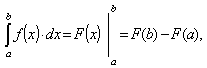
где F(х) – первообразная для 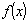 , то есть
, то есть 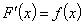 ;
;
a и b - пределы интегрирования, показывающие, как меняется переменная интегрирования х.
Обратите внимание на то, что определенный интеграл – это число, в отличие от неопределенного интеграла, который является множеством функций. Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл (вернее, найти лишь одну первообразную, не прибавляя произвольной постоянной), а затем вычислить разность значений первообразной в верхнем и нижнем пределах.
Задача.
Вычислить площадь фигуры, ограниченной параболой у=x2-6x+5 и прямой y = x-1. Сделать чертеж.
Решение.
Построим параболу и прямую.
Для построения параболы найдем координаты ее вершины и точки пересечения ее с осями координат.
Вершина параболы является точкой экстремума, поэтому для ее отыскания найдем производную и приравняем ее к нулю.
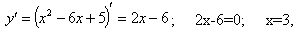
тогда 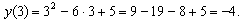
Итак, вершина параболы в точке (3;-4).
Точки пересечения параболы с осью Ох: y=0, тогда
х2-6х+5=0, откуда х1=1; х2=5, то есть точки (1;0) и (5;0).
Точка пересечения с осью Оу: х=0, тогда y=5; то есть точка (0;5).
Строим параболу по найденным точкам, замечая, что ветви параболы направлены вверх (рис. 9).
Прямую y=х-1 строим по двум точкам: (0;-1) и (1;0).
Получены точки заштрихуем плоскую фигуру, ограниченную параболой и прямой.
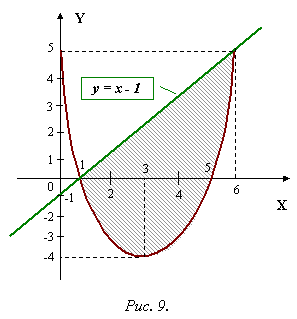
Найдем точки пересечения параболы и прямой, решив систему уравнений:
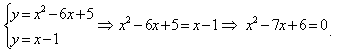
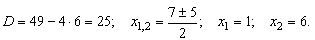
Для отыскания искомой площади воспользуемся формулой
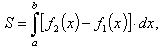
где функции 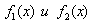 ограничивают фигуру соответственно снизу и сверху, то есть
ограничивают фигуру соответственно снизу и сверху, то есть 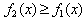 при
при 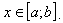
В нашей задаче 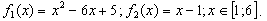
Поэтому:
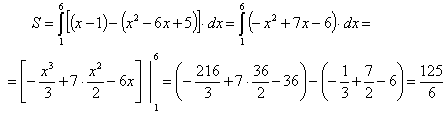
Ответ:
Площадь искомой криволинейной трапеции:
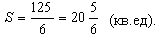
Основные задачи теории вероятностей и математической статистики
Задача 1.Из ящика, в котором содержится 5 белых и 7 красных шаров, вынимают наугад три шара без возвращения. Какова вероятность, что среди вынутых шаров будет 2 белых и один красный?
Решение
| 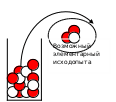 | Опыт: вытаскивание трех шаров из ящика, содержащего 12 шаров. Множество элементарных исходов опыта  - все расстановки из 12 элементов по 3 элемента. - все расстановки из 12 элементов по 3 элемента. Отвечая на вопросы схемы на рис., приходим к выводу, что данные расстановки являются сочетаниями без повторений из 12 по 2, поскольку они отличаются друг от друга составом элементов (шаров), порядок расположения шаров в выборке не важен, элементы не повторяются. |
Следовательно, число всех элементарных исходов опыта:
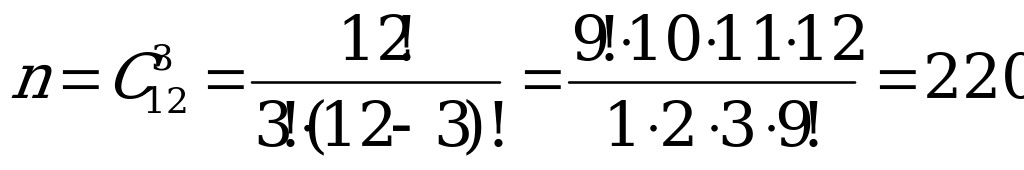 .
.
Событие  : «среди трех вынутых шаров 2 белых и 1 красный».
: «среди трех вынутых шаров 2 белых и 1 красный».
Найдем 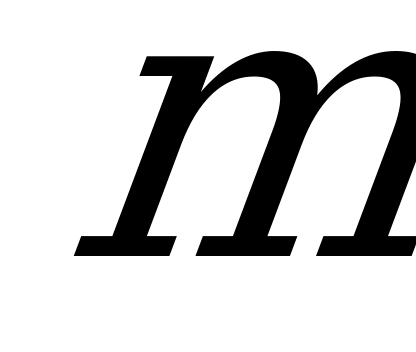 – число элементарных исходов, благоприятствующих событию
– число элементарных исходов, благоприятствующих событию  , т.е. число таких наборов по 3 шара, в которых два шара белые и один – красный.
, т.е. число таких наборов по 3 шара, в которых два шара белые и один – красный.
В ящике 5 белых шаров, а в наборе их должно быть два. Можно составить 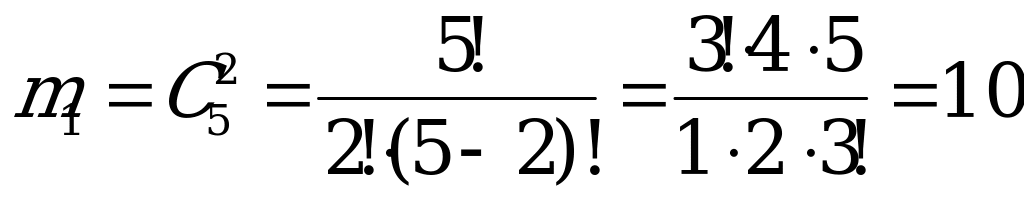 таких выборок. К каждой из 10 выборок можно добавить один из 7 имеющихся красных шаров:
таких выборок. К каждой из 10 выборок можно добавить один из 7 имеющихся красных шаров: 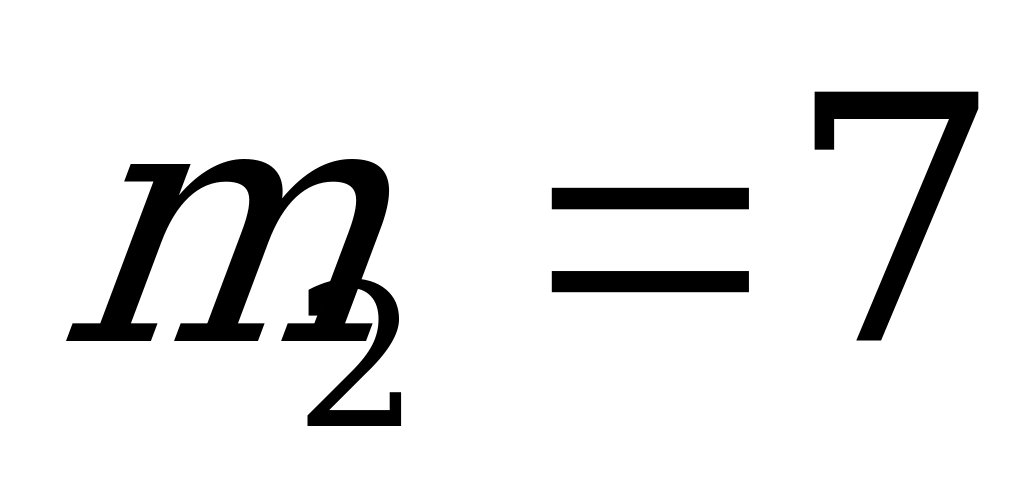 .
.
Пользуясь комбинаторным правилом умножения, получаем:
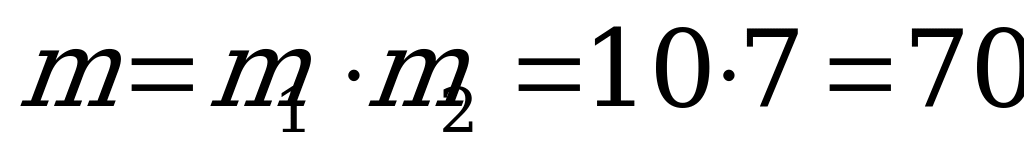 наборов по 3 шара содержат 2 белых и 1 красный шар.
наборов по 3 шара содержат 2 белых и 1 красный шар.
Итак, 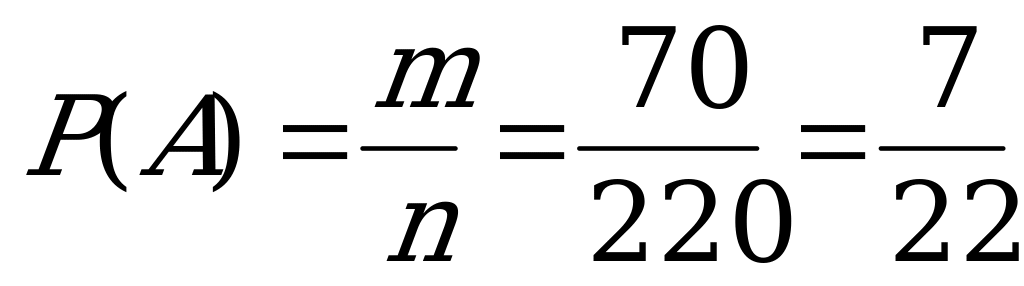 .
.
Задача 2.В первом ряду аудитории 6 парт. За эти парты всегда садятся 6 друзей-студентов. Какова вероятность того, что при случайной посадке за эти парты Саша и Марина окажутся рядом?
Решение
| 1 | 2 | 3 | 4 | 5 | 6 | | А | Б | С | М | К | Д | | А | Б | К | М | Д | С |
| Опыт: рассадить шесть студентов {А,Б,С,М,К,Д} по шести партам {1,2,3,4,5,6}. (Саша и Марина – это М и С). Два возможных элементарных исхода опыта показаны в таблице. |
Множество элементарных исходов опыта  – все расстановки из 6 элементов по 6 элементов. Отвечая на вопросы схемы на рис., приходим к выводу, что данные расстановки являются перестановками из 6 элементов без повторений, поскольку они не отличаются друг от друга составом элементов и элементы не повторяются.
– все расстановки из 6 элементов по 6 элементов. Отвечая на вопросы схемы на рис., приходим к выводу, что данные расстановки являются перестановками из 6 элементов без повторений, поскольку они не отличаются друг от друга составом элементов и элементы не повторяются.
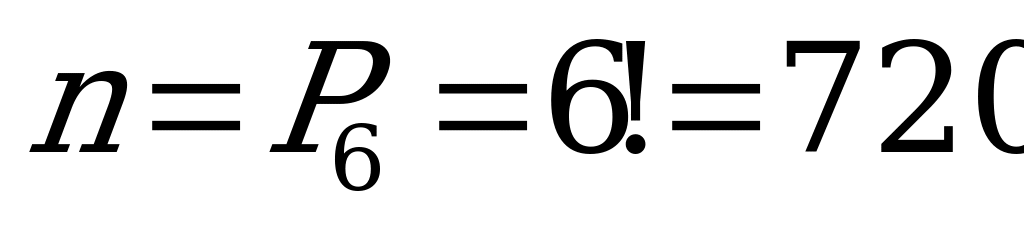 .
.
Событие  : «Саша и Марина сидят рядом».
: «Саша и Марина сидят рядом».
Пусть 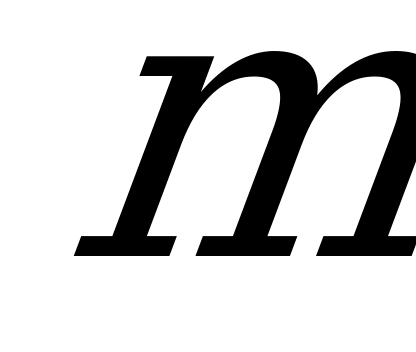 – число элементарных исходов, благоприятствующих событию
– число элементарных исходов, благоприятствующих событию  , т.е. число таких расстановок шести студентов по шести местам, в которых С и М занимают соседние места. Это условие уменьшает число мест в ряду на единицу, т.к. если, например, С занял какое-то место, то оказывается занятым и соседнее место, потому что туда садится М.
, т.е. число таких расстановок шести студентов по шести местам, в которых С и М занимают соседние места. Это условие уменьшает число мест в ряду на единицу, т.к. если, например, С занял какое-то место, то оказывается занятым и соседнее место, потому что туда садится М.
Таким образом, число исходов, благоприятствующих событию  – это число перестановок без повторений из пяти:
– это число перестановок без повторений из пяти:
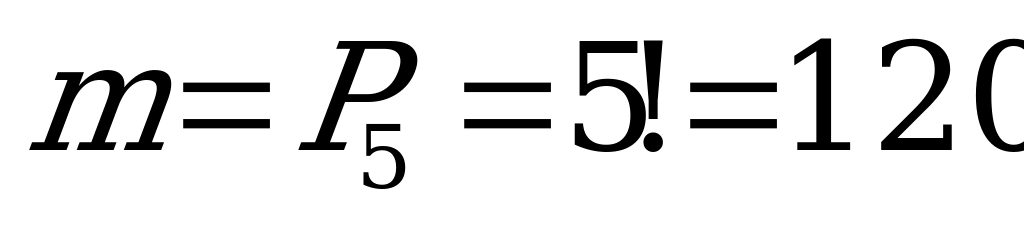 .
.
Итак, 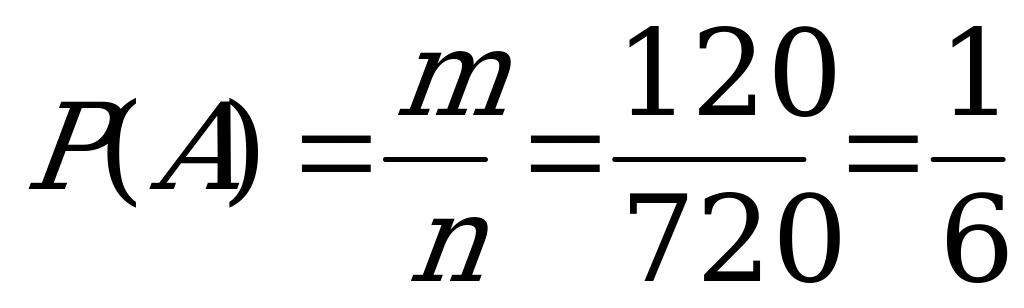 .
.
Задача 3.Три стрелка стреляют по мишени по одному разу. Вероятность попадания в мишень первым стрелком равна 0.7, вторым – 0.8, третьим – 0.9. Найти вероятность того, что мишень будет поражена (а) одной пулей, (б) двумя пулями, (в) хотя бы одной пулей.
Решение
Опыт: Три стрелка сделали по одному выстрелу по мишени. События и их вероятности:
 – попадание первого стрелка,
– попадание первого стрелка, 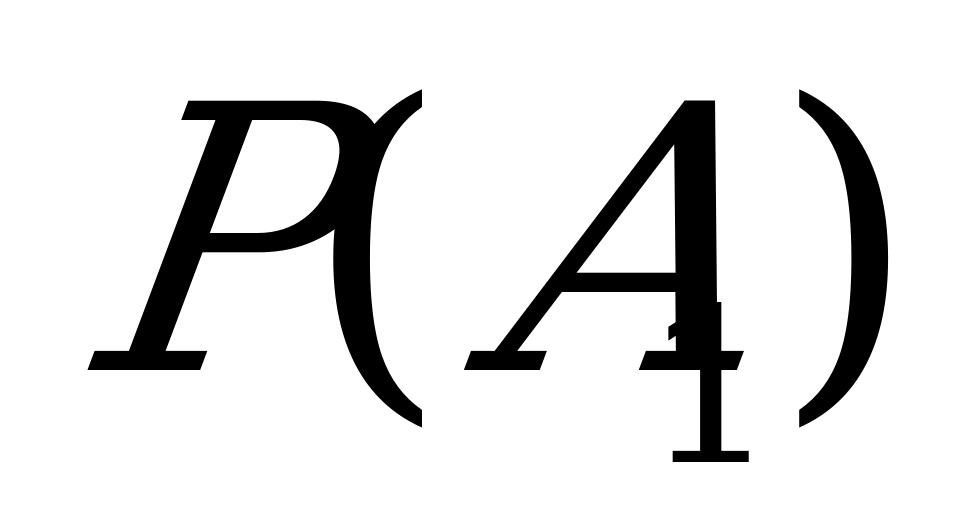 =0.7,
=0.7,  – промах первого стрелка,
– промах первого стрелка,
 =1-
=1-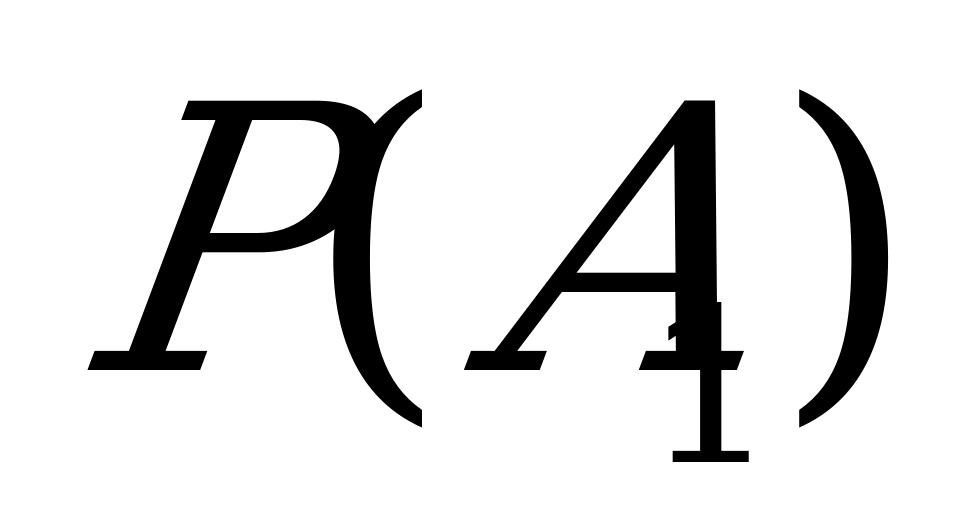 =0.3;
=0.3;
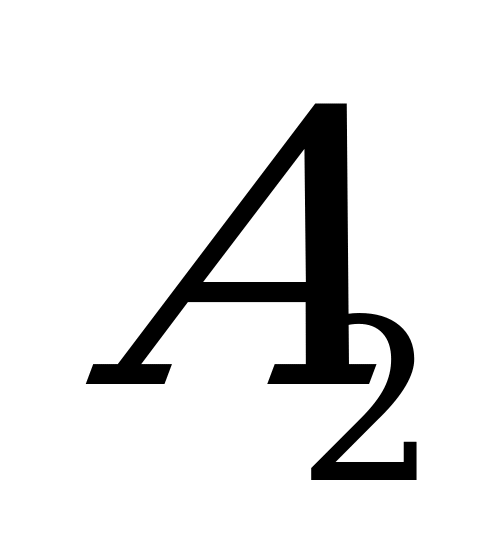 – попадание второго стрелка,
– попадание второго стрелка, 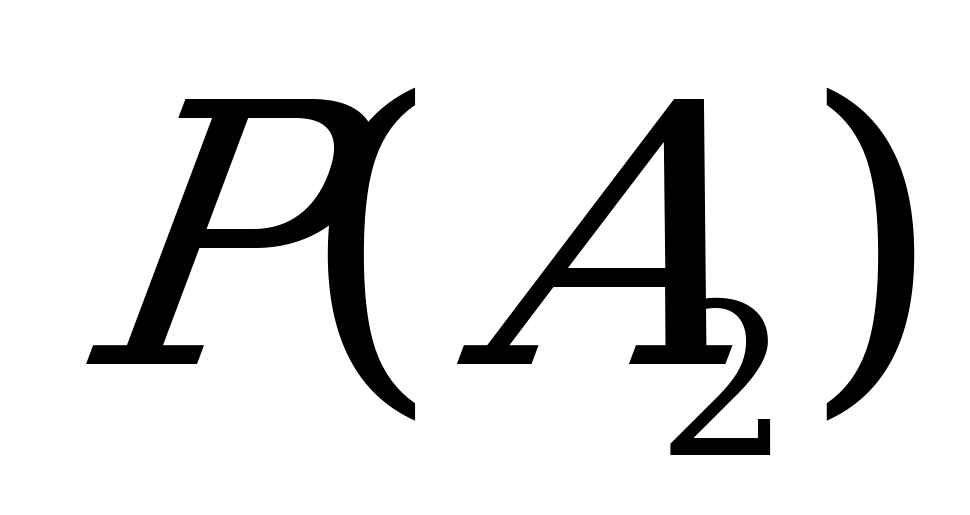 =0.8,
=0.8,  – промах второго стрелка,
– промах второго стрелка,
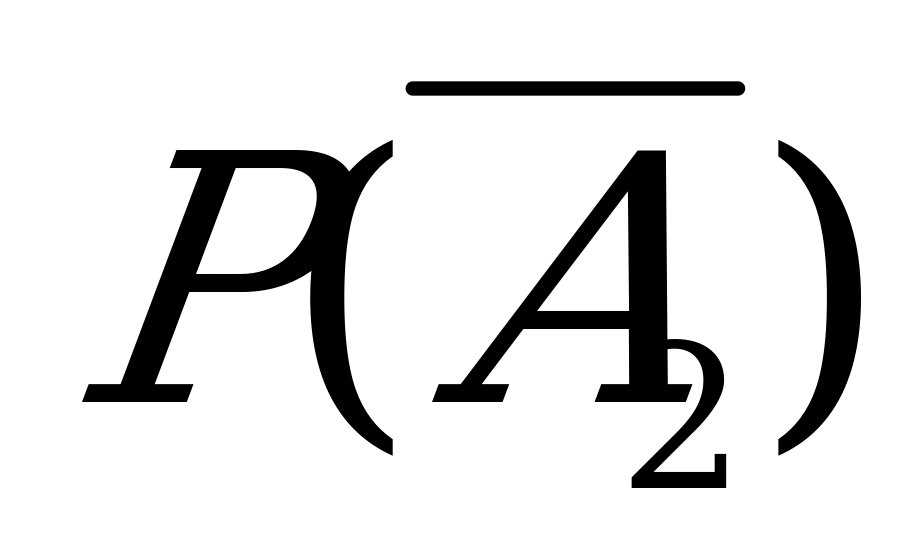 =0.2;
=0.2;
 – попадание третьего стрелка,
– попадание третьего стрелка, 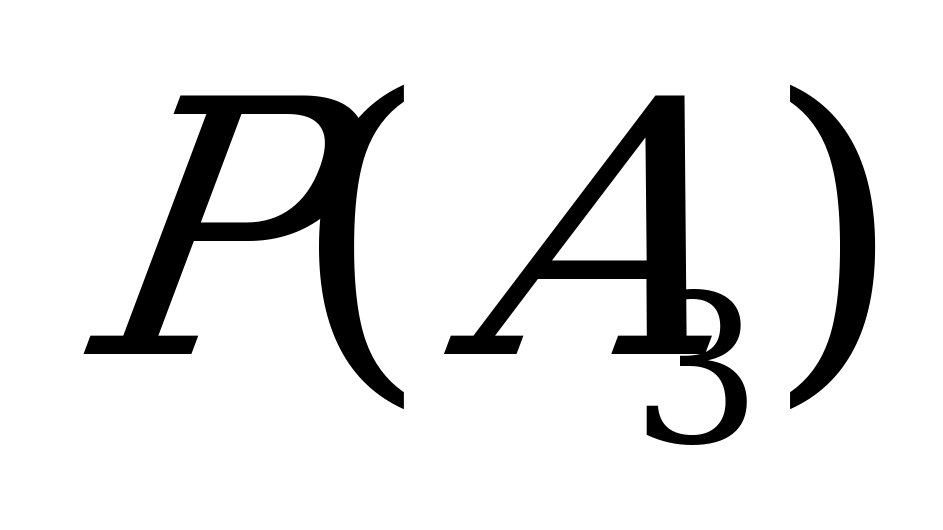 =0.9,
=0.9,  – промах третьего стрелка,
– промах третьего стрелка,
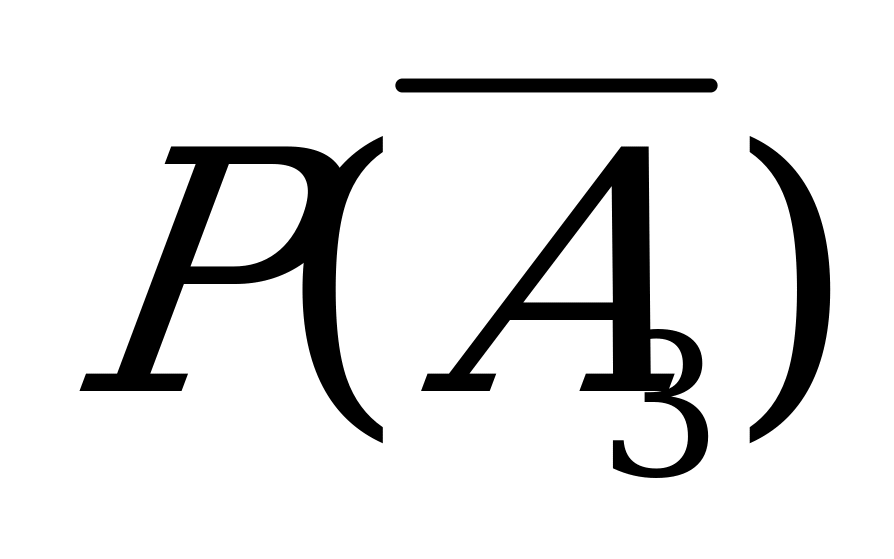 =0.1.
=0.1.
 – один стрелок попал в цель И два промахнулись
– один стрелок попал в цель И два промахнулись
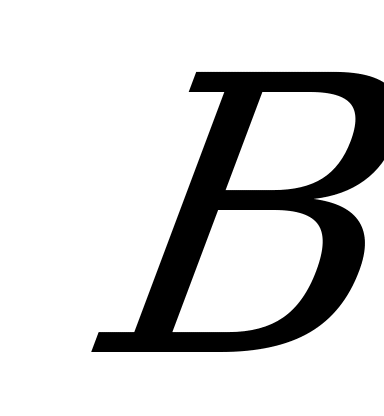 – два стрелка попали в цель И один промахнулся
– два стрелка попали в цель И один промахнулся
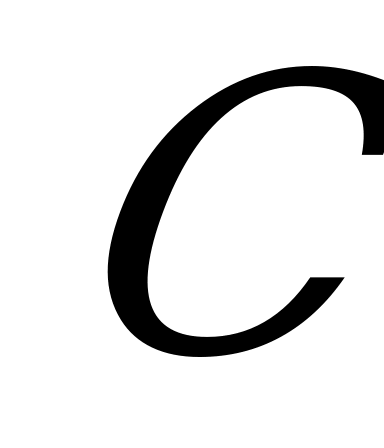 – в цель попал один стрелок ИЛИ два стрелка ИЛИ три стрелка.
– в цель попал один стрелок ИЛИ два стрелка ИЛИ три стрелка.
Найдем вероятность события  . Для этого распишем смысл события
. Для этого распишем смысл события  более подробно:
более подробно:
 – (один стрелок попал в цель И два промахнулись)=(первый стрелок попал И второй промахнулся И третий промахнулся) ИЛИ (первый стрелок промахнулся И второй попал И третий промахнулся) ИЛИ (первый стрелок промахнулся И второй промахнулся И третий попал).
– (один стрелок попал в цель И два промахнулись)=(первый стрелок попал И второй промахнулся И третий промахнулся) ИЛИ (первый стрелок промахнулся И второй попал И третий промахнулся) ИЛИ (первый стрелок промахнулся И второй промахнулся И третий попал).
Заменяя текст символом события, а связки И / ИЛИ – знаками умножения и сложения, получим:
 =
= ·
· ·
· +
+ ·
·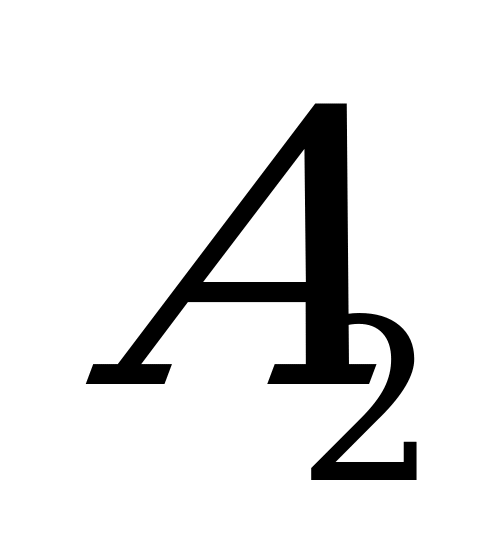 ·
· +
+ ·
· ·
· .
.
События  ·
· ·
· ,
,  ·
·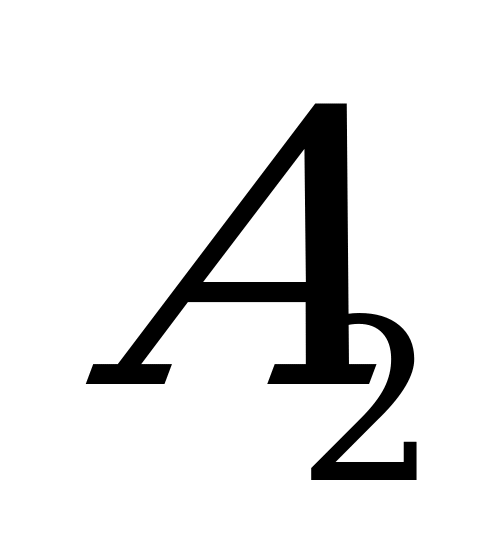 ·
· ,
,  ·
· ·
· несовместны, а события, входящие в произведения – независимы.
несовместны, а события, входящие в произведения – независимы.
Пользуясь теоремами умножения для независимых событий и сложения для несовместных событий, получаем:
 =
=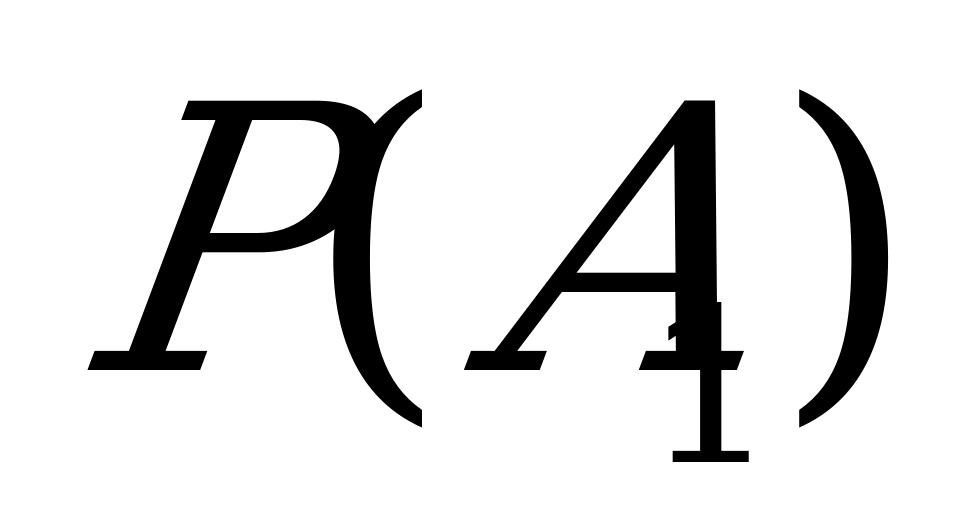 ·
·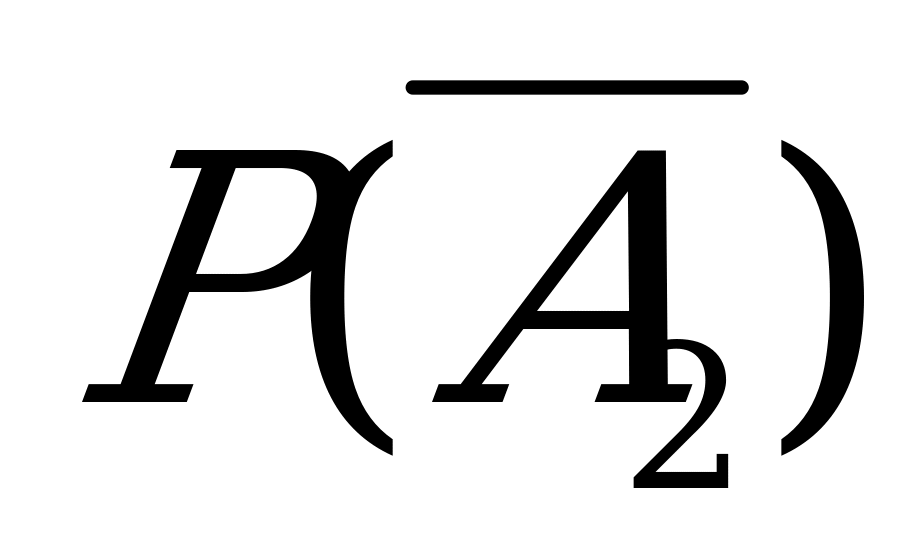 ·
·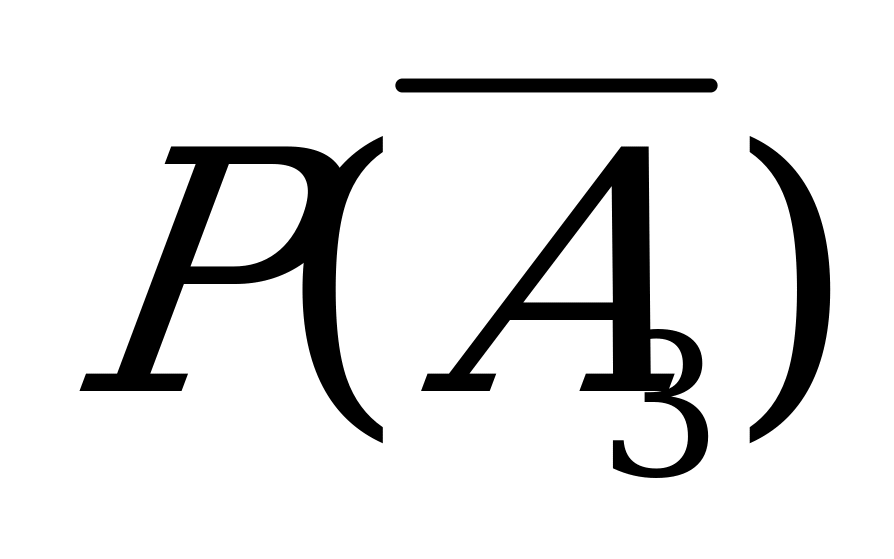 +
+ ·
·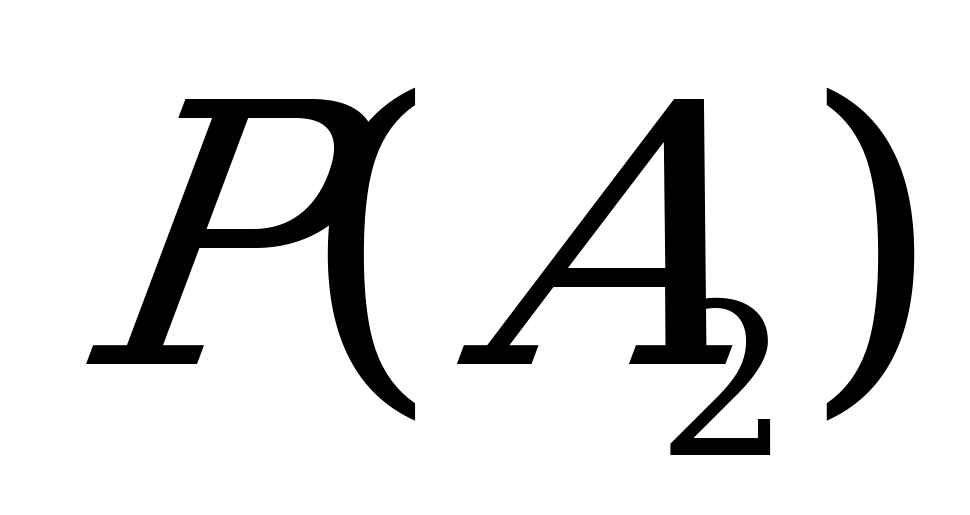 ·
·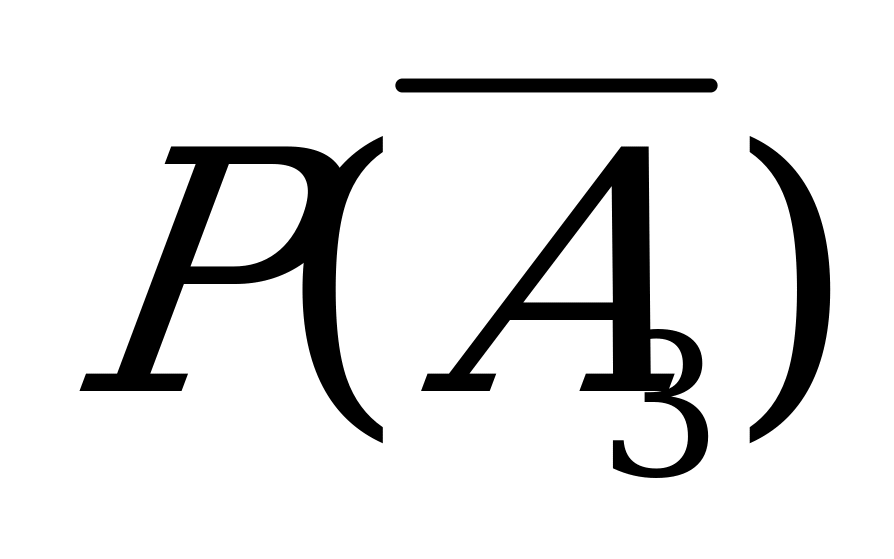 +
+ ·
·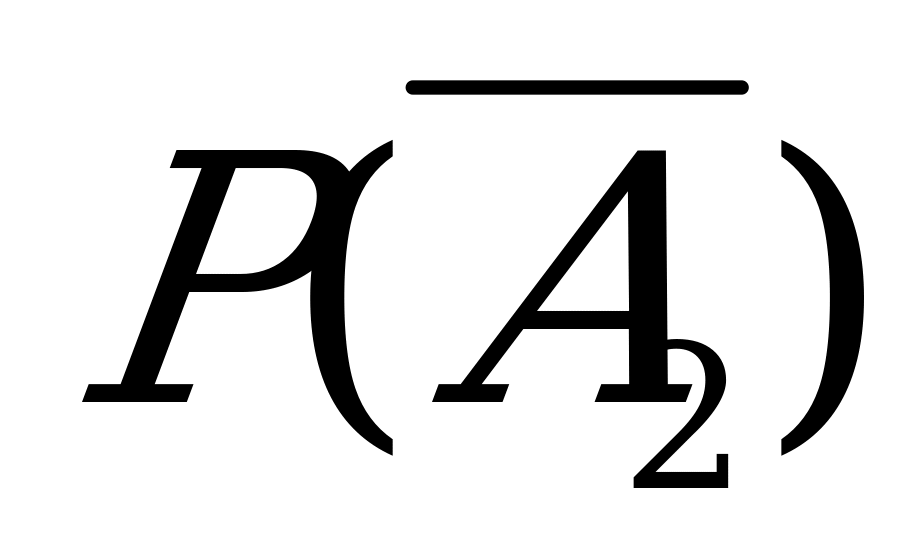 ·
·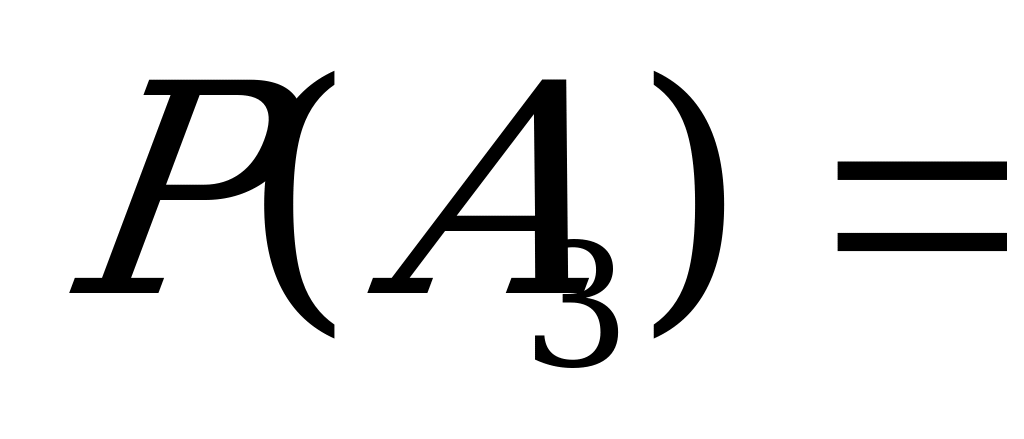
=0.7·0.2·0.1+0.3·0.8·0.1+0.3·0.2·0.9=0.014+0.024+0.056=0.096.
Вероятность поражения цели одной пулей равна 0.096.
Рассуждая аналогично в случае события 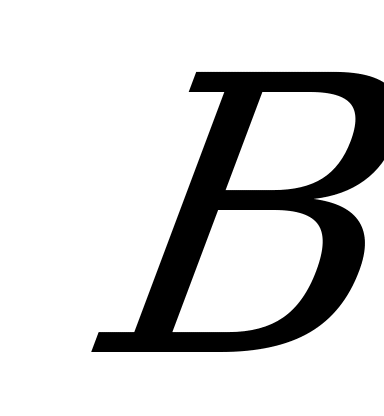 , имеем:
, имеем:
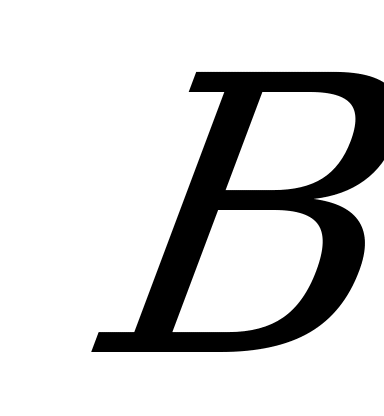 =
= ·
·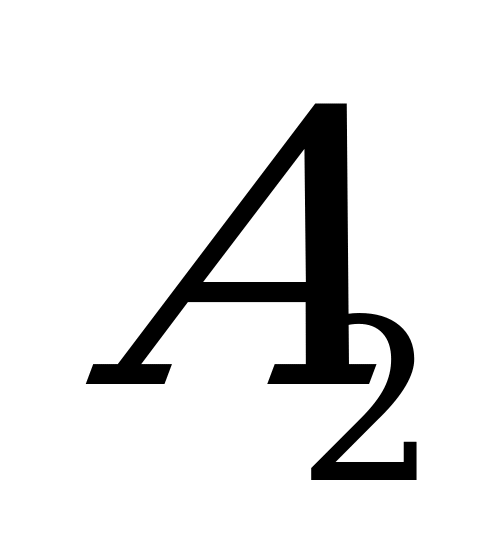 ·
· +
+ ·
· ·
· +
+ ·
·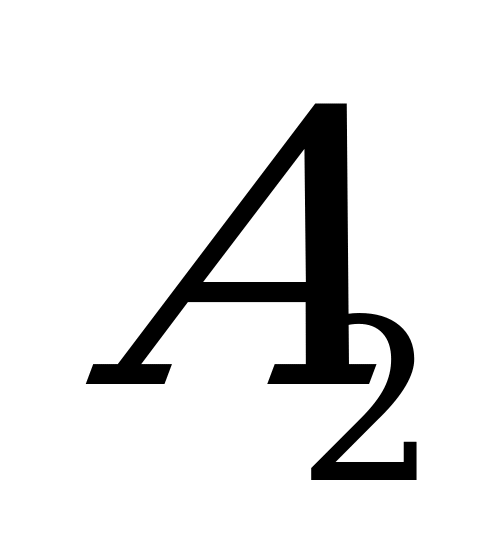 ·
· .
.
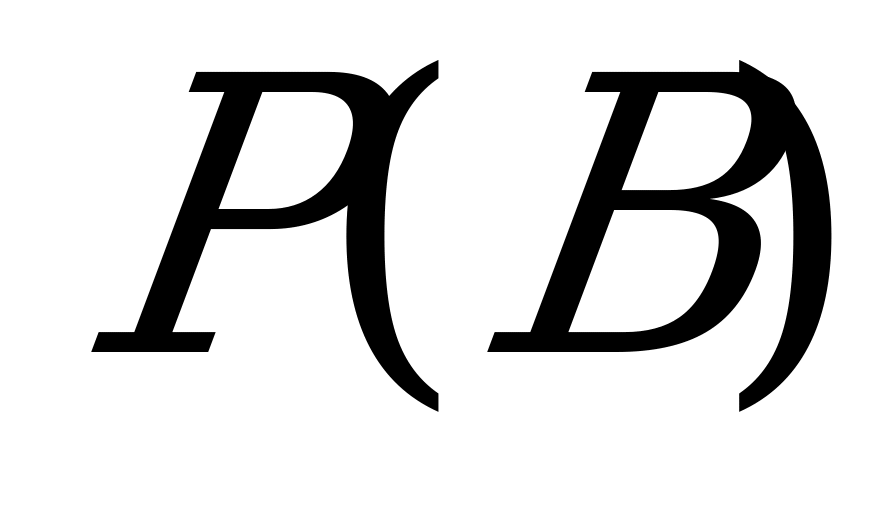 =
=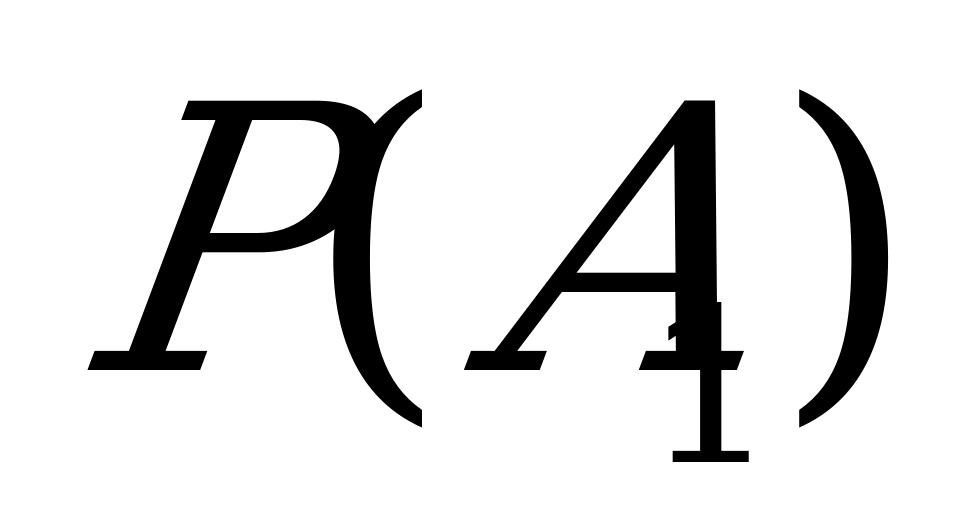 ·
·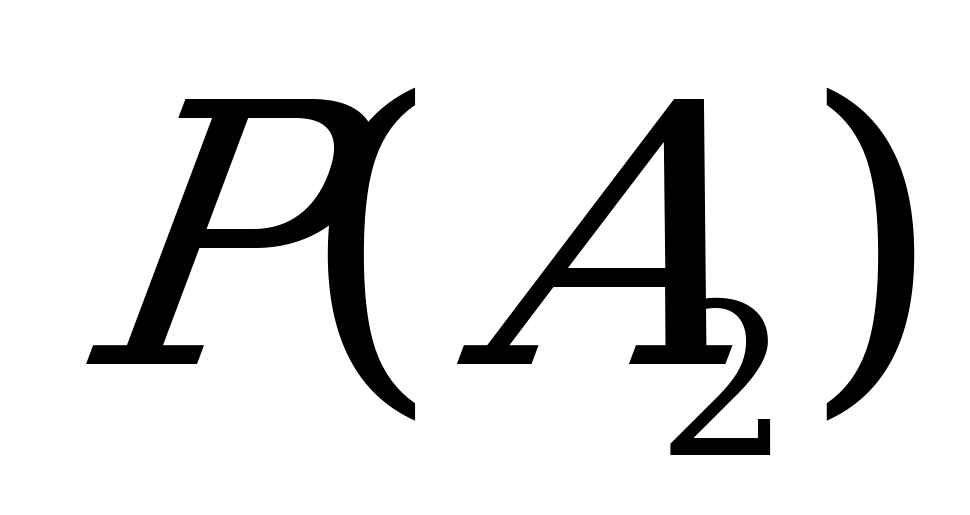 ·
·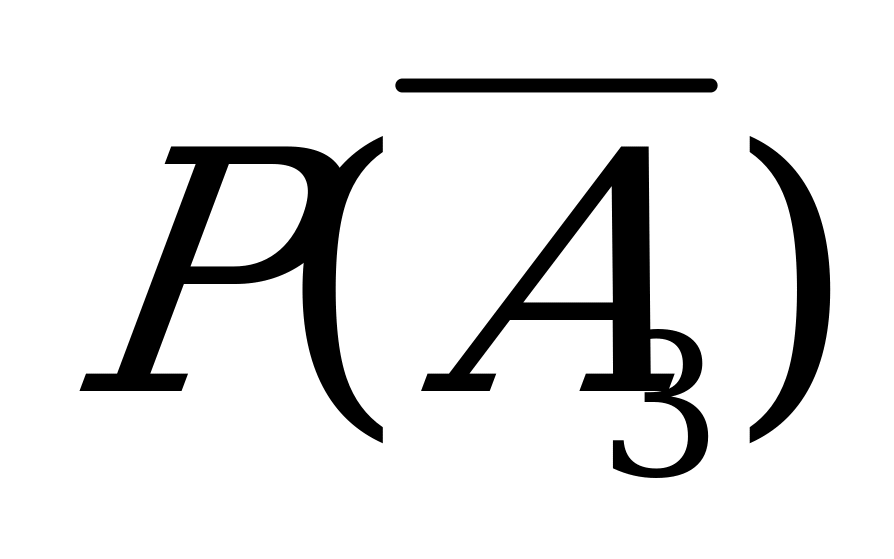 +
+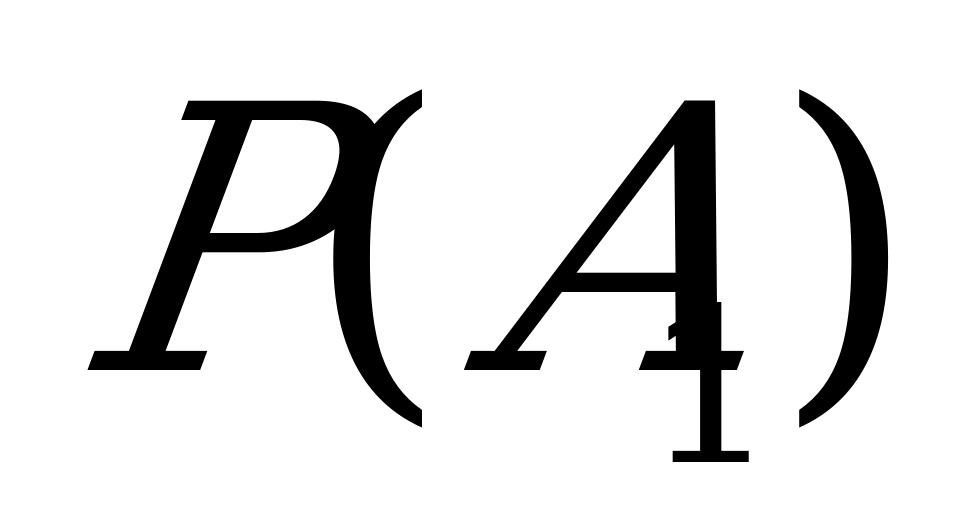 ·
·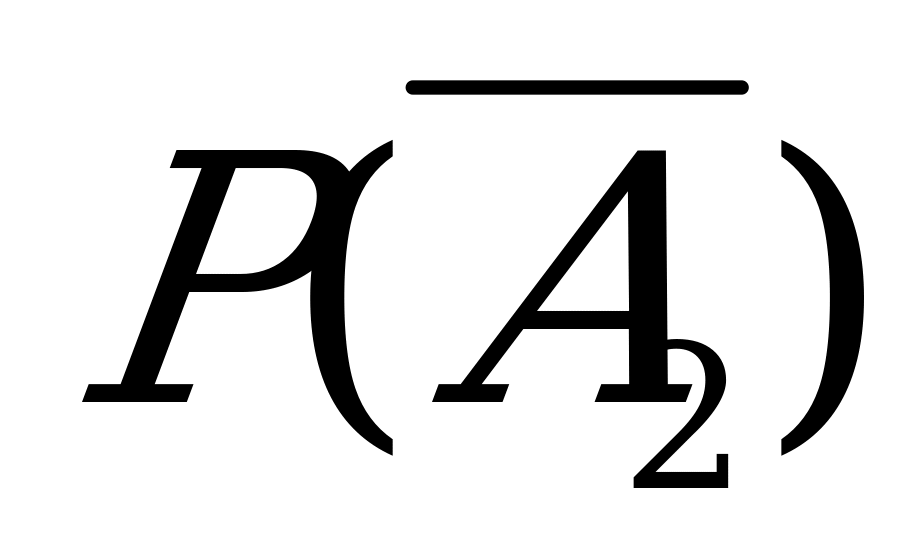 ·
·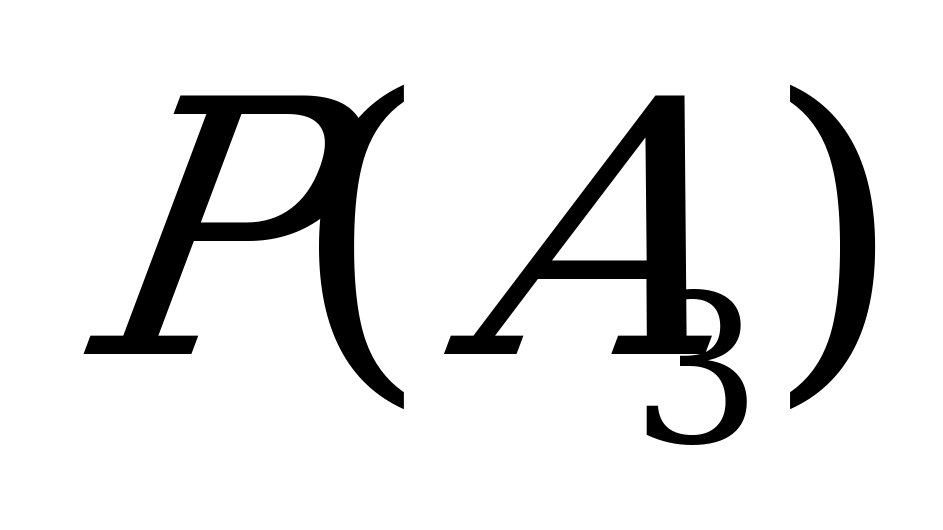 +
+ ·
·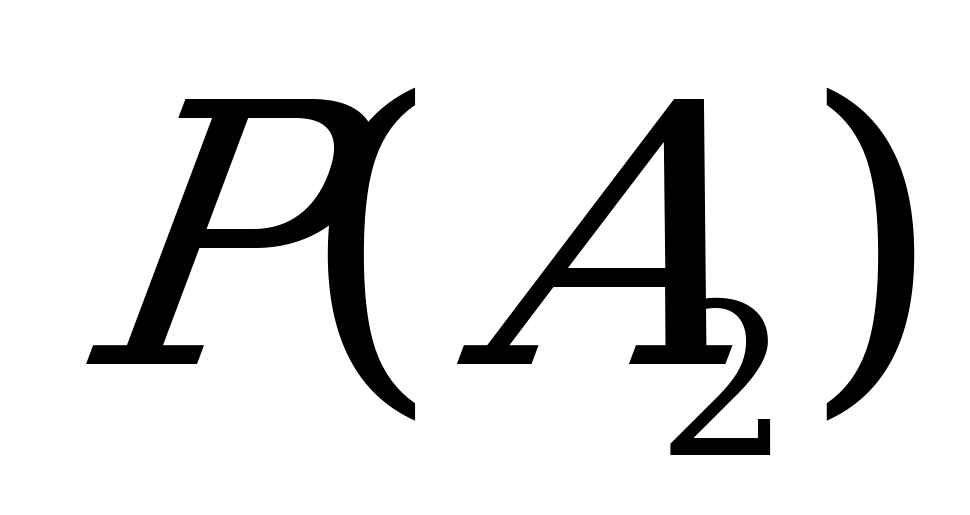 ·
·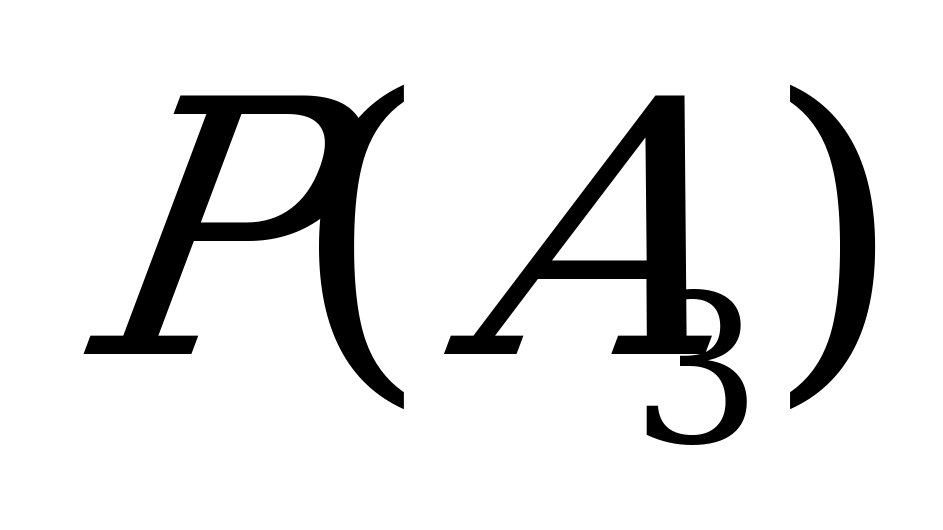 =
=
=0.7·0.8·0.1+0.7·0.2·0.9+0.3·0.8·0.9=0.056+0.126+0.216=0.398.
Вероятность поражения цели двумя пулями равна 0.398.
При вычислении вероятности события  можно рассуждать аналогично и получить ответ на вопрос последней задачи. Однако записи и вычисления при этом окажутся нерационально длинными. Поскольку в вопросе последней задачи имеются слова «…хотя бы одной…», рекомендуем воспользоваться следующим Правилом:
можно рассуждать аналогично и получить ответ на вопрос последней задачи. Однако записи и вычисления при этом окажутся нерационально длинными. Поскольку в вопросе последней задачи имеются слова «…хотя бы одной…», рекомендуем воспользоваться следующим Правилом:
Правило. При вычислении вероятности события  , в записи которого имеются слова «…хотя бы один…» или аналогичные им слова, рациональное решение требует перехода от этого события к противоположному событию
, в записи которого имеются слова «…хотя бы один…» или аналогичные им слова, рациональное решение требует перехода от этого события к противоположному событию  , содержащего слова «…ни одного…». После вычисления вероятности
, содержащего слова «…ни одного…». После вычисления вероятности  вероятность
вероятность  находится по формуле:
находится по формуле: 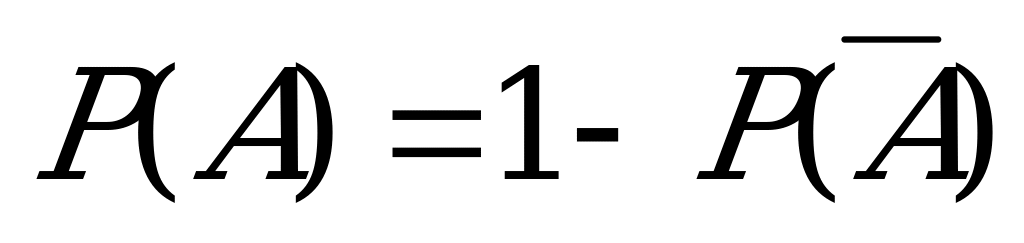 .
.
Перейдем к событию 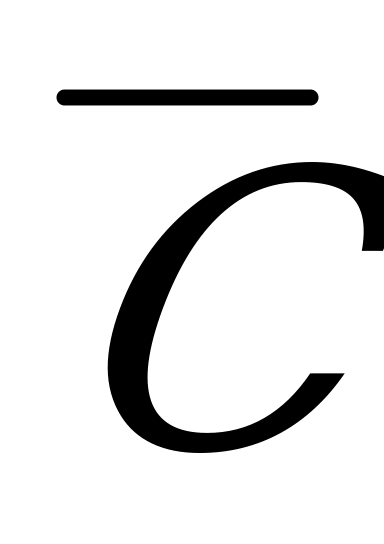 – (ни один из стрелков не попал)=(промахнулся первый стрелок) И (промахнулся второй стрелок) И (промахнулся третий стрелок):
– (ни один из стрелков не попал)=(промахнулся первый стрелок) И (промахнулся второй стрелок) И (промахнулся третий стрелок):
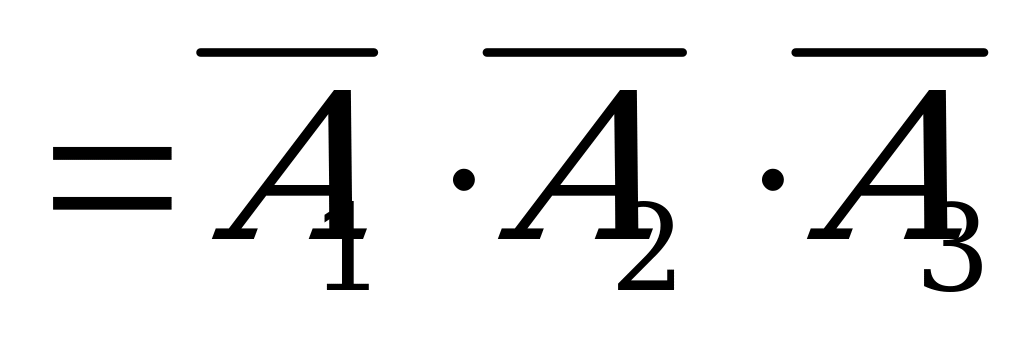 ,
,
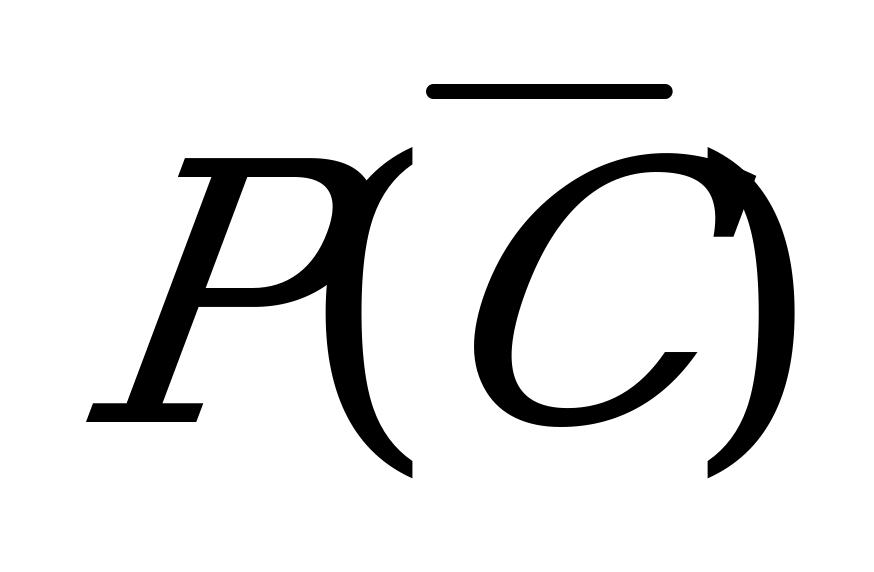
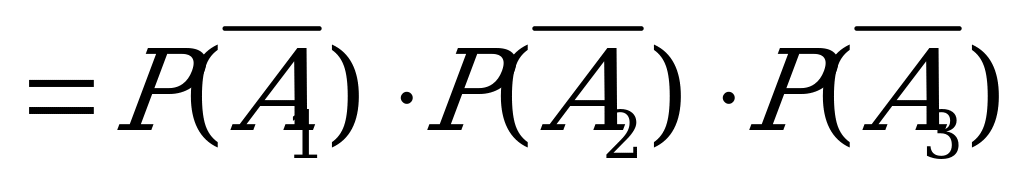 =0.3·0.2·0.1=0.006,
=0.3·0.2·0.1=0.006,
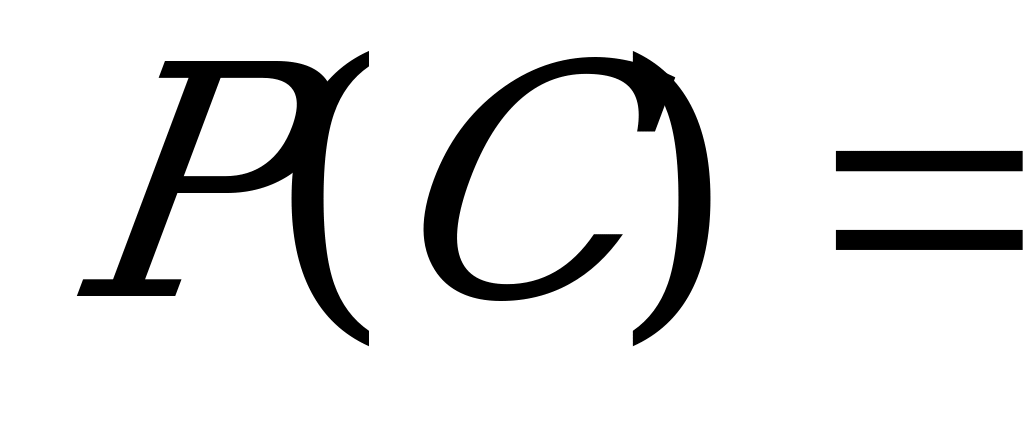 1-0.006=0.994.
1-0.006=0.994.
Вероятность поражения цели хотя бы одной пулей равна 0.994.
Задача 4. Футбольная команда играет 4 игры, причем вероятность выигрыша в каждой игре примерно одна и та же. Тренер рассчитывает, что вероятность победы хотя бы в одной игре равна 0.9744. Какова вероятность победы в одной игре?
Решение
Опыт: 4 раза проводится футбольный матч.
Событие  – выигрыш хотя бы в одной из 4 игр,
– выигрыш хотя бы в одной из 4 игр,  =0.9744.
=0.9744.
Событие  – проигрыш всех 4 игр=(проигрыш в первой игре) И (проигрыш во второй игре) И (проигрыш в третьей игре) И (проигрыш в четвертой игре).
– проигрыш всех 4 игр=(проигрыш в первой игре) И (проигрыш во второй игре) И (проигрыш в третьей игре) И (проигрыш в четвертой игре).
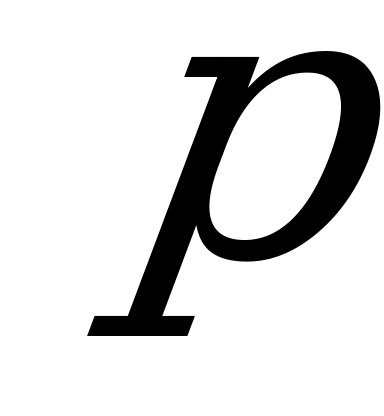 – вероятность победы в одной игре,
– вероятность победы в одной игре,
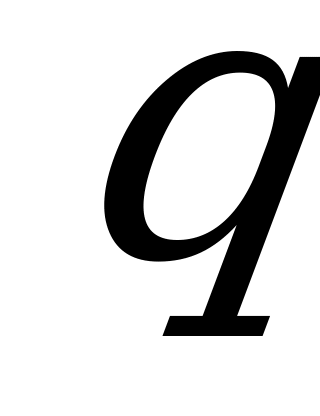 =1-
=1-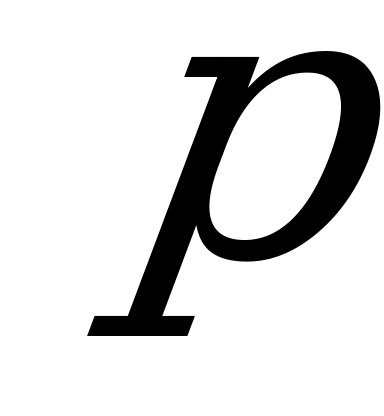 – вероятность проигрыша в одной игре.
– вероятность проигрыша в одной игре.
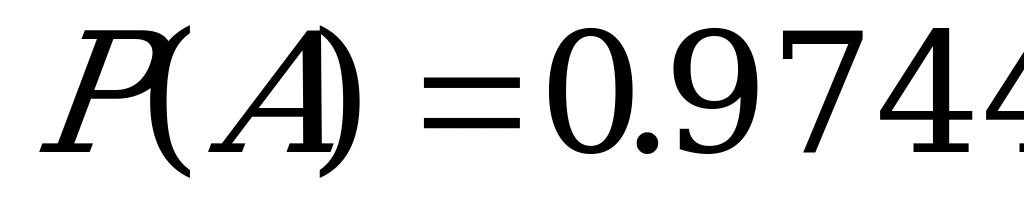 – вероятность выигрыша хотя бы в одной игре.
– вероятность выигрыша хотя бы в одной игре.
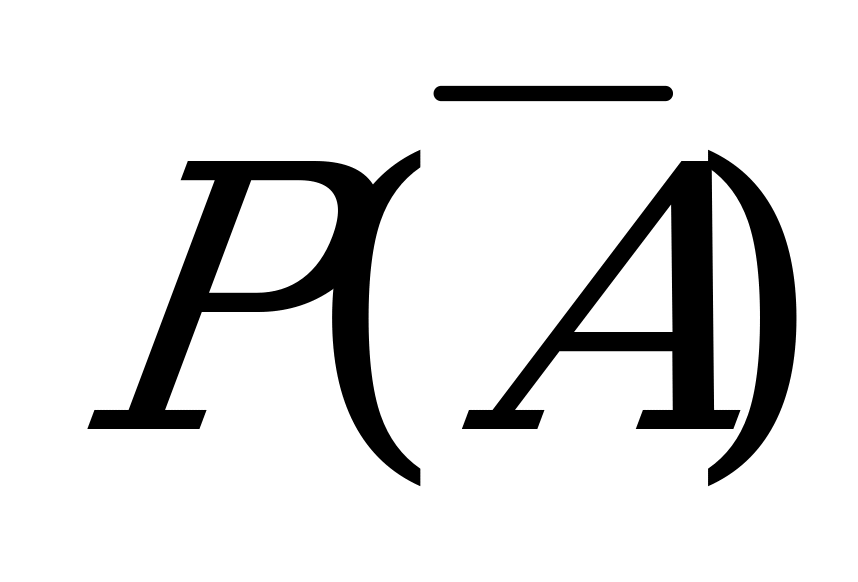 =1-0.9744=0.0256=
=1-0.9744=0.0256=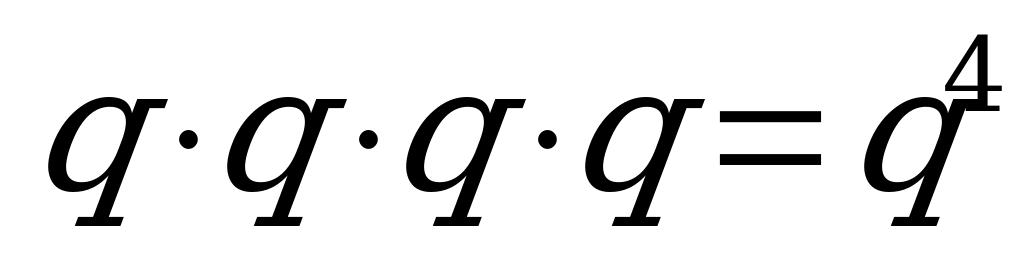 – вероятность проигрыша всех четырех игр.
– вероятность проигрыша всех четырех игр.
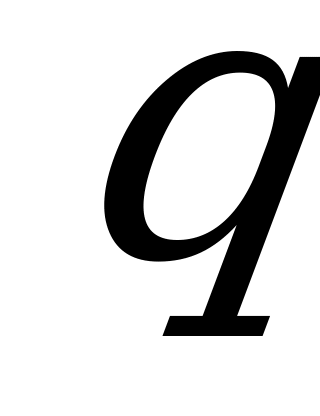
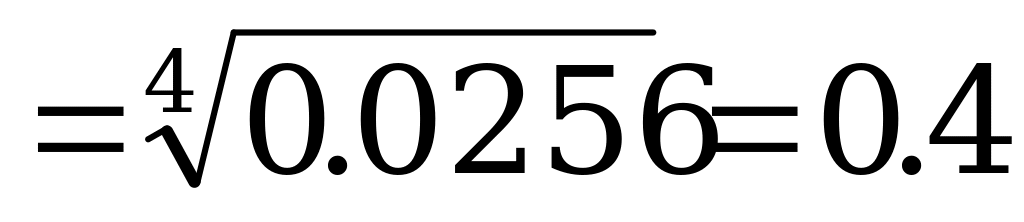 – вероятность проигрыша в одной игре.
– вероятность проигрыша в одной игре.
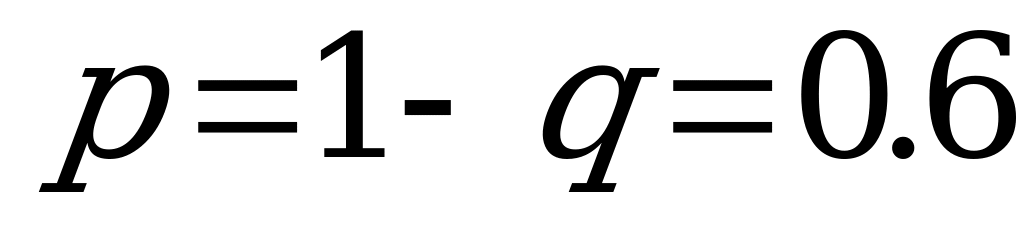 – вероятность выигрыша в одной игре.
– вероятность выигрыша в одной игре.
Задача 5.В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность поражения мишени при выстреле из винтовки с оптическим прицелом равна 0.95, без оптического прицела – 0.7. Найти вероятность поражения мишени, если стрелок произведет один выстрел из наудачу взятой винтовки.
Решение
Опыт: Взять наугад винтовку из пирамиды и произвести из нее выстрел.
 – поражение мишени из взятой винтовки.
– поражение мишени из взятой винтовки.
Событие  происходит совместно с одной из гипотез:
происходит совместно с одной из гипотез:
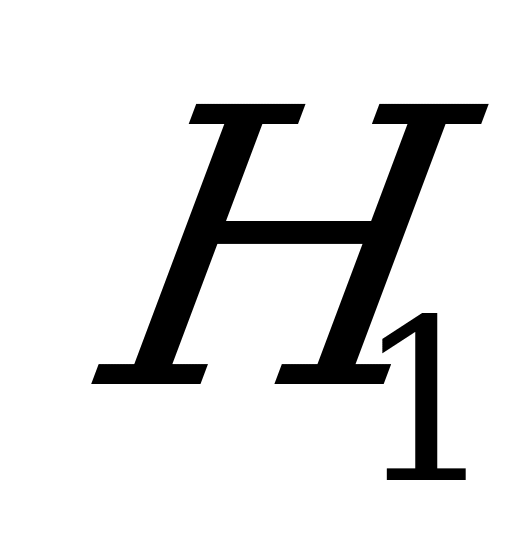 – взята винтовка с оптическим прицелом;
– взята винтовка с оптическим прицелом;
 – взята винтовка без оптического прицела.
– взята винтовка без оптического прицела.
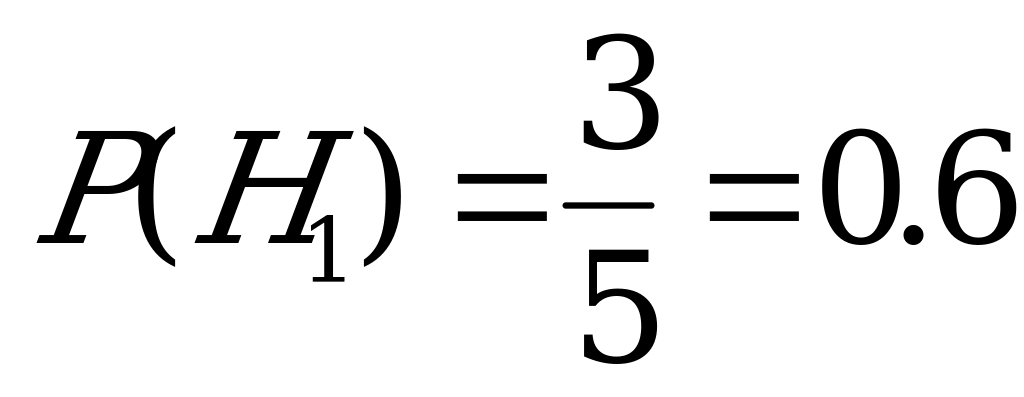 ,
, 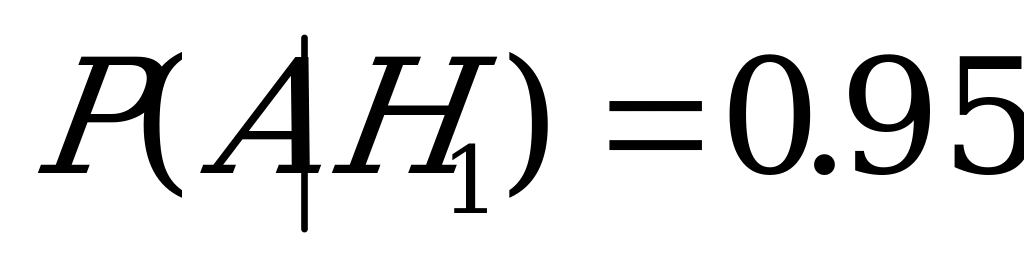 ;
;
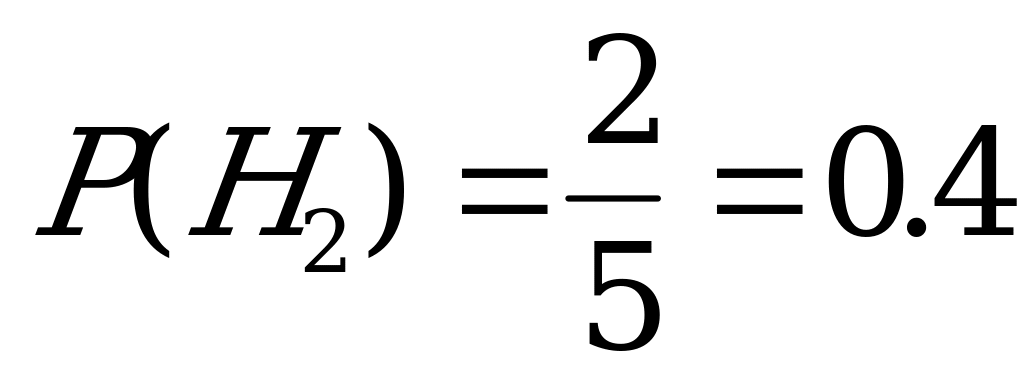 ,
, 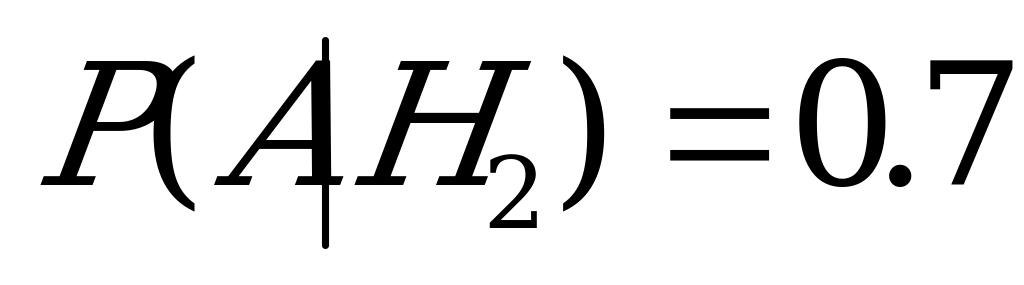 .
.
События 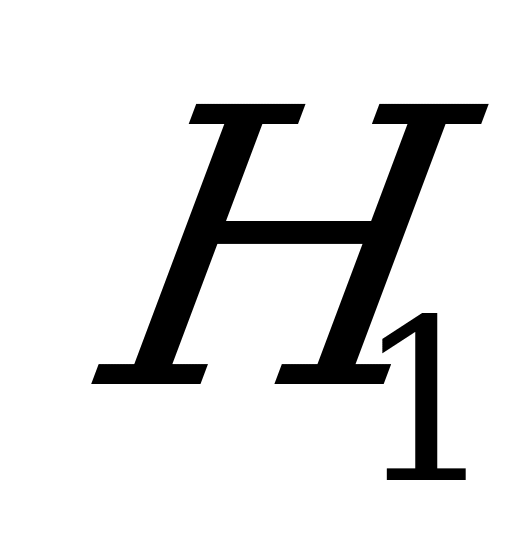 и
и  образуют полную группу событий, и задача решается по формуле полной вероятности:
образуют полную группу событий, и задача решается по формуле полной вероятности:
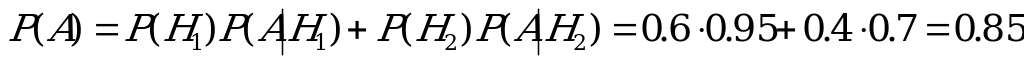 .
.
Задача 6.Детали изготавливаются на 3 станках, причем на первом станке изготавливается 50 % всех деталей, на втором 20%, остальные на третьем. Вероятность брака на первом станке – 0.03, на втором – 0.025, на третьем – 0.01. Взятая наугад деталь оказалась бракованой. Найти вероятность того, что она изготовлена на втором станке.
Решение
Опыт: Взять наугад деталь.
 – взята деталь с браком.
– взята деталь с браком.
Событие  происходит совместно с одной из гипотез:
происходит совместно с одной из гипотез:
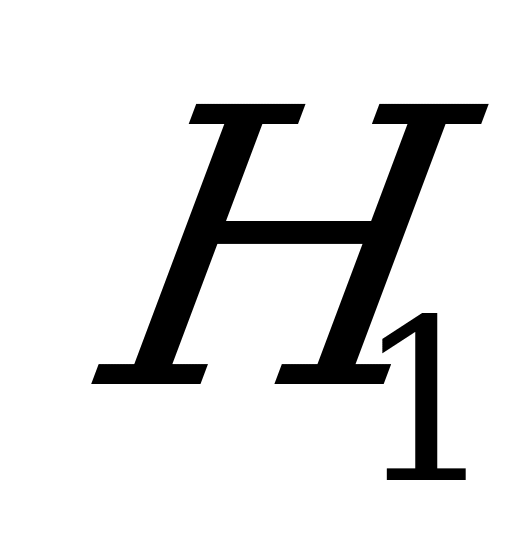 – взята деталь, изготовленная на первом станке;
– взята деталь, изготовленная на первом станке;
 – взята деталь, изготовленная на втором станке;
– взята деталь, изготовленная на втором станке;
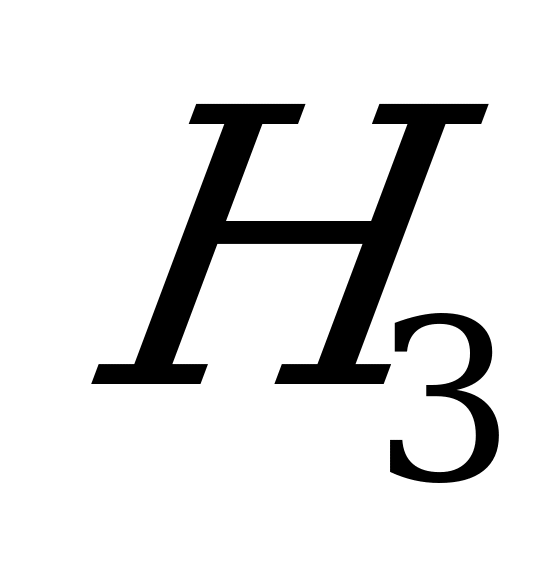 – взята деталь, изготовленная на третьем станке;
– взята деталь, изготовленная на третьем станке;
Требуется найти 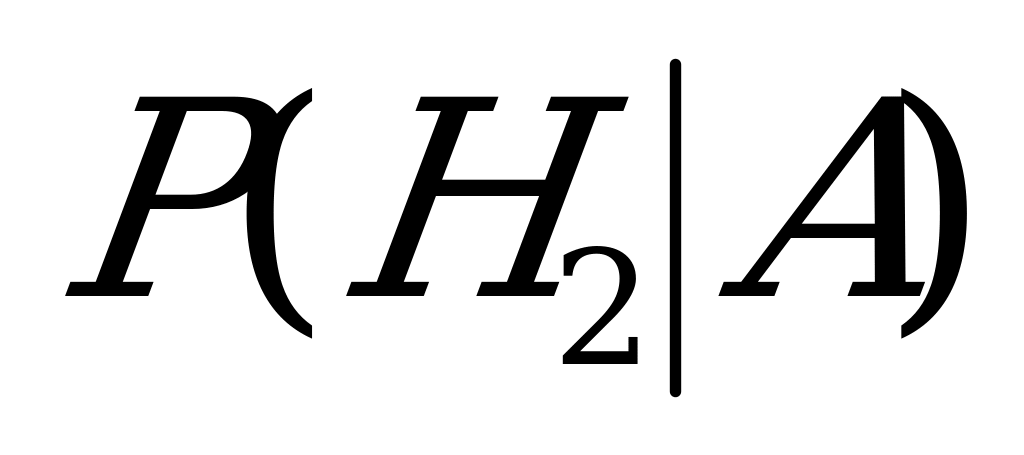 – вероятность того, что деталь, оказавшаяся бракованной, изготовлена на втором станке.
– вероятность того, что деталь, оказавшаяся бракованной, изготовлена на втором станке.
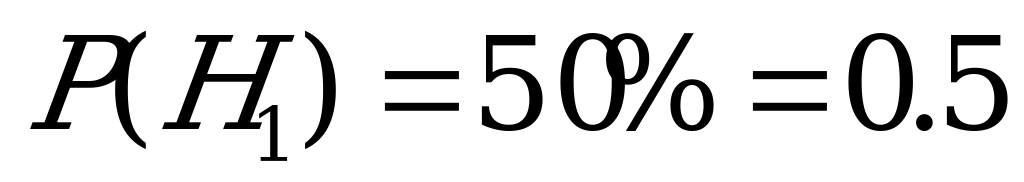 ,
, 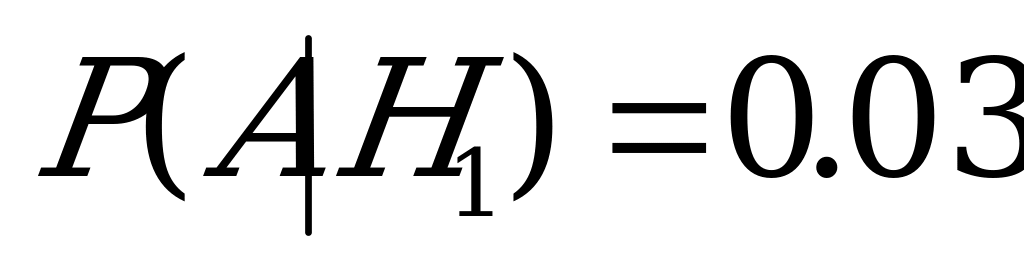 ;
;
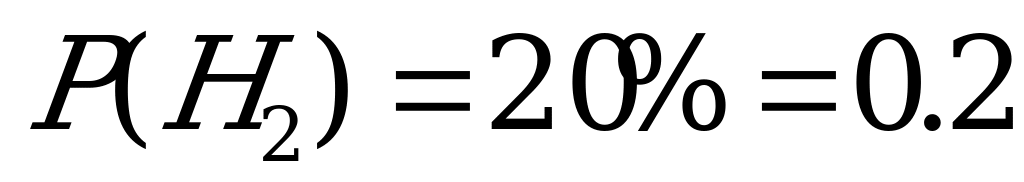 ,
, 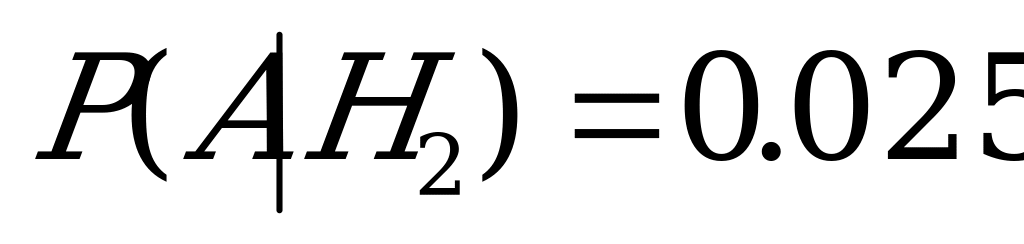 ;
;
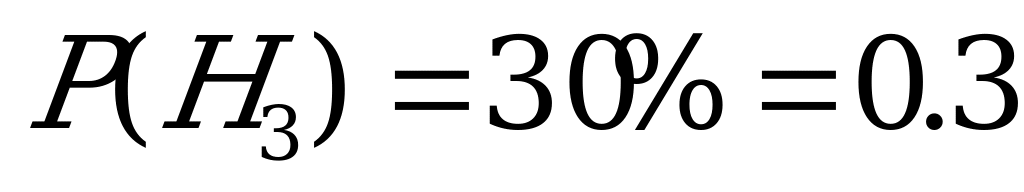 ,
, 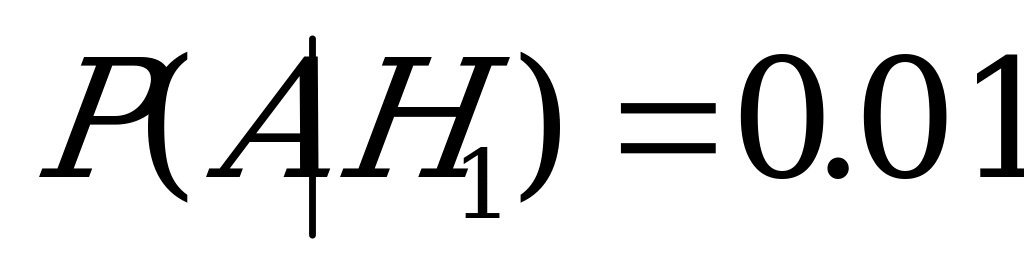 ;
;
События 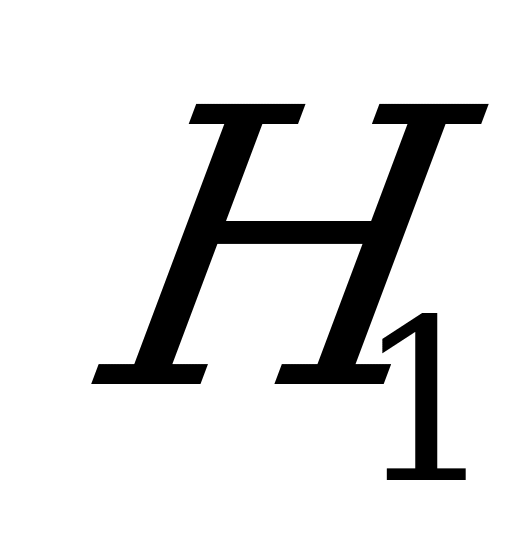 ,
,  и
и 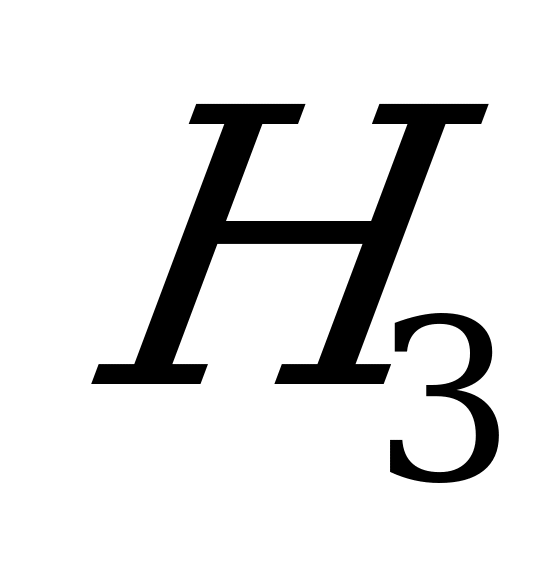 образуют полную группу событий. Задача решается по формуле Бейеса:
образуют полную группу событий. Задача решается по формуле Бейеса: 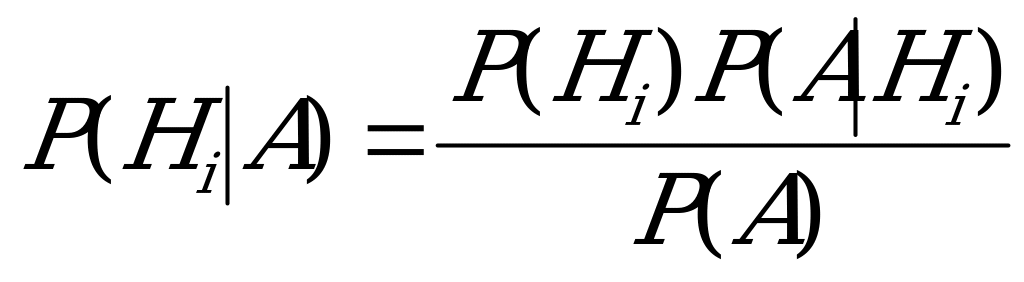 в два действия:
в два действия:
1. Найдем полную вероятность события  :
:
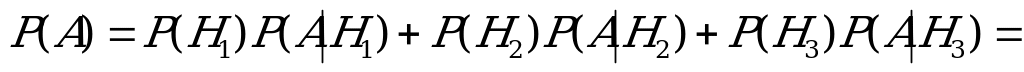
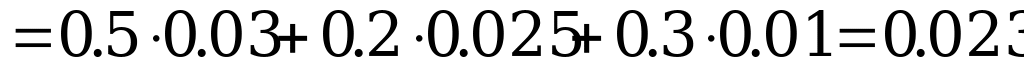 .
.
2. Найдем вероятность того, что вынутая бракованная деталь изготовлена на втором станке:
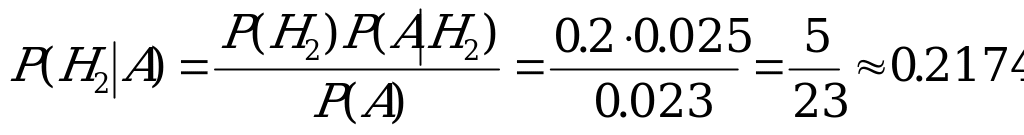 .
.
Задача 7.Монету бросают 6 раз. Найти вероятность того, что «герб» выпадет менее 2 раз. Составить ряд распределения случайной величины 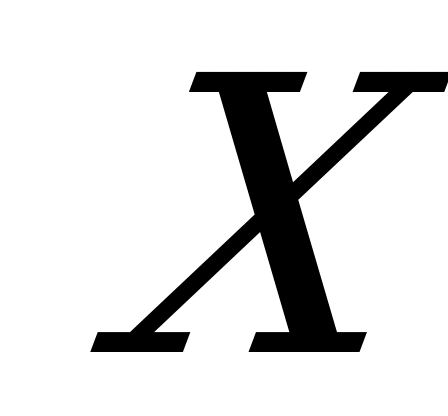 – число выпадений герба при шестикратном бросании монеты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. Построить гистограмму и многоугольник распределения.
– число выпадений герба при шестикратном бросании монеты. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. Построить гистограмму и многоугольник распределения.
Решение
Опыт: Монета брошена один раз.
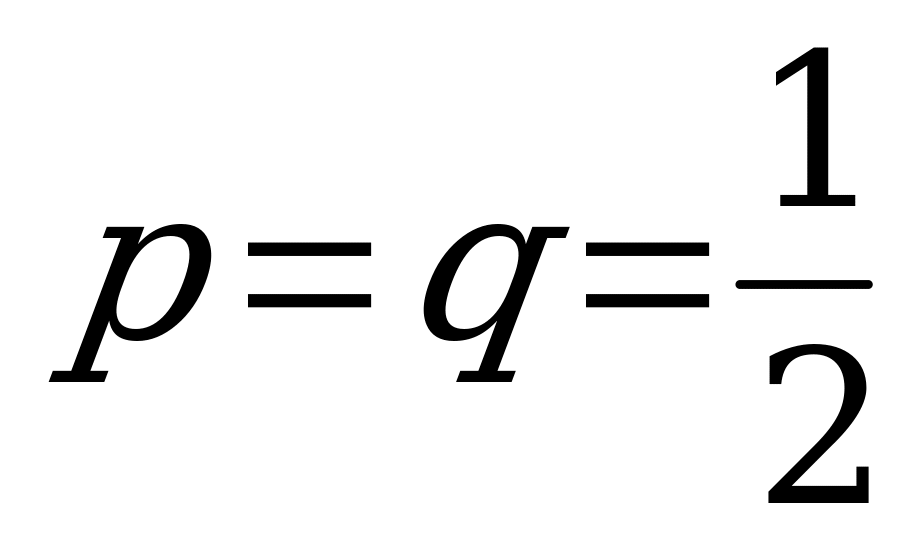 – вероятности выпадения герба и решетки при одном бросании.
– вероятности выпадения герба и решетки при одном бросании.
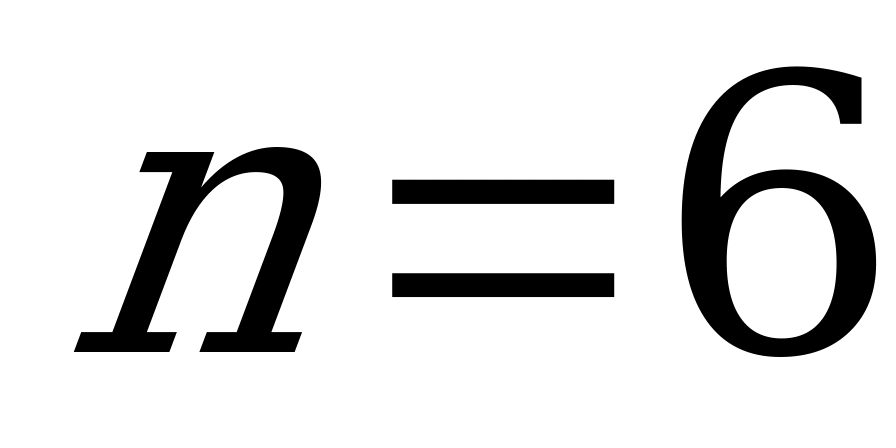 – столько раз повторен опыт.
– столько раз повторен опыт.
Воспользуемся формулой Бернулли:
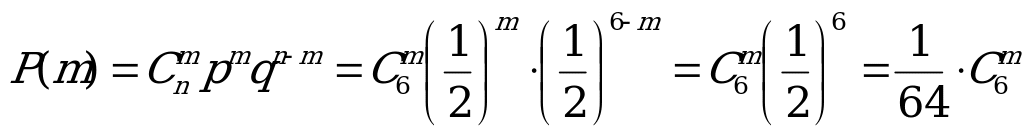 ,
,
и строкой треугольника Паскаля 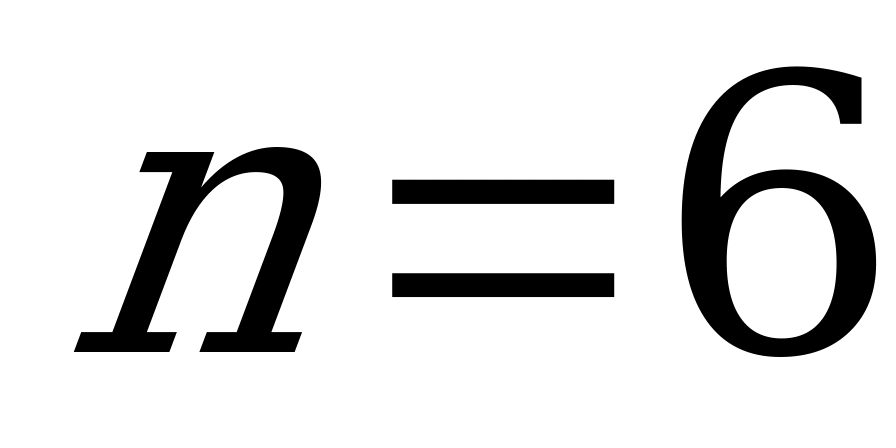 :
:
Получаем ряд распределения случайной величины 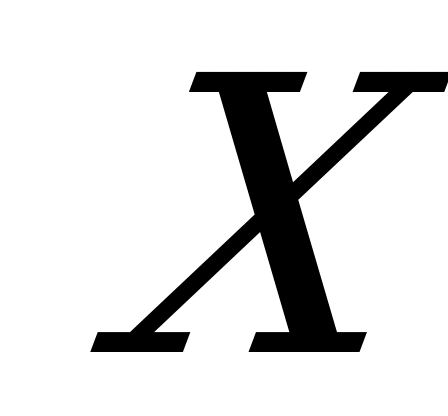 – число выпадений герба при шестикратном бросании монеты (первая и вторая строки) и функцию распределения (первая и третья строки):
– число выпадений герба при шестикратном бросании монеты (первая и вторая строки) и функцию распределения (первая и третья строки):
| 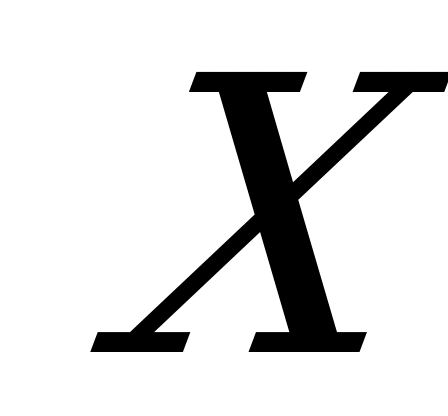 – число выпадений герба при шестикратном бросании монеты, – число выпадений герба при шестикратном бросании монеты, 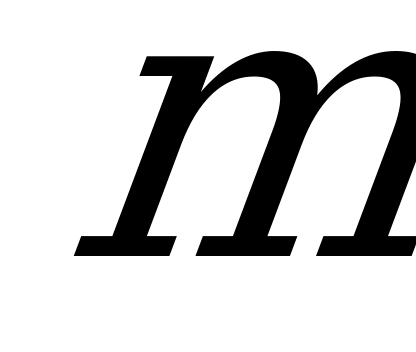
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 6 |
| Вероятность 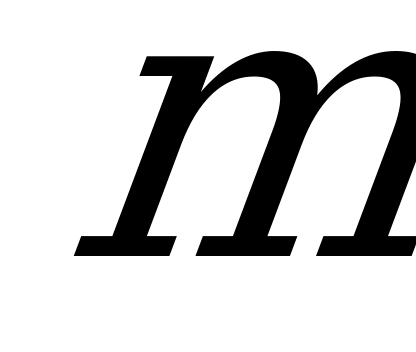 -кратного выпадения монеты, -кратного выпадения монеты,  | 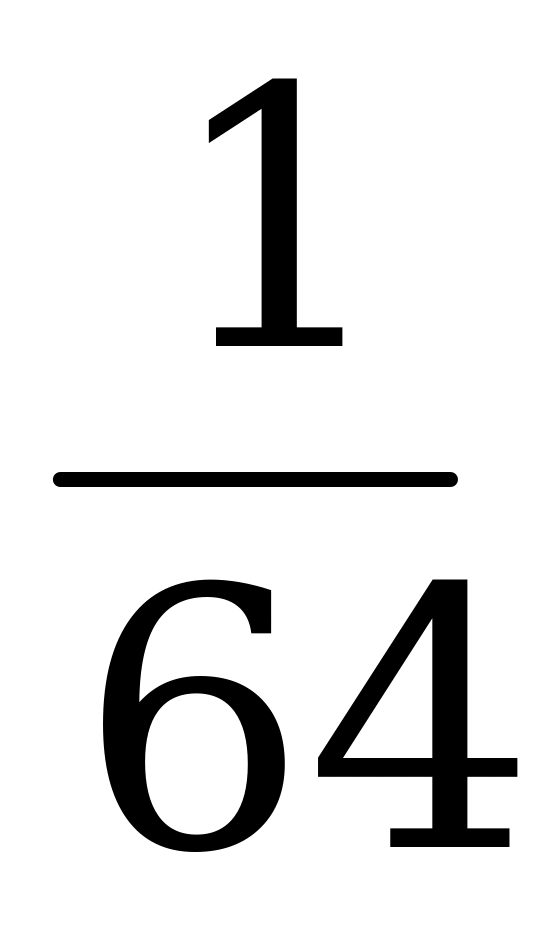
| 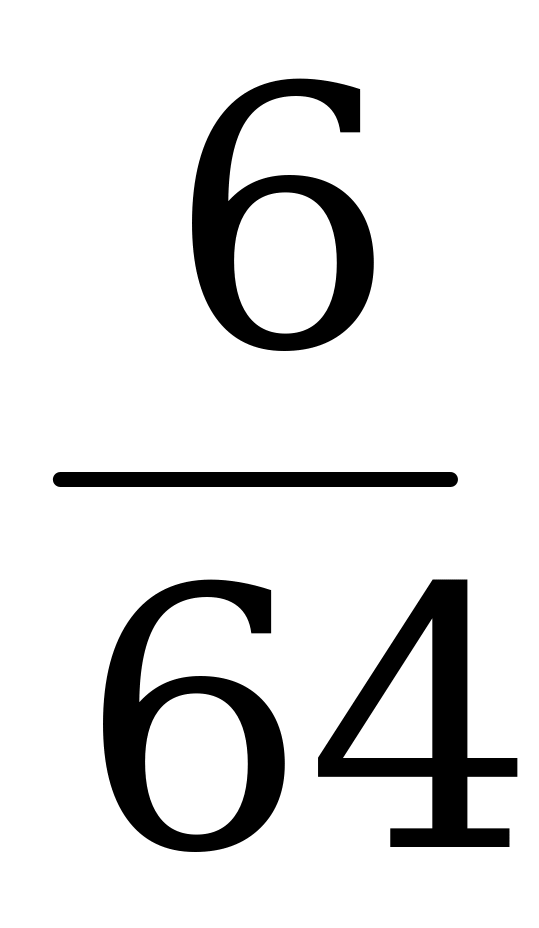
| 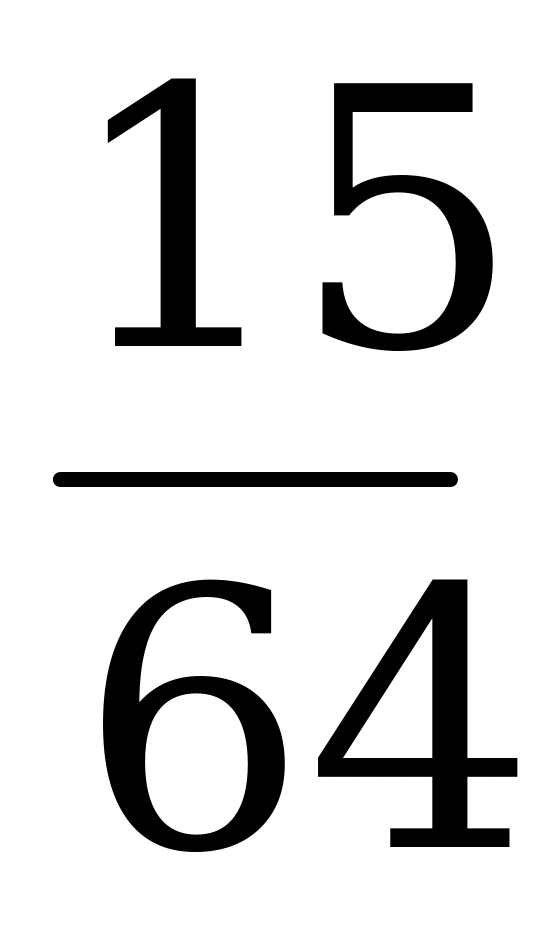
| 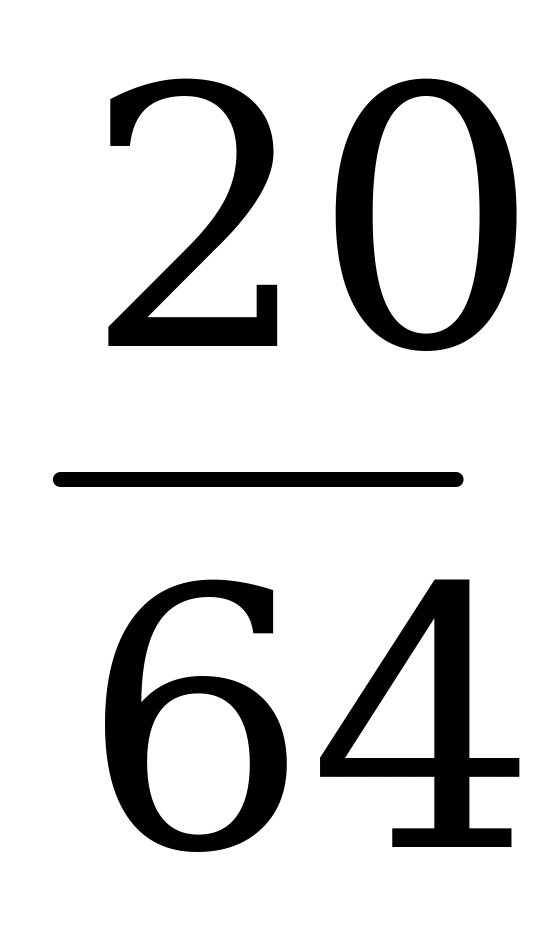
| 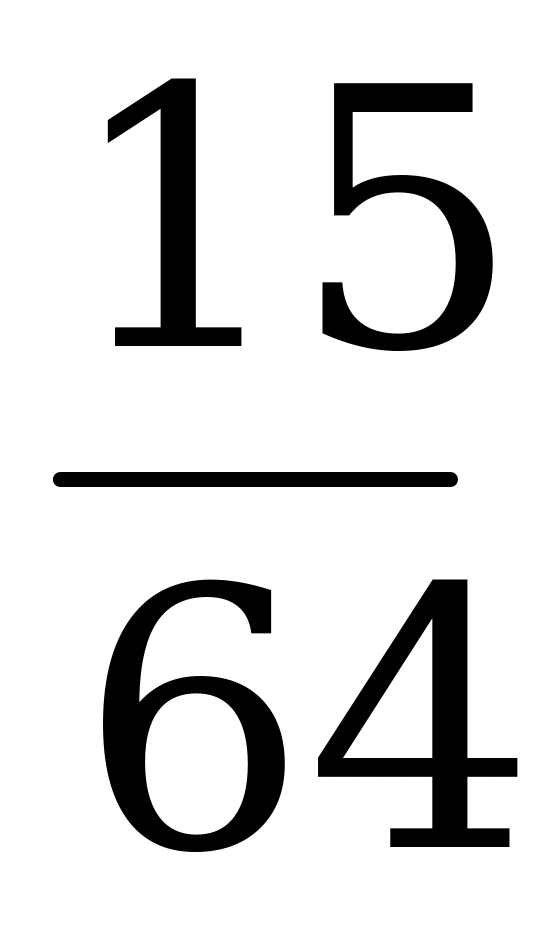
| 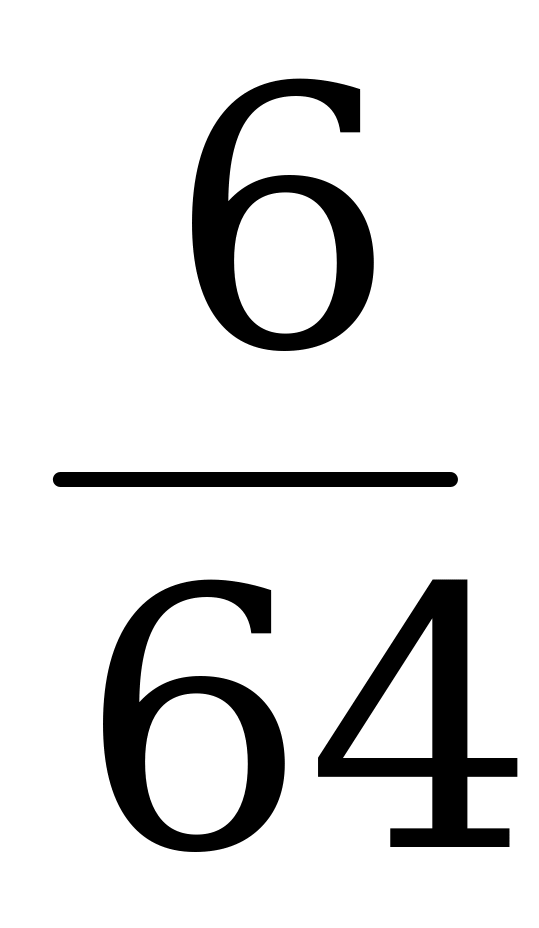
| 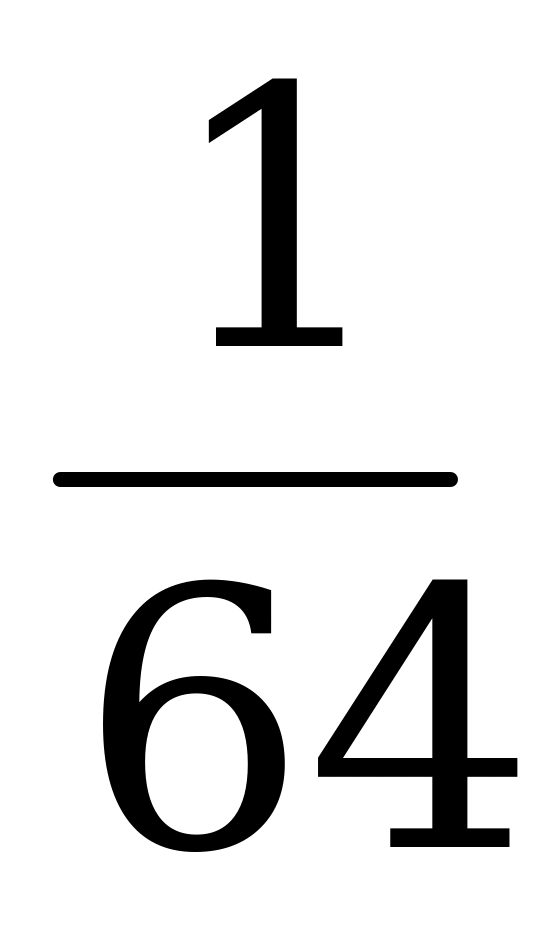
| 0 |
| Значения функции распределения, 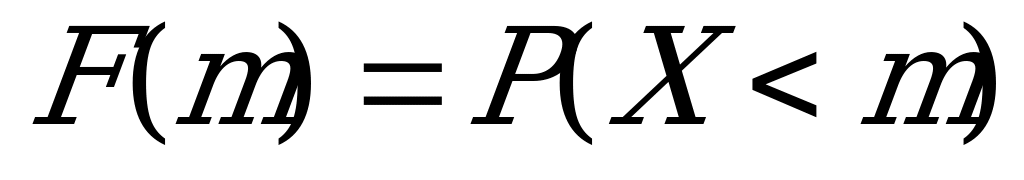 | 0 | 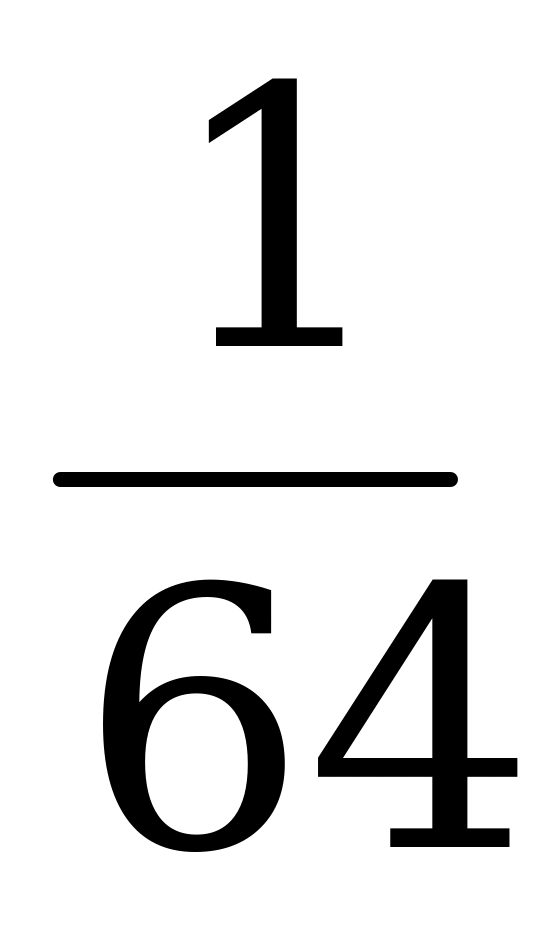
| 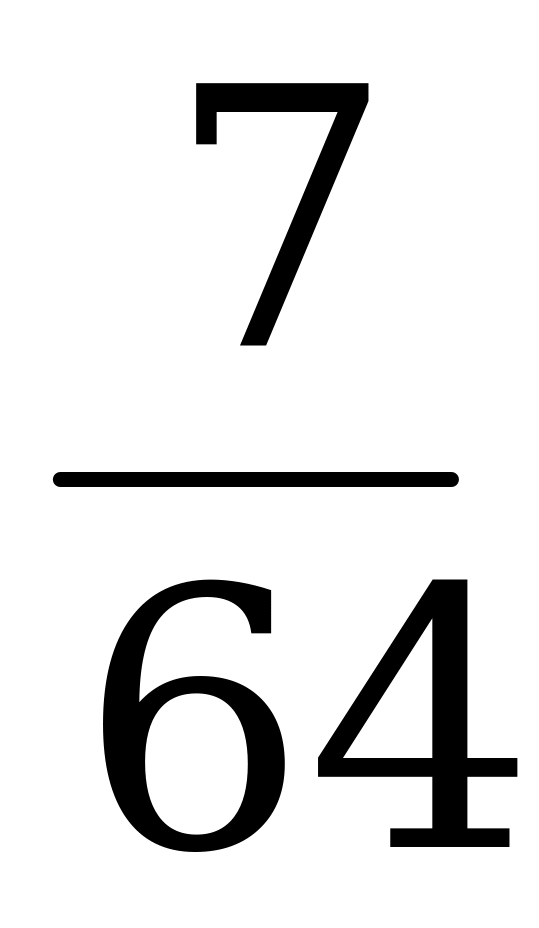
| 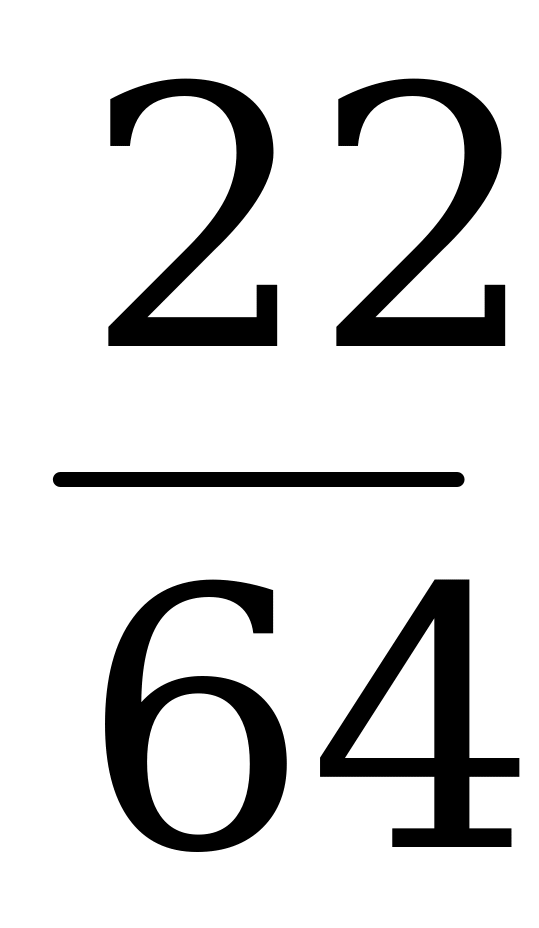
| 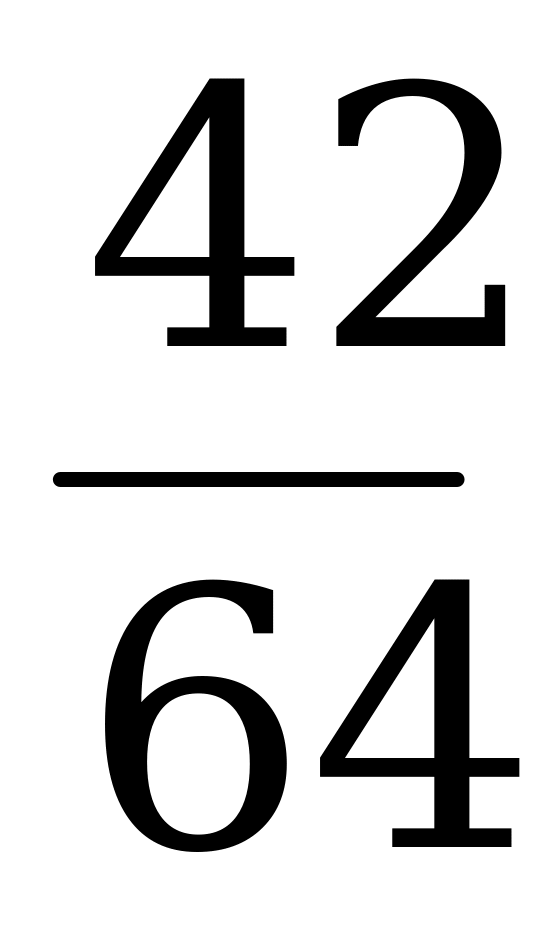
| 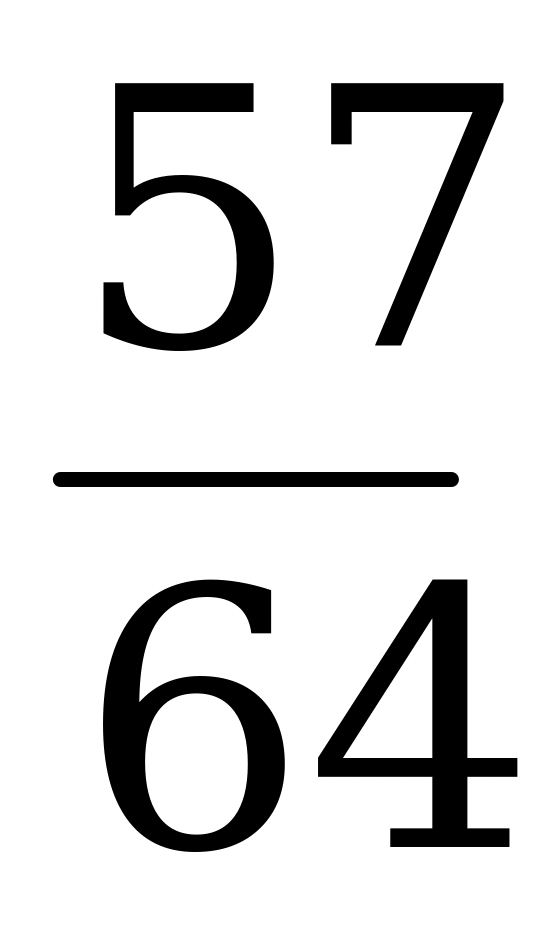
| 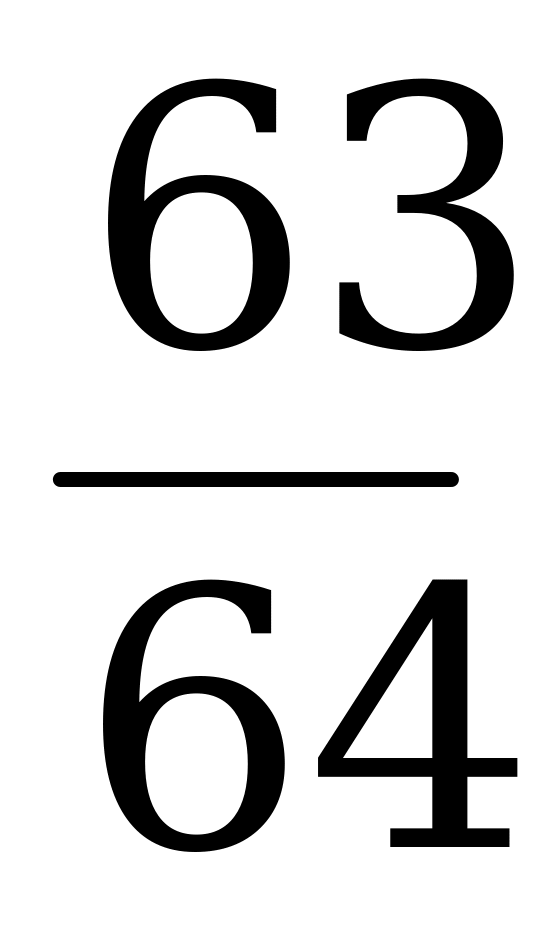
| 1 |
Найдем 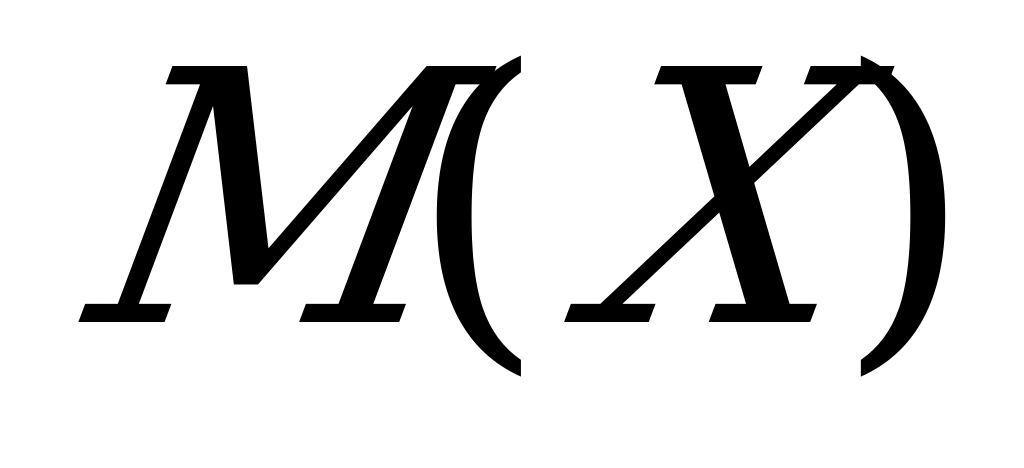 ,
, 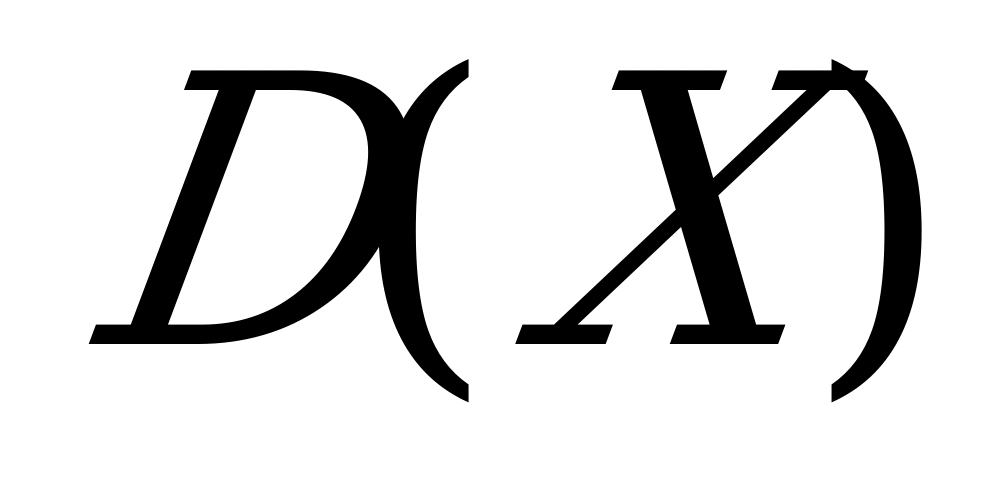 ,
, 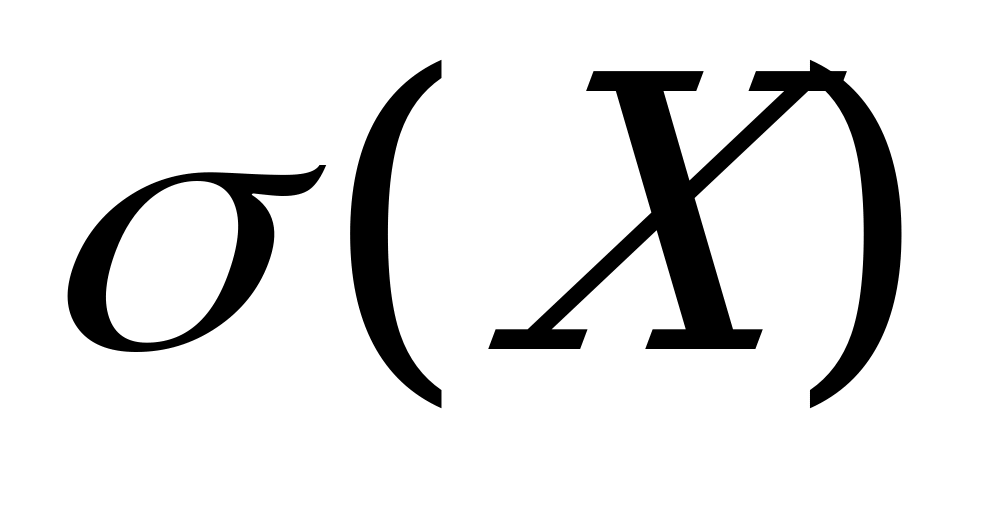 .
.
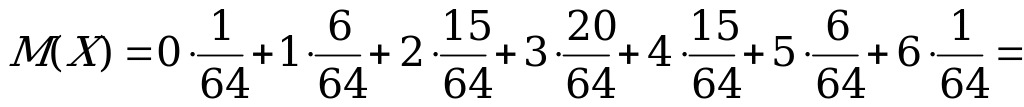
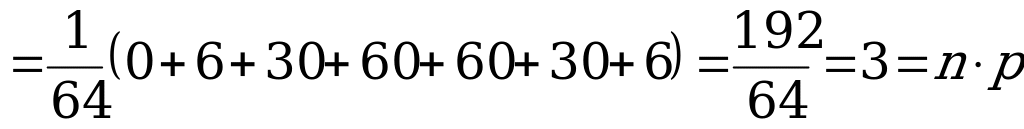 .
.
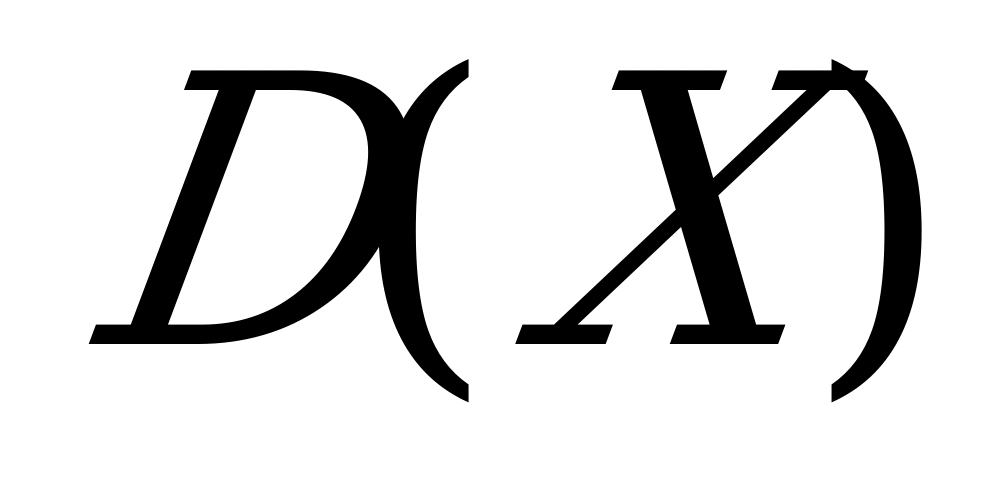
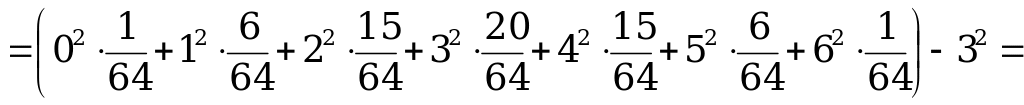
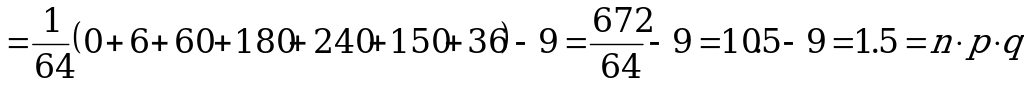 .
.
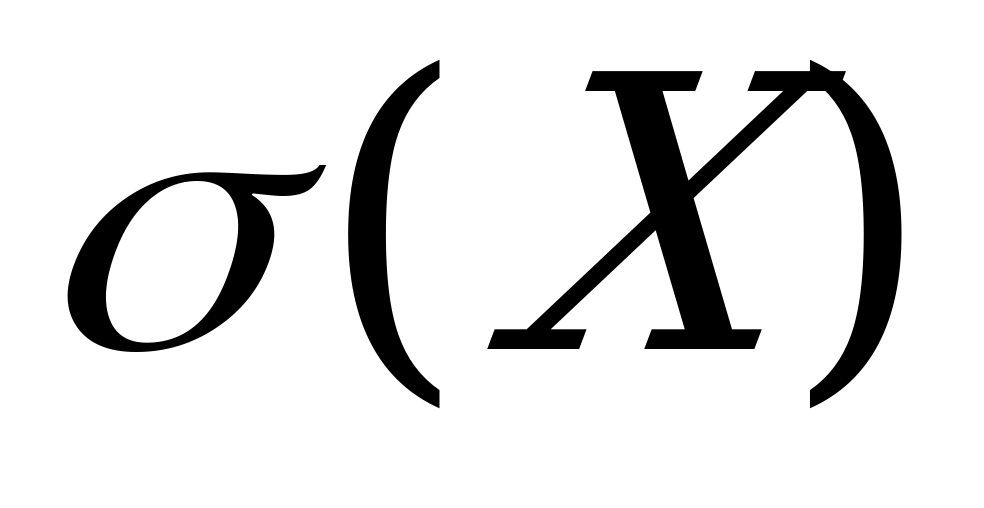
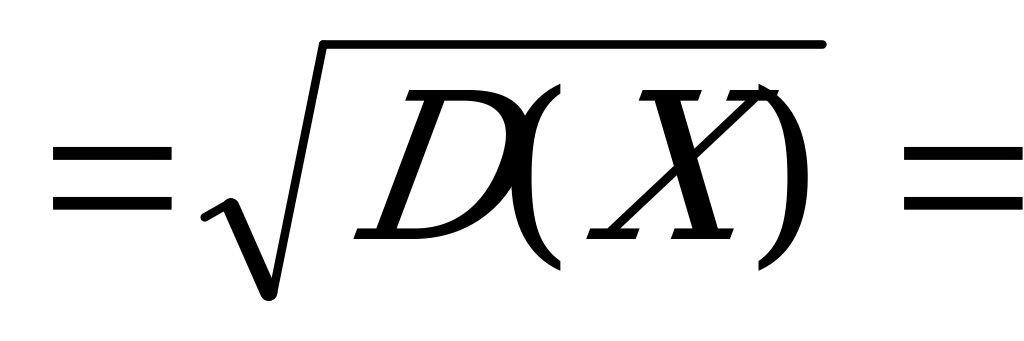
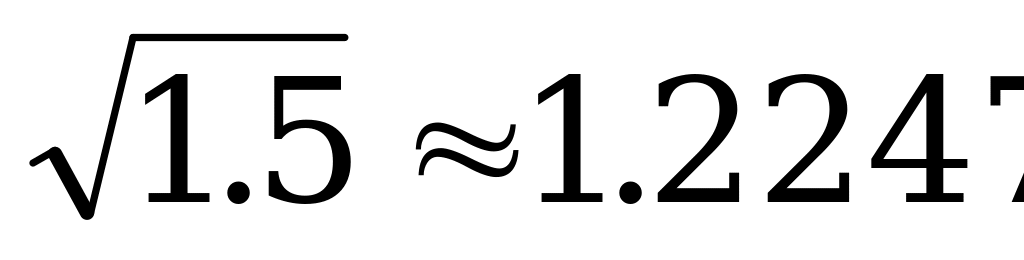 .
.
31







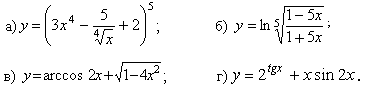
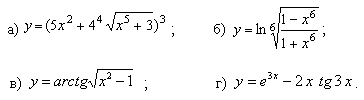
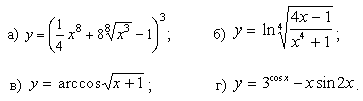
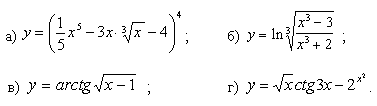
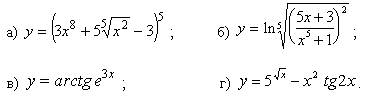
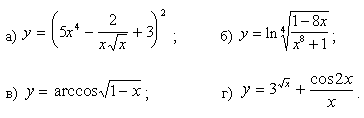
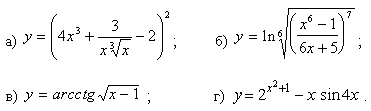
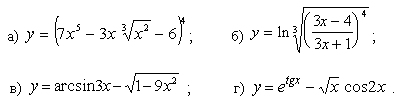
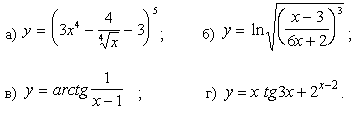
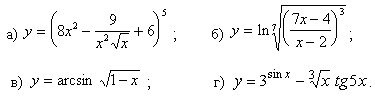
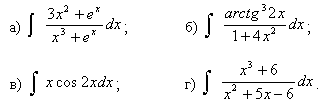
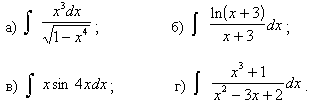
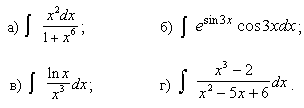
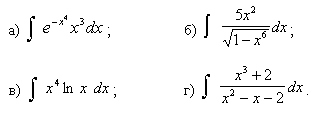
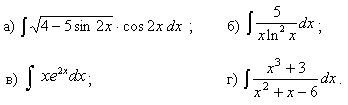
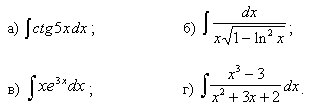
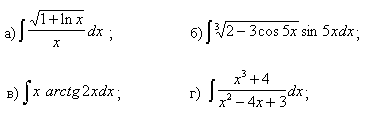
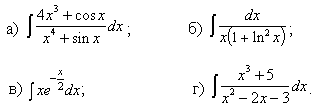
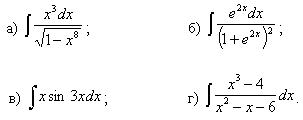
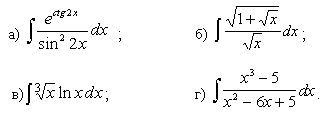
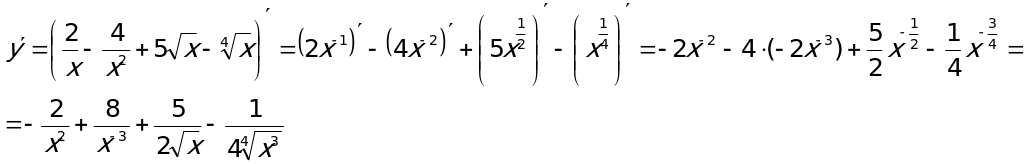 Пример 2. Вычислить производную функции.
Пример 2. Вычислить производную функции. 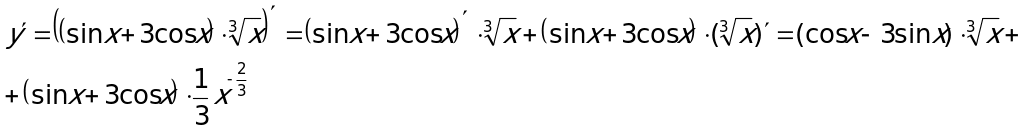 (дальнейшие преобразования в этих примерах можно не проводить).
(дальнейшие преобразования в этих примерах можно не проводить).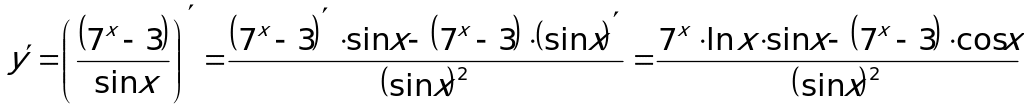 .
.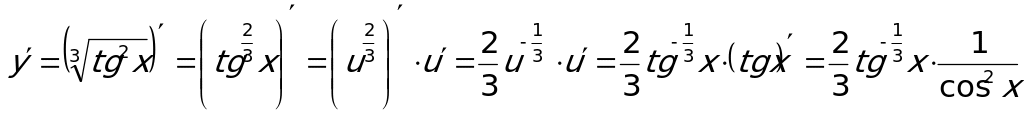 .
.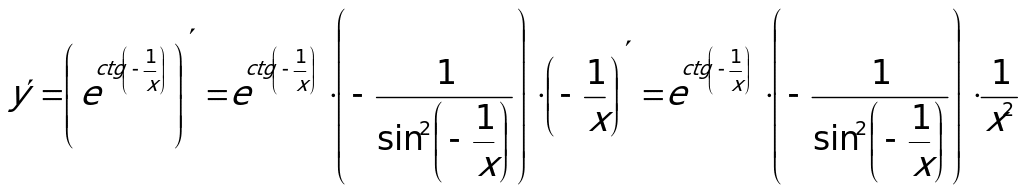
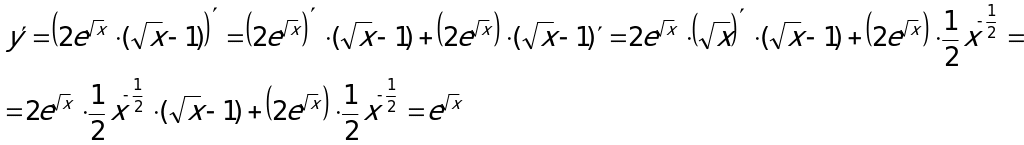 Пример 7. Вычислить производную функции
Пример 7. Вычислить производную функции