Контрольная работа по теме «Параллельные прямые»
Вариант 1
-
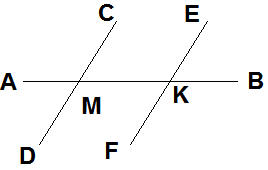
Запишите два накрест лежащих угла, два соответственных угла и два внутренних односторонних угла.
Решение.
-
DMK и  EKM – накрест лежащие углы,
EKM – накрест лежащие углы,
-
СМК и  МКЕ – внутренние односторонние углы,
МКЕ – внутренние односторонние углы,
-
СМК и  ЕКВ – соответственные углы.
ЕКВ – соответственные углы.
-
а‖b,  1 = 130°. с – секущая. Найдите
1 = 130°. с – секущая. Найдите  2.
2.
| 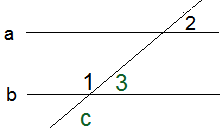
| Дано: а‖b, с – секущая,  1 = 130°. 1 = 130°.
Найдите:  2. 2. |
Решение.
-
а‖b, с – секущая  2 =
2 =  3 (как соответственные углы).
3 (как соответственные углы).
-
 1 = 130°,
1 = 130°,  1 и
1 и  3 – смежные. Сумма смежных углов рана 180°.
3 – смежные. Сумма смежных углов рана 180°.
 1 +
1 +  3 = 180°,
3 = 180°,  3 = 180° -
3 = 180° -  1,
1,  3 = 180° - 130°,
3 = 180° - 130°,  3 = 50°.
3 = 50°.
Ответ: 50°.
-
Прямые AB и CD параллельны, MN – секущая. Два внутренних односторонних угла относятся как 2 : 3. Найдите все углы, образованные параллельными прямыми и секущей.
| 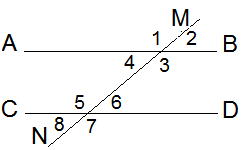
| Дано: AB‖CD, MN – секущая,  6 : 6 :  3 = 2 : 3. 3 = 2 : 3.
Найдите:  1, 1,  2, …, 2, …, 8 8 |
Решение.
-
AB‖CD, MN – секущая,  6 и
6 и  3 – внутренние односторонние.
3 – внутренние односторонние.
 6 +
6 +  3 = 180°,
3 = 180°,  6 +
6 +  3 – составляют 5 частей
3 – составляют 5 частей
(по условию  6 :
6 :  3 = 2 : 3).
3 = 2 : 3).
1 часть = 180° : 5 =36°,  6 = 36°∙2 = 72°,
6 = 36°∙2 = 72°,  3 = 36°∙ 3 = 108°,
3 = 36°∙ 3 = 108°,
 3 =
3 =  5 = 108°,
5 = 108°,  6 =
6 =  4= 72° - внутренние накрест лежащие,
4= 72° - внутренние накрест лежащие,
 3=
3=  7 = 108°,
7 = 108°,  5 =
5 =  1 = 108° - соответственные,
1 = 108° - соответственные,
 6 =
6 =  2= 72°,
2= 72°,  8 =
8 =  4= 72°- соответственные.
4= 72°- соответственные.
Ответ:  1=
1=  3=
3= 5=
5= 7= 108°,
7= 108°,  2 =
2 =  4=
4= 6 =
6 = 8 = 72°.
8 = 72°.
-
В треугольнике ABC равны стороны АС и ВС. На сторне АС взята точка М и проведена прямая, параллельная ВС, которая пересекает сторону АВ в точке К. Докажите, что ∆АМК – равнобедренный.
| 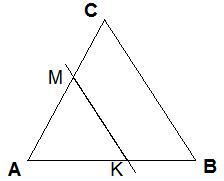
| Дано: ∆ABC, AС = CB, М € AC, К € AB, МК‖CB Доказать: ∆АМК – равнобедренный |
Доказательство:
-
МК‖CB, АВ – секущая,  МКА =
МКА =  СВA (как соответственные).
СВA (как соответственные).
-
В ∆ABC, AС = CB (по условию), отсюда следует, что ∆ABC – равнобедренный.
 САВ =
САВ =  СВА (как углы при основании равнобедренного треуголника).
СВА (как углы при основании равнобедренного треуголника).
-
Так как  МКА =
МКА =  СВA, то
СВA, то  МКА =
МКА =  САВ, значит
САВ, значит
∆АМК – равнобедренный
-
Дан четырехугольник АВСD. Известно, что АВ‖CD, BC‖AD. Докажите, что биссектрисы углов А и С параллельны.
| 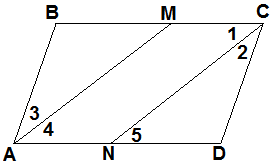
| Дано: ABCD – четырехугольник, АВ‖CD, BC‖AD, АМ – биссектриса  А, СN – биссектриса А, СN – биссектриса  C, C,
Доказать: АМ‖СN |
Доказательство:
-
BC‖AD (по условию), СD - секущая,  BCD +
BCD +  ADC = 180° (1) (как внутренние односторонние),
ADC = 180° (1) (как внутренние односторонние),
-
АВ‖CD (по условию), АD – секущая,  ВAD +
ВAD +  ADC = 180° (как внутренние односторонние),
ADC = 180° (как внутренние односторонние),
тогда  BАD =
BАD =  BCD (
BCD ( ADC – общий угол).
ADC – общий угол).
-
 4 = �
4 = � �
�  ВAD
ВAD
-
 5 =
5 =  1 (накрест лежащие при ВС‖AD и CN – cекущей),
1 (накрест лежащие при ВС‖AD и CN – cекущей),
-
 4 =
4 =  5 (как соответственные при АМ, СN и АN – cекущей).
5 (как соответственные при АМ, СN и АN – cекущей).
Если при пересечении двух прямых (АМ и СN) секущей (АN) соответственные углы равны, то прямые АМ‖СN.
Что и требовалось доказать.
Контрольная работа по теме «Параллельные прямые»
Вариант 2
-
Запишите два накрест лежащих угла, два соответственных угла и два внутренних односторонних угла.
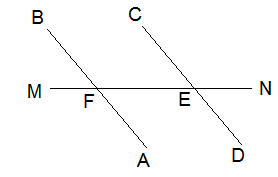
Решение.
-
BFE и  FED – накрест лежащие углы,
FED – накрест лежащие углы,
-
AFE и  DEF – внутренние односторонние углы,
DEF – внутренние односторонние углы,
-
MFB и  FEC – соответственные углы.
FEC – соответственные углы.
-
с‖d,  1 = 45°. Найдите
1 = 45°. Найдите  2.
2.
| 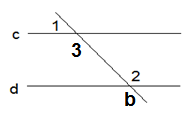
| Дано: с‖d, b – секущая,  1 = 45°. 1 = 45°.
Найдите:  2. 2. |
Решение.
-
с‖d, с – секущая,  2,
2,  3 – внутренние накрест лежащие углы. Если две параллельные прямые прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
3 – внутренние накрест лежащие углы. Если две параллельные прямые прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.  2 =
2 =  3.
3.
2)  1 = 45°,
1 = 45°,  1 и
1 и  3 - смежные,
3 - смежные,  1 +
1 +  3 = 180°,
3 = 180°,  3 = 180° -
3 = 180° -  1,
1,
 3 = 180° - 45° = 135°,
3 = 180° - 45° = 135°,  2 =
2 =  3 = 135°.
3 = 135°.
Ответ: 135°.
-
Прямые AB и CD параллельны, NP – секущая. Разность двух внутренних односторонних углов равна 40°. Найдите все углы, образованные параллельными прямым и секущей.
| 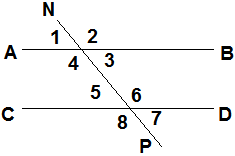
| Дано: AB‖CD, NP – секущая,  4 - 4 -  5 = 40°. 5 = 40°.
Найдите:  1, 1,  2, …, 2, …, 8 8 |
Решение.
-
AB‖CD, NP – секущая,  4 +
4 +  5 = 180° (как внутренние односторонние).
5 = 180° (как внутренние односторонние).
Если две параллельные прямые прямые пересечены третьей прямой, то сумма градусных мер внутренних односторонних углов равна 180°.
 4 -
4 -  5 = 40° (по условию),
5 = 40° (по условию),
2  4 = 220°,
4 = 220°,  4 = 220° : 2= 110°,
4 = 220° : 2= 110°,
 5 = 110° - 40° = 70°
5 = 110° - 40° = 70°
 5 =
5 = 3 = 70°,
3 = 70°,  6 =
6 =  4= 110° - внутренние накрест лежащие,
4= 110° - внутренние накрест лежащие,
 3 =
3 =  7 = 70°,
7 = 70°,  5 =
5 =  1 = 70° - соответственные,
1 = 70° - соответственные,
 6 =
6 =  2 = 110°,
2 = 110°,  8 =
8 =  4= 110°- соответственные.
4= 110°- соответственные.
Ответ:  1 =
1 = 3 =
3 = 5 =
5 = 7 = 70°,
7 = 70°,  2 =
2 = 4 =
4 = 6 =
6 = 8 = 110°.
8 = 110°.
-
В треугольнике MNK равны стороны MN и NK. На сторне MN взята точка A. Через точку А проведена прямая, параллельная NK, которая пересекает сторону MK в точке B. Докажите, что ∆МAB – равнобедренный.
| 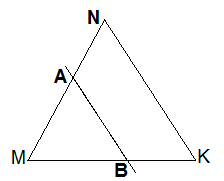
| Дано: ∆MNK, MN = NK, A € MN, B € MK, NК‖AB Доказать: ∆МАB – равнобедренный |
Доказательство:
-
∆MNK, MN = MK, то ∆MNK – равнобедренный.  NМК =
NМК =  NКМ (как углы при основании равнобедренного треуголника),
NКМ (как углы при основании равнобедренного треуголника),
-
AB‖NK, MK – секущая,  NКМ и
NКМ и  ABM – соответственные.
ABM – соответственные.
Если две параллельные прямые прямые пересечены третьей прямой, то соответственные углы равны, поэтому  NКМ =
NКМ =  ABM.
ABM.
-
Так как  NМК =
NМК =  NКМ, то
NКМ, то  ABM =
ABM =  NМК, значит
NМК, значит
∆МАB – равнобедренный
-
Дан четырехугольник MNPK. Известно, что MN‖PK, NP‖MK. Докажите, что биссектрисы углов N и K параллельны.
| 
| Дано: MNPK – четырехугольник, MN‖PK, MP‖MK, NC - биссектриса  N, N, KB – биссектриса  К, К, Доказать:NC‖KB |
Доказательство:
-
NP‖MK (по условию), PK - секущая, то  NPK +
NPK +  PKM = 180° (как внутренние односторонние),
PKM = 180° (как внутренние односторонние),
-
MN‖PK (по условию), MK - секущая, то  NMK +
NMK +  PKM = 180° (как внутренние односторонние), тогда
PKM = 180° (как внутренние односторонние), тогда  NPK =
NPK =  NMK (
NMK ( TPR – общий угол).
TPR – общий угол).
-
 3 = �
3 = � �
�  PKM ,
PKM ,
 2 = �
2 = � �
�  MNP, следовательно
MNP, следовательно  3 =
3 =  2,
2,
 3 =
3 =  5 (накрест лежащие при, MP‖MK, BT – cекущей),
5 (накрест лежащие при, MP‖MK, BT – cекущей),
-
 2 =
2 =  5 (соответственные при прямых NC и KB, NP – cекущей),
5 (соответственные при прямых NC и KB, NP – cекущей),
Если при пересечении двух прямых NC и KB, NP – cекущей, соответственные углы равны, то прямые NC‖KB.
Что и требовалось доказать.






































