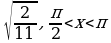Контрольно-измерительные материалы
по математике для промежуточной аттестации
учащихся 10 класса
Назначение КИМ – оценка уровня подготовки обучающихся 10 классов по математике.
Структура КИМ
Тестовая работа состоит из двух частей. Часть I включает 9 заданий базового уровня сложности: 7 заданий с выбором ответа по алгебре и началам анализа и 2 задания с кратким ответом по геометрии. Часть II включает 2 задания повышенного уровня сложности с развернутым ответом: одно по алгебре и одно по геометрии.
.Продолжительность работы
На выполнение работы отводится 40 минут
.Критерии оценивания отдельных заданий и работы в целом
Задания первой части оцениваются 1 баллом за правильный ответ и 0 баллов при неправильном ответе.
Максимальный балл за верно выполненное задание из второй части – 2 балла;
1 балл – ход решения верный, но отсутствует ответ на вопрос; или допущена одна ошибка вычислительного характера\описка, с её учетом решение доведено до конца.
Общий балл формируется путем суммирования баллов, полученных за выполнение первой и второй частей работы.
Менее 7 баллов - 2 (неудовлетворительно)
7-8 баллов - 3 (удовлетворительно)
9-10 баллов - 4 (хорошо)
11-13 баллов – 5 (отлично)
Работа составлена в 2-х вариантах
Вариант 1
А1. Упростите выражение 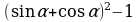
1) 0 3) sin2α
2) 1 4) cos2α
A2 Решите уравнение
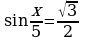
1) 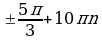 , n € Z 3)
, n € Z 3) 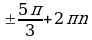 , n € Z
, n € Z
2) 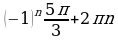 , n €Z 4)
, n €Z 4) 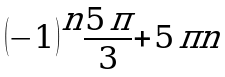 , n € Z
, n € Z
A3 Решите неравенство
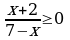
1) (-∞; - 6) 3) (- 1; 8)
 2) [-2; 7) 4) [0; +∞)
2) [-2; 7) 4) [0; +∞)
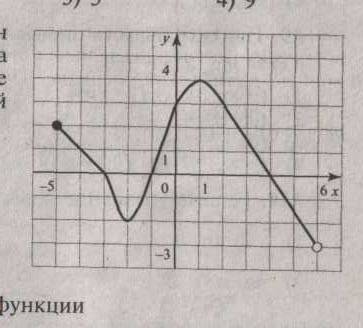
А4 На рисунке изображен график функции, заданной на промежутке 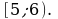 Укажите множество значений этой функции.
Укажите множество значений этой функции.
1) 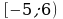
2) 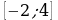
3) 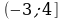
4) 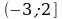
А5. Найдите множество значений функции 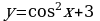
1) [0; 4] 3) [3; ∞)
2) [3; 4] 4) (3; 4)
А6. Найдите производную функции 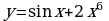
1) 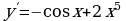 3)
3) 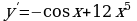
2) 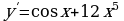 4)
4) 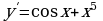
A7. Найдите угловой коэффициент касательной, проведенной к графику функции 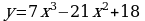 в его точке с абсциссой
в его точке с абсциссой 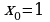
1) - 18 3) – 21
2) 22 4) 17
А8. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
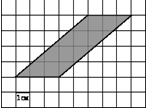
А9. В треугольнике ABC угол C равен 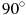 , ВС = 7, АС = 24 . Найдите sinА.
, ВС = 7, АС = 24 . Найдите sinА.
B1. Найдите значение выражения 1,5 – 3,4cosx, если sinx=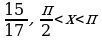
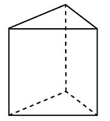
В2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Вариант 2
А1. Упростите выражение 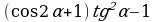
1) 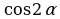 ; 3)
; 3) 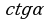 ;
;
2) 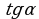 ; 4)
; 4) 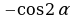 .
.
A2 Решите уравнение
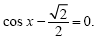
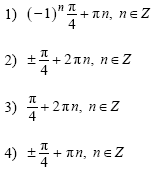
A3 Решите неравенство
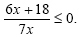
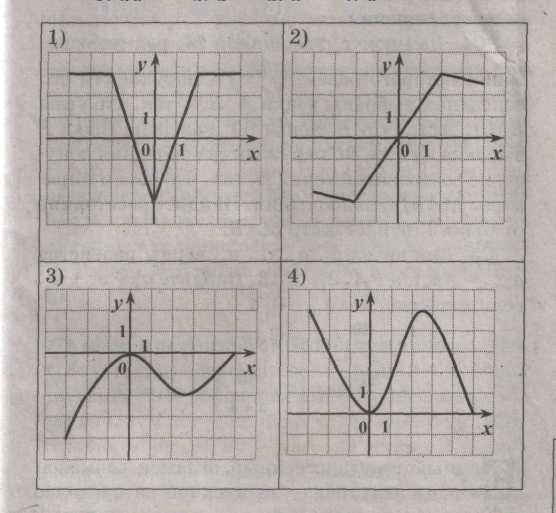 А4 На одном из рисунков изображен график четной функции. Укажите этот рисунок.
А4 На одном из рисунков изображен график четной функции. Укажите этот рисунок.
А5. Найдите множество значений функции 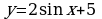
1) [-2; 2] 3) [-5; 5]
2) [3; 7 ] 4) [-1; 1]
А6. Найдите производную функции 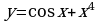 .
.
1) 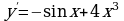 ; 2)
; 2) 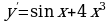 ;
;
3) 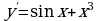 ; 4)
; 4) 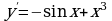 .
.
A7 . Найдите угловой коэффициент касательной, проведенной к графику функции 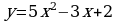 в его точке с абсциссой
в его точке с абсциссой 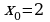 .
.
1) 16; 2) 17; 3) 0,3; 4) 0.
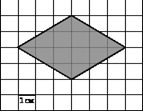
А8. На клетчатой бумаге с клетками размером 1 см × 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
А9. В треугольнике ABC угол C равен 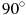 , AВ = 45, АС = 20 . Найдите tgА.
, AВ = 45, АС = 20 . Найдите tgА.
B1. Найдите значение выражения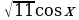 , если sinx=
, если sinx=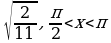
В2. Найдите площадь поверхности прямой призмы с боковым ребром, равным 5,в основании которой лежит ромб с диагоналями, равными 3 и 4.
ОТВЕТЫ
| 1вариант | номер задания | А1 | А2 | А3 | А4 | А5 |
|
| ответ | 3 | 4 | 2 | 3 | 2 |
|
| А6 | А7 | А8 | А9 | В1 | В2 |
|
| 2 | 3 | 12 | 0,28 | 3,1 | 10 |
| 2вариант | номер задания | А1 | А2 | А3 | А4 | А5 |
|
| ответ | 4 | 2 | 2 | 1 | 2 |
|
| А6 | А7 | А8 | А9 | В1 | В2 |
|
| 1 | 2 | 12 | √65\4 | - 3 | 62 |







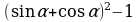
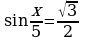
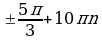 , n € Z 3)
, n € Z 3) 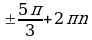 , n € Z
, n € Z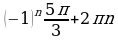 , n €Z 4)
, n €Z 4) 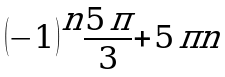 , n € Z
, n € Z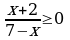
 2) [-2; 7) 4) [0; +∞)
2) [-2; 7) 4) [0; +∞)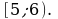 Укажите множество значений этой функции.
Укажите множество значений этой функции.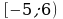
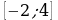
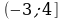
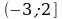
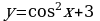
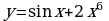
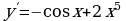 3)
3) 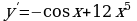
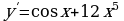 4)
4) 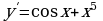
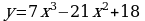 в его точке с абсциссой
в его точке с абсциссой 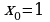

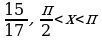

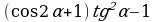
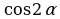 ; 3)
; 3) 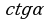 ;
;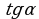 ; 4)
; 4) 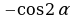 .
.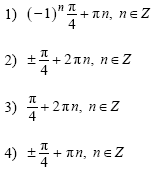
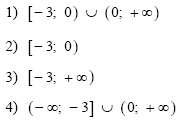
 А4 На одном из рисунков изображен график четной функции. Укажите этот рисунок.
А4 На одном из рисунков изображен график четной функции. Укажите этот рисунок.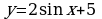
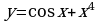 .
.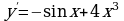 ; 2)
; 2) 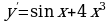 ;
; 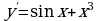 ; 4)
; 4) 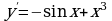 .
.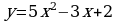 в его точке с абсциссой
в его точке с абсциссой 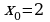 .
.
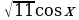 , если sinx=
, если sinx=