Контрольная работа
«Четырехугольники»
Вариант 1
1. В прямоугольнике АВСD диагонали АС и BD пересекаются в точке О. Угол АВО = 400. Найти углы между диагоналями прямоугольника (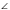 АОВ и
АОВ и 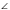 ВОС)
ВОС)
2. Биссектриса ВМ параллелограмма АВСD делит сторону АD на отрезки АМ = 4,5 см и МD = 2,5 см. Докажите, что ∆ АВМ равнобедренный и найдите стороны параллелограмма.
3. В ромбе АВСD диагонали пересекаются в точке О. На диагонали АС отложены отрезки ОМ и ОN , равные ВО. Определите вид четырехугольника ВМDN.
Вариант 2
1. В ромбе АВСD диагонали АС и BD пересекаются в точке О. Угол АDС = 1080. Найти углы треугольника ∆АОВ (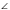 ВАО,
ВАО, 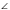 АВО,
АВО, 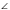 АОВ)
АОВ)
2. Биссектриса ВЕ параллелограмма АВСD пересекает сторону АD в точке Е. 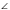 АЕВ = 620. Докажите, что ∆ АВЕ равнобедренный и найдите углы параллелограмма.
АЕВ = 620. Докажите, что ∆ АВЕ равнобедренный и найдите углы параллелограмма.
3. В прямоугольнике АВСD на сторонах ВС и АD отмечены точки Е и F так, что АВ = ВЕ и СD = FD. Определите вид четырехугольника АЕCF.
Контрольная работа
«Площадь»
Вариант 1
1. Найти высоту треугольника, если сторона, к которой эта высота проведена, равна 5 см, а площадь треугольника – 10 см2.
2. Площадь квадрата равна 144 см2. Найти его сторону.
3. Диагонали ромба равны 6 см и 8 м. Чему равна его площадь?
4. В равнобокой трапеции АВСD основания АD и ВС равны соответственно 16 см и 6 см. Высота ВМ трапеции равна 8 см. Из вершины тупого угла С проведен перпендикуляр СК на основание АD. Установить соответствие между задаными фигурами (1-4) та их площадями (А-Д):
| 1) | трапеция АВСD; | А) | 68 см2; |
| 2) | ∆АВМ; | Б) | 20 см2; |
| 3) | четырёхугольник ВСDМ; | В) | 88 см2; |
| 4) | четырёхугольник МВСК. | Г) | 40 см2; |
|
|
| Д) | 48 см2. |
5. Площадь параллелограмма 96 дм2, периметр 44 дм, а расстояние между большими сторонами 8 дм. Найдите расстояние между меньшими сторонами параллелограмма.
6. Перпендикуляр, опущенный из вершины прямоугольника делит его диагональ на отрезки 36 см и 64 см. Вычислить площадь прямоугольника.
Вариант 2
1. Найти сторону треугольника, если высота, проведенная к этой стороне, равна 6 см, а площадь треугольника – 12 см2.
2. Сторона квадрата равна 15 см. Найти его площадь.
3. Диагонали ромба равны 7 см и 8 м. Чему равна его площадь?
4. В прямоугольной трапеции АВСD основания АD и ВС равны соответственно 14 см и10 см. Боковое ребро трапеции, перпендикулярное её основаниям, равно 5 см. Из вершины тупого угла С проведен перпендикуляр СК на основание АD. Установить соответствие между задаными фигурами (1-4) та их площадями (А-Д):
| 1) | трапеция АВСD; | А) | 60 см2; |
| 2) | ∆АВК; | Б) | 12 см2; |
| 3) | четырёхугольник КВСD; | В) | 35 см2; |
| 4) | четырёхугольник АВСК. | Г) | 25 см2; |
|
|
| Д) | 50 см2. |
5. Площадь параллелограмма 60 дм2, периметр 70 дм, а расстояние между меньшими сторонами 4 дм. Найдите расстояние между большими сторонами параллелограмма.
6. Перпендикуляр, опущенный из вершины прямоугольника делит его диагональ на отрезки 9 см и 16 см. Вычислить площадь прямоугольника.
Контрольная работа
«Теорема Пифагора»
Вариант 1
1. Диагонали ромба равны 16см и 30см. Найдите периметр ромба.
2. В равнобедренном треугольнике АВС (основание АС) боковая сторона равна 17см, а высота АК равна 8см. Найдите основание.
3. В прямоугольной трапеции боковые стороны 12см и 13см, а большая диагональ 15см. Найдите основания трапеции.
4. В прямоугольном треугольнике с острым углом 45° гипотенуза равна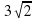 см. найдите катеты и площадь этого треугольника.
см. найдите катеты и площадь этого треугольника.
5. Катет прямоугольного треугольника равен 8см, а медиана, проведённая к этому катету, равна 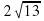 см. Найдите гипотенузу треугольника.
см. Найдите гипотенузу треугольника.
Вариант 2
1. Диагонали ромба равны 18см и 80см. Найдите периметр ромба.
2. В равнобедренном треугольнике АВС (основание АС) боковая сторона равна 25см, а высота СК равна 24см. Найдите основание.
3. В прямоугольной трапеции боковые стороны 12см и 20см, а меньшая диагональ 13см. Найдите основания трапеции.
4. В прямоугольном треугольнике катет, лежащий против угла 60°, равен 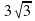 см. Найдите две другие стороны этого треугольника и его площадь.
см. Найдите две другие стороны этого треугольника и его площадь.
5. Катет прямоугольного треугольника равен 8см, а медиана, проведённая к другому катету, равна 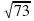 см. Найдите гипотенузу треугольника.
см. Найдите гипотенузу треугольника.
Контрольная работа
«Подобные треугольники. Признаки подобия»
Вариант 1
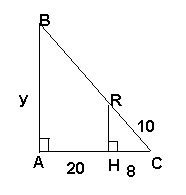
∠АСВ=∠СКМ. Найти х 2) Найти FK.
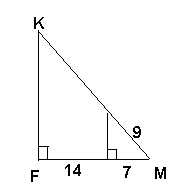
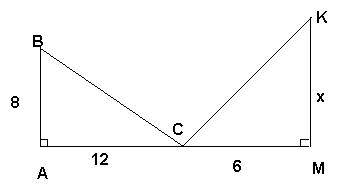
Найти у.
Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АВ, если ОВ=4 см, ОД=10 см, ДС=25 см.
* Докажите, что два равносторонних треугольника подобны.
Вариант 2
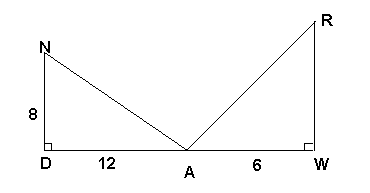
∠DAN=∠ARW. Найти RW 2) найти у
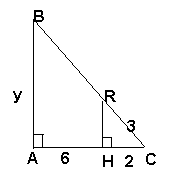
3) Найти FK.

Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АО, если АВ=9,6 дм, ДС=24 см, АС=15 см.
5) * Докажите, что два равносторонних треугольника подобны.
Контрольная работа
«Применение подобия»
Вариант 1
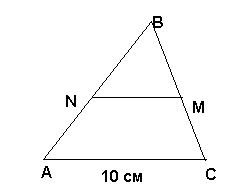
Найти среднюю линий NM треугольника АВС.
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Длина тени дерева равна 10 м, а длина тени человека, рост которого 1,8 м равна 3 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
Вариант 2
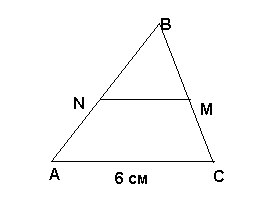
Найти среднюю линий NM треугольника АВС.
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.
Длина тени дерева равна 12 м, а длина тени человека, рост которого 1,6 м равна 2,5 м. Найти высоту дерева.
Постройте треугольник АВС по двум углам и высоте, проведенной из вершины третьего угла.
Постройте прямоугольный треугольник по гипотенузе и отношению катетов.
Контрольная работа
«Окружность»
Вариант 1
Радиус окружности равен 10 см, а расстояние от одного конца диаметра до точки окружности равно 16 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С - точки касания). Найдите периметр треугольника АВС, если ОА=12 см, а угол ВОС=600.
Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см. Найти площадь этого треугольника.
Вариант 2
Радиус окружности равен 5 см, а расстояние от одного конца диаметра до точки окружности равно 10 см. Найдите расстояние от другого конца диаметра до этой точки.
Из точки А к окружности с центром О проведены касательные АВ и АС (В и С - точки касания). Найдите периметр треугольника АВС, если ОА=10 см, а угол ВОС=600.
Из точки А к окружности с центром О проведена касательная АВ. Найдите АО, если радиус окружности 12, а угол АОВ=450.
Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.
Итоговая контрольная работа
Вариант 1
1. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.
2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.
3. В равнобедренной трапеции боковая сторона равна 13 см, основания 10 см и 20 см. Найдите площадь трапеции.
4. В треугольнике АВС прямая MN , параллельная стороне АС, делит сторону ВС на отрезки BN=15 см и NC=5 см, а сторону АВ на ВМ и АМ. Найдите длину отрезка MN, если АС=15 см.
5. Дан прямоугольный треугольник АВС, у которого 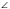 С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и 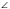 А=60°. Найдите:
А=60°. Найдите:
а) остальные стороны ∆АВС
б) площадь ∆АВС
в) длину высоты, опущенной из вершины С.
Вариант 2
1. В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.
2. В параллелограмме АВСД АВ=8 см, АД=10 см, 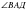 =30°. Найдите площадь параллелограмма.
=30°. Найдите площадь параллелограмма.
3. В прямоугольной трапеции АВСД боковая сторона равна АВ=10 см, большее основание АД= 18 см, 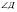 =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.
4. В треугольнике АВС со сторонами АС=12 см и АВ=18 см проведена прямая MN, параллельная АС, MN=9 см. Найдите ВМ.
5. Дан прямоугольный треугольник АDС, у которого 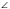 D-прямой, катет AD=3 см и
D-прямой, катет AD=3 см и 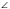 DАC=30°. Найдите:
DАC=30°. Найдите:
а) остальные стороны ∆АDС
б) площадь ∆АDС
в) длину высоты, проведенной к гипотенузе.







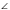 АОВ и
АОВ и 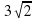 см. найдите катеты и площадь этого треугольника.
см. найдите катеты и площадь этого треугольника.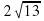 см. Найдите гипотенузу треугольника.
см. Найдите гипотенузу треугольника.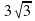 см. Найдите две другие стороны этого треугольника и его площадь.
см. Найдите две другие стороны этого треугольника и его площадь.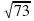 см. Найдите гипотенузу треугольника.
см. Найдите гипотенузу треугольника.






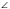 С-прямой, катет ВС=6 см и
С-прямой, катет ВС=6 см и 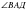 =30°. Найдите площадь параллелограмма.
=30°. Найдите площадь параллелограмма.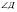 =45°. Найдите площадь трапеции.
=45°. Найдите площадь трапеции.


















