Контрольная работа №1 «Четырёхугольники»
Вариант I
1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если  АВО = 30°.
АВО = 30°.
2. В параллелограмме KМNP проведена биссектриса угла МKР, которая пересекает сторону MN в точке Е.
а) Докажите, что треугольник KМЕ равнобедренный.
б) Найдите сторону KР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.
Вариант II
1. Диагонали ромба KМNP пересекаются в точке О. Найдите углы треугольника KОМ, если угол МNP равен 80°.
2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ = ВМ.
а) Докажите, что АМ – биссектриса угла ВАD.
б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см.
Вариант III
1. Через вершину С прямоугольника АВСD проведена прямая, параллельная диагонали ВD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника АСМN, если диагональ ВD равна 8 см.
2. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Луч DМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСD, если АN = 10 см.
Контрольная работа № 2 «Площадь».
Вариант I
1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.
2. Площадь прямоугольной трапеции равна 120 см2, а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.
Вариант II
1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см2.
2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см,  В = 150°.
В = 150°.
3. На продолжении стороны KN данного треугольника KМN постройте точку Р так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KМN.
Вариант III
(для более подготовленных учащихся)
1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 30°. Найдите площадь параллелограмма.
2. Середина М боковой стороны CD трапеции АВСD соединена отрезками с вершинами А и В. Докажите, что площадь треугольника АВМ в два раза меньше площади данной трапеции.
3. Точки А1, В1, С1 лежат соответственно на сторонах ВС, АС, АВ треугольника АВС, причем АВ1 =  AC, CA1 =
AC, CA1 =  CB, BC1 =
CB, BC1 =  BA. Найдите площадь треугольника А1В1С1, если площадь треугольника АВС равна 27 см2.
BA. Найдите площадь треугольника А1В1С1, если площадь треугольника АВС равна 27 см2.
Контрольная работа №3 «Подобие треугольников»
Вариант I
1. На рисунке 1 АВ || СD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.

Рис. 1
2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, KM = 10 cм, MN = 15 см, NK = 20 см.
Вариант II
1. На рисунке 2 MN || АС. а) Докажите, что АВ · BN = CВ · BM. б) Найдите MN, если AM = 6 см, ВM = 8 см, АС = 21 см.

Рис. 2
2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 cм, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.
Контрольная работа №4 «Решение прямоугольных треугольников»
| ВАРИАНТ 1 1. Закончить предложение: а) косинусом острого угла прямоугольного треугольника называется… б) тангенсом острого угла прямоугольного треугольника называется… 2. В треугольнике АВС С=90о , АС=6см, ВС=8см. Найдите 1)tgB; 2) sinА. 3. Найдите катет АС прямоугольного треугольника АВС, если его гипотенуза АВ=7см, а А=45о. 4. Постройте угол косинус которого равен  . . 5. В прямоугольном треугольнике гипотенуза равна 8см, а один из острых углов 50о. Решите треугольник. 6. В прямоугольном треугольнике гипотенуза больше одного из катетов на 2см, а второй катет равен 4 см. Найдите тангенс острого угла, лежащего против большего катета. см. Найдите тангенс острого угла, лежащего против большего катета. | ВАРИАНТ 2 1. Закончить предложение: а) синусом острого угла прямоугольного треугольника называется… б) котангесом острого угла прямоугольного треугольника называется… 2. В треугольнике АВС С=90о , АС=3см, ВС=4см. Найдите 1) сtgB; 2) cosА. 3. Найдите гипотенузу АВ прямоугольного треугольника АВС, если его катет АС=7см, а А=45о. 4. Постройте угол тангенс которого равен 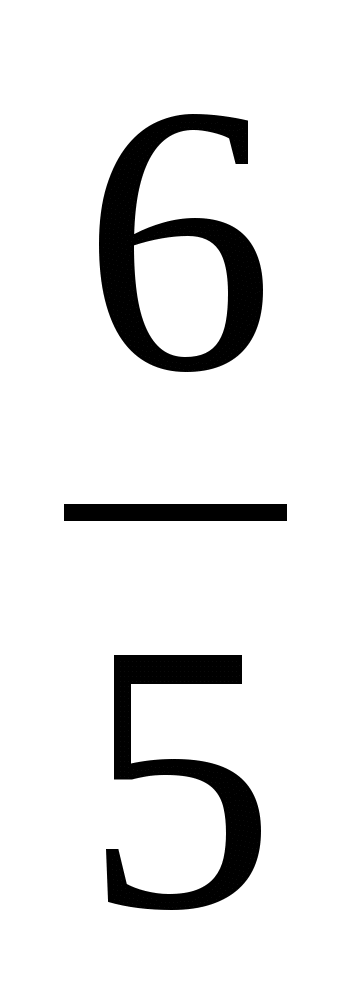 . . 5. В прямоугольном треугольнике гипотенуза равна 6см, а один из острых углов 35о.Решите треугольник. 6. В прямоугольном треугольнике один катет больше второго катета на 1см, а гипотенуза равна 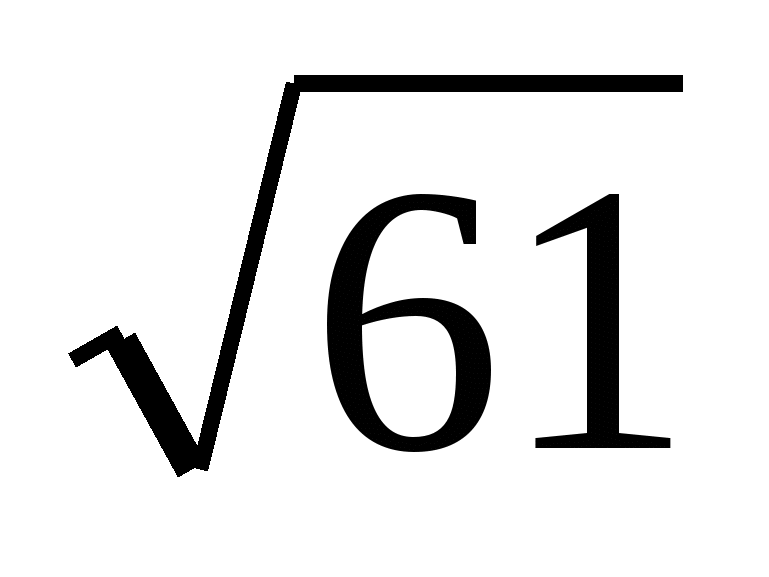 см. Найдите тангенс острого угла, лежащего против меньшего катета. см. Найдите тангенс острого угла, лежащего против меньшего катета. |
| ВАРИАНТ 1 1. Закончить предложение: а) косинусом острого угла прямоугольного треугольника называется… б) тангенсом острого угла прямоугольного треугольника называется… 2. В треугольнике АВС С=90о , АС=6см, ВС=8см. Найдите 1)tgB; 2) sinА. 3. Найдите катет АС прямоугольного треугольника АВС, если его гипотенуза АВ=7см, а А=45о. 4. Постройте угол косинус которого равен  . . 5. В прямоугольном треугольнике гипотенуза равна 8см, а один из острых углов 50о. Решите треугольник. 6. В прямоугольном треугольнике гипотенуза больше одного из катетов на 2см, а второй катет равен 4 см. Найдите тангенс острого угла, лежащего против большего катета. см. Найдите тангенс острого угла, лежащего против большего катета. | ВАРИАНТ 2 1. Закончить предложение: а) синусом острого угла прямоугольного треугольника называется… б) котангесом острого угла прямоугольного треугольника называется… 2. В треугольнике АВС С=90о , АС=3см, ВС=4см. Найдите 1) сtgB; 2) cosА. 3. Найдите гипотенузу АВ прямоугольного треугольника АВС, если его катет АС=7см, а А=45о. 4. Постройте угол тангенс которого равен 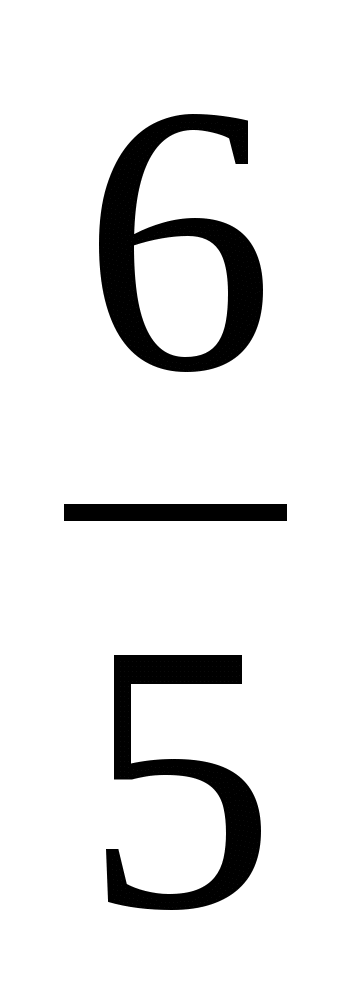 . . 5. В прямоугольном треугольнике гипотенуза равна 6см, а один из острых углов 35о.Решите треугольник. 6. В прямоугольном треугольнике один катет больше второго катета на 1см, а гипотенуза равна 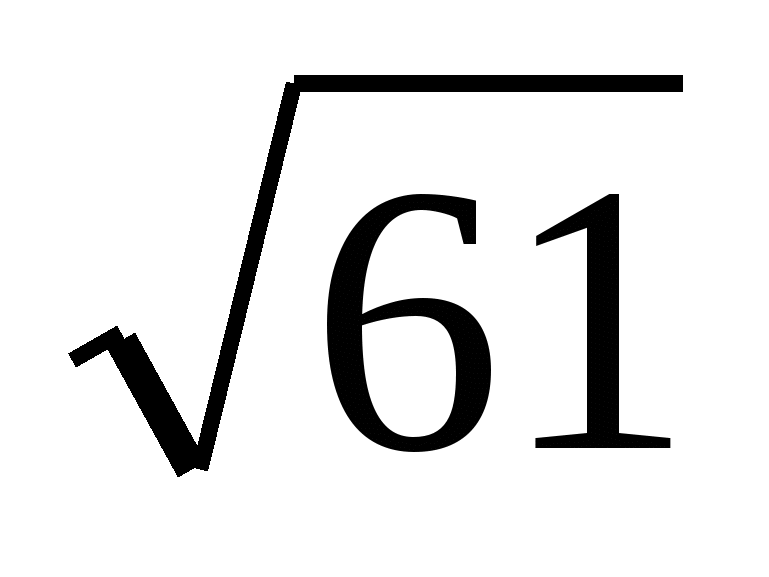 см. Найдите тангенс острого угла, лежащего против меньшего катета. см. Найдите тангенс острого угла, лежащего против меньшего катета. |
Контрольная работа № 5 «Окружность».
Вариант I
1. Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.
Вариант II
1. Отрезок ВD – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.
2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.



























