Контрольная работа № 1 по теме "Аксиомы стереометрии и следствия из них. Начальные представления о многогранниках" (10 класс, Мерзляк А.Г. и др.)

Контрольная работа № 1 по теме «Аксиомы стереометрии и следствия из них. Начальные представления о многогранниках»

В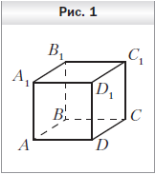 ариант 1

1. На рисунке 1 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей A₁DC и BB₁C₁.

2. Даны точки A, B и C такие, что AB = 12 см, BC = 19 см,
AC = 7 см. Сколько плоскостей можно провести через точки A, B и C? Ответ обоснуйте.

3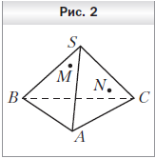 . Плоскость α проходит через вершины A и D параллелограмма ABCD и точку O пересечения его диагоналей. Докажите, что прямая BC лежит в плоскости α.

4. Точки M и N принадлежат соответственно граням SAB и SAC пирамиды SABC (рис. 2). Постройте точку пересечения прямой MN с плоскостью ABC.

5. Постройте сечение пирамиды SABC плоскостью, проходящей через точки D, E и F, принадлежащие соответственно рёбрам AB, BC и SC, причём прямые DE и AC не параллельны.

В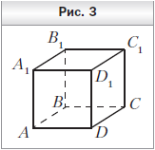 ариант 2

1. На рисунке 3 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей A₁BC и ABB₁.

2. Даны точки M, N и K такие, что MN = 23 см, MK = 14 см,
NK = 13 см. Сколько плоскостей можно провести через точки M, N и K? Ответ обоснуйте.

3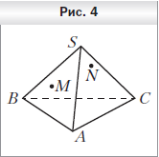 . Точки D и E — середины сторон AB и BC треугольника ABC соответственно. Плоскость α проходит через точки B, D и E. Докажите, что прямая AC лежит в плоскости α.

4. Точки M и N принадлежат соответственно граням SAB и SBC пирамиды SABC (рис. 4). Постройте точку пересечения прямой MN с плоскостью ABC.

5. Постройте сечение призмы ABCA₁B₁C₁ плоскостью, проходящей через точки M, K и N, принадлежащие соответственно рёбрам AB, BC и CC₁, причём прямые MK и AC не параллельны.

В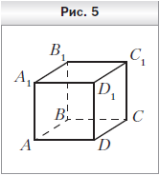 ариант 3

1. На рисунке 5 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей AD₁C₁ и B₁BC .

2. Даны точки D, E и F такие, что DE = 11 см, EF = 16 см,
DF = 27 см. Сколько плоскостей можно провести через точки D, E и F? Ответ обоснуйте.

3. В окружности с центром O проведены диаметры AB и CD. Плоскость α проходит через точки A, C и O. Докажите, что прямая BD лежит в плоскости α.

4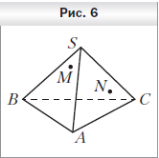 . Точки M и N принадлежат соответственно граням SBC и SAC пирамиды SABC (рис. 6). Постройте точку пересечения прямой MN с плоскостью ABC.

5. Постройте сечение пирамиды SABC плоскостью, проходящей через точки M, K и N, принадлежащие соответственно рёбрам SA, SB и BC, причём прямые MK и AB не параллельны.

Вариант 4

1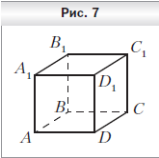 . На рисунке 7 изображён куб ABCDA₁B₁C₁D₁. Укажите прямую пересечения плоскостей D₁BC и AA₁B₁.

2. Даны точки B, C и D такие, что BC = 4 см, CD = 16 см, BD = 18 см. Сколько плоскостей можно провести через точки B, C и D? Ответ обоснуйте.

3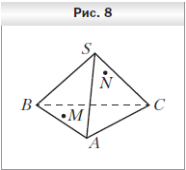 . Отрезок AD — биссектриса треугольника ABC, точка O — центр окружности, вписанной в треугольник ABC. Плоскость α проходит через точки A, O и C. Докажите, что точка B лежит в плоскости α.

4. Точки M и N принадлежат соответственно граням SAB и SBC пирамиды SABC (рис. 8). Постройте точку пересечения прямой MN с плоскостью SAC.

5. Постройте сечение куба ABCDA₁B₁C₁D₁ плоскостью, проходящей через вершину B₁ и точки M и K, принадлежащие соответственно рёбрам AB и CC₁.