Контрольная работа № 2 по теме "Параллельность в пространстве" (10 класс, Мерзляк А.Г. и др.)

Контрольная работа № 2 по теме «Параллельность в пространстве»

Вариант 1

1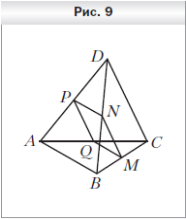 . Точки M, N, P и Q — середины отрезков BC, BD, AD и AC соответственно, AB = 14 см, CD = 18 см (рис. 9). Определите вид четырёхугольника MNPQ и вычислите его периметр.

2. Плоскость α пересекает стороны AB и BC треугольника ABC в точках M и K соответственно и параллельна стороне AC, MK = 4 см, MB : MA = 2 : 3. Найдите сторону AC треугольника.

3 . Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 10). Постройте изображение высоты треугольника, опущенной на сторону A₁C₁.

4. Плоскости α и β параллельны. Из точки M, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках A₁ и B₁, а другой — в точках A₂ и B₂ соответственно. Найдите отрезок B₁B₂ , если он на 2 см больше отрезка A₁A₂ , MB₁ = 7 см, A₁B₁ = 4 см.

5. Точки A, B, C, не лежащие на одной прямой, являются параллельными проекциями трёх последовательных вершин правильного шестиугольника. Постройте изображение этого шестиугольника.

Вариант 2

1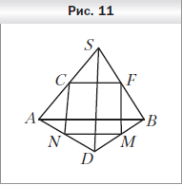 . Точки F, M, N и C — середины отрезков BS, DB, AD и AS соответственно, SD = 30 см, AB = 36 см (рис. 11). Определите вид четырёхугольника FMNC и вычислите его периметр.

2. Плоскость β пересекает стороны AB и AC треугольника ABC в точках N и D соответственно и параллельна стороне BC, AD = 6 см, DN : CB = 3 : 4. Найдите сторону AC треугольника.

3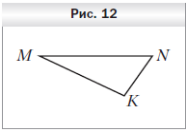 . Треугольник MNK является изображением правильного треугольника M₁N₁K₁ (рис. 12). Постройте изображение биссектрисы треугольника, проведённой из вершины M₁.

4. Плоскости α и β параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках A₁ и B₁, а другая — в точках A₂ и B₂ соответственно. Найдите отрезок A₁A₂ , если он на 1 см меньше отрезка B₁B₂ , MA₂ = 4 см, A₂B₂ = 10 см.

5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин квадрата и его центра. Постройте изображение квадрата.

Вариант 3

1 . Точки N, M, C и K — середины отрезков BD, DF, FA и AB соответственно, BF = 24 см, AD = 18 см (рис. 13). Определите вид четырёхугольника NMCK и вычислите его периметр.

2. Плоскость α пересекает стороны MF и MK треугольника MFK в точках A и B соответственно и параллельна стороне FK,
AB = 12 см, AM : AF = 3 : 5. Найдите сторону FK треугольника.

3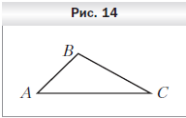 . Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 14). Постройте изображение центра вписанной окружности треугольника A₁B₁C₁.

4. Плоскости α и β параллельны. Из точки O, не принадлежащей этим плоскостям и не находящейся между ними, проведены два луча. Один из них пересекает плоскости α и β в точках C₁ и D₁, а другой — в точках C₂ и D₂ соответственно. Найдите отрезок C₁C₂, если он на 5 см меньше отрезка D₁D₂, OC₁ = 4 см,
C₁D₁ = 10 см.

5. Точки A, B и O, не лежащие на одной прямой, являются соответственно параллельными проекциями двух вершин правильного треугольника и его центра. Постройте изображение этого треугольника.

В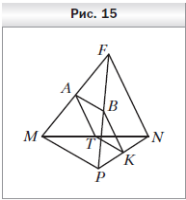 ариант 4

1. Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см (рис. 9). Определите вид четырёхугольника ABKT и вычислите его периметр.

2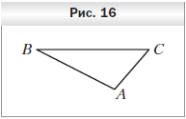 . Плоскость β пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.

3. Треугольник ABC является изображением правильного треугольника A₁B₁C₁ (рис. 16). Постройте изображение центра описанной окружности треугольника A₁B₁C₁.

4. Плоскости α и β параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках M₁ и N₁, а другая — в точках M₂ и N₂ соответственно. Найдите отрезок M₁M₂ , если он на 8 см больше отрезка N₁N₂ , N₁M₁= 30 см, DN₁ = 5 см.

5. Точки A, B и M, не лежащие на одной прямой, являются соответственно параллельными проекциями двух соседних вершин параллелограмма и середины его противолежащей стороны. Постройте изображение этого параллелограмма.