Контрольная работа по геометрии №2
на тему «Преобразование подобия. Метрические соотношения в окружности»
Вариант 1
 Задача 1.
Задача 1.
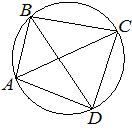
Четырёхугольник ABCD вписан в окружность.
Угол ABD равен 51°, угол CAD равен 42°.
Найдите угол ABC. Ответ дайте в градусах.
Задача 2.
| На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=68°. Найдите угол NMB. Ответ дайте в градусах. | 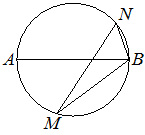
|
 Задача 3.
Задача 3.
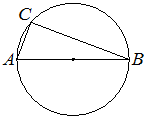
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 6,5. Найдите AC, если BC=12.
Задача 4.
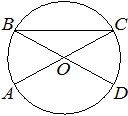 В окружности с центром в точке O отрезки AC и BD - диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром в точке O отрезки AC и BD - диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.
Задача 5.
| Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах. | 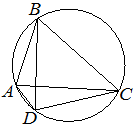
|
Задача 6.
| Отрезки AC и BD - диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах. | 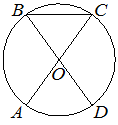
|
Задача 7.
Хорды АВ и CD окружности пересекаются в точке Е. Найти ЕD, если АЕ=3, ВЕ=4, СЕ=2
Задача 8.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.
 Задача 9.
Задача 9.
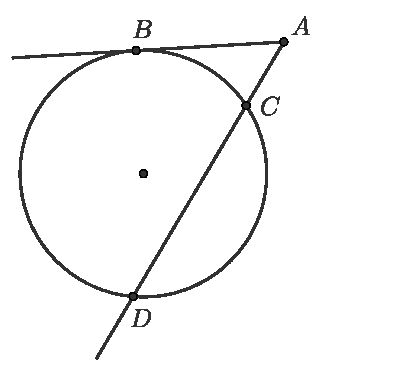
Из точки А вне окружности проведена касательная АВ и секущая AD, как показано на картинке. Найдите длину отрезка АС, если СD=5, а длина отрезка касательной равна 6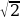 .
.
Задача 10.
Точки М и Р лежат соответственно на сторонах ВС и АВ треугольника АВС, причем МР II АС. Найти сторону АВ, если АС=12см, МР=4см, РВ=5см?
Контрольная работа по геометрии №2
на тему «Преобразование подобия. Метрические соотношения в окружности»
Вариант 2
Задача 1.
| Четырёхугольник ABCD вписан в окружность. Угол ABD равен 80°, угол CAD равен 34°. Найдите угол ABC. Ответ дайте в градусах. | 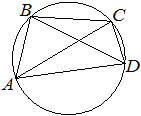
|
Задача 2.
| 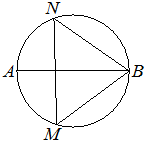 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=34°. Найдите угол NMB. Ответ дайте в градусах. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=34°. Найдите угол NMB. Ответ дайте в градусах.
|
|
Задача 3.
| Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 8,5. Найдите BC, если AC=8. | 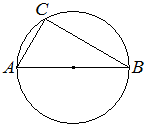
|
 Задача 4.
Задача 4.
В окружности с центром в точке O отрезки AC и BD - диаметры. Угол AOD равен 148°. Найдите угол ACB. Ответ дайте в градусах.
Задача 5.
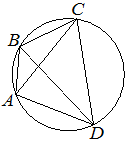
| Четырёхугольник ABCD вписан в окружность. Угол ABC равен 132°, угол CAD равен 80°. Найдите угол ABD. Ответ дайте в градусах.
| 
|
Задача 6.
| Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 115°. Ответ дайте в градусах. | 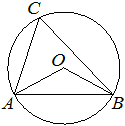
|
Задача 7.
Хорды АС и ВD окружности пересекаются в точке Р. Найти АР, если ВР=15, СР=6, DР=10
Задача 8.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём, AB=3, AC=12. . Найдите AK
Задача 9.
Точки В, С, D и E угла CAE лежат на окружности, причём точка B лежит на AC. AB=3, AC=6, AD=2. Найдите DE.
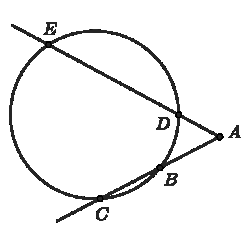
Задача 10.
Точки К и Н лежат соответственно на сторонах АС и СВ треугольника АВС, причем МР II АВ. Найти сторону АС, если КС=12см, КН=6см, АВ=8см?
Контрольная работа по геометрии №2
на тему «Преобразование подобия. Метрические соотношения в окружности»
Вариант 3
Задача 1.
| Четырёхугольник ABCD вписан в окружность. Угол ABD равен 85°, угол CAD равен 19°. Найдите угол ABC. Ответ дайте в градусах. | 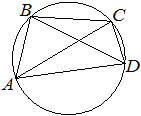
|
|
Задача2.
| На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах. | 
|
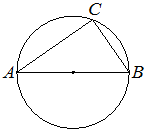 Задача 3.
Задача 3.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.
 Задача 4.
Задача 4.
Отрезки AC и BD —— диаметры окружности с центром в точке O. Угол ACB равен 23°. Найдите угол AOD. Ответ дайте в градусах.

Задача 5.
| Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах. |
|
Задача 6.
| Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 67°. Ответ дайте в градусах. | 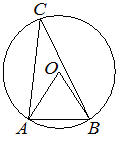
|
Задача 7.
Хорды AC и BD окружности пересекаются в точке P. BP =4, CP=12, DP =21. Найдите AP
Задача 8.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём , AB = 6, AC = 54. Найдите AK
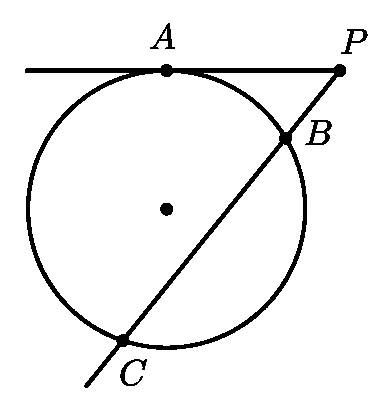
Задача 9.
Луч РА касается окружности в точке А, а луч РС пересекает эту окружность в точках В и С. При этом РА=4, РС=8. Найдите РВ.
Задача 10.
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 6, AC = 24.
Контрольная работа по геометрии №2
на тему «Преобразование подобия. Метрические соотношения в окружности»
Вариант 4
 Задача 1.
Задача 1.
| Четырёхугольник ABCD вписан в окружность. Угол ABD равен 38°, угол CAD равен 54°. Найдите угол ABC. Ответ дайте в градусах. |
|
Задача 2.
| На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах. | 
|
Задача 3.
| Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 25. Найдите AC, если BC=48. | 
|
Задача 4.
| В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 86°. Найдите угол ACB. Ответ дайте в градусах. | 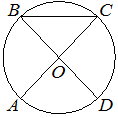
|
Задача 5.
|
|
|
| Четырёхугольник ABCD вписан в окружность. Угол ABC равен 54°, угол CAD равен 41°. Найдите угол ABD. Ответ дайте в градусах. | 
|
Задача 6.
| Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 153°. Ответ дайте в градусах. | 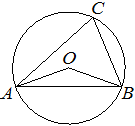
|
Задача 7.
Хорды AC и BD окружности пересекаются в точке P. Найдите AP, если BP =12, CP =15, DP = 25
Задача 8.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём , AB =5, AC = 45. Найдите AK
 Задача 9.
Задача 9.
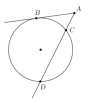
Из точки А вне окружности проведена касательная АВ и секущая AD, как показано на картинке. Найдите длину отрезка СD, если АС=5, а длина отрезка касательной равна 10.
Задача 10.
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH = 8, AC = 32.







 Задача 1.
Задача 1.
 Задача 3.
Задача 3. В окружности с центром в точке O отрезки AC и BD - диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром в точке O отрезки AC и BD - диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах. 

 Задача 9.
Задача 9.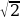 .
.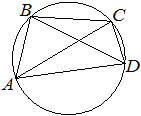
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=34°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=34°. Найдите угол NMB. Ответ дайте в градусах.



 Задача 3.
Задача 3.



 Задача 9.
Задача 9.

















