Контрольная работа № 2 по теме «Цилиндр. Конус. Усечённый конус. Комбинации цилиндра, конуса и усечённого конуса с многогранниками»
Вариант 1
1. Радиус основания цилиндра равен 6 см, а высота – 5 см. Найдите диагональ осевого сечения цилиндра.
2. Найдите высоту конуса, диаметр основания которого равен 10 см, а образующая наклонена к плоскости основания под углом 30°.
3. Радиусы оснований усечённого конуса равны 9 см и 17 см, а высота – 15 см. Найдите образующую усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение, диагональ которого образует с плоскостью основания угол 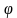 . Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R.
. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R.
5. Сторона основания правильной четырёхугольной призмы равна 8 см, а диагональ боковой грани образует с плоскостью основания угол 60°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – треугольник, одна из сторон которого равна c, а противолежащий ей угол равен γ. Все боковые рёбра пирамиды наклонены к плоскости основания под углом α. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 2
1. Диагональ осевого сечения цилиндра равна 10 см, а высота цилиндра – 8 см. Найдите радиус основания цилиндра.
2. Найдите диаметр основания конуса, высота которого равна 12 см, а образующая наклонена к плоскости основания под углом 60°.
3. Радиусы оснований усечённого конуса равны 14 см и 10 см, а образующая –
5 см. Найдите высоту усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение, которое пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α,
0° d и образует с плоскостью основания угол β.
5. Сторона основания правильной треугольной призмы равна 18 см, а диагональ боковой грани образует с плоскостью основания угол 45°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды — прямоугольный треугольник, катет которого равен b, а противолежащий острый угол равен β. Все боковые рёбра пирамиды наклонены к плоскости основания под углом α. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 3
1. Радиус основания цилиндра равен 6 см, а диагональ осевого сечения – 13 см. Найдите высоту цилиндра.
2. Найдите образующую конуса, если она наклонена к плоскости основания под углом 45°, а высота конуса равна 18 см.
3. Радиус меньшего основания усечённого конуса равен 8 см, образующая – 15 см, а высота – 9 см. Найдите радиус большего основания усечённого конуса.
4. Радиус основания цилиндра равен R. Параллельно оси цилиндра проведено сечение. Хорда нижнего основания, принадлежащая сечению, видна из центра этого основания под углом 2α. Отрезок, соединяющей центр верхнего основания цилиндра с точкой окружности нижнего основания, образует с плоскостью основания угол β. Найдите площадь сечения.
5. Высота правильной четырёхугольной призмы равна 6 см, а диагональ боковой грани образует с плоскостью основания угол 60°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – прямоугольник, одна из сторон которого равна a и образует с диагональю прямоугольника угол α. Все боковые рёбра пирамиды наклонены к плоскости основания под углом β. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
Вариант 4
1. Радиус основания цилиндра равен 5 см, а высота – 2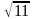 см. Найдите диагональ осевого сечения цилиндра.
см. Найдите диагональ осевого сечения цилиндра.
2. Найдите радиус основания конуса, образующая которого равна 14 см и наклонена к плоскости основания под углом 60°.
3. Радиус большего основания усечённого конуса равен 11 см, образующая – 13 см, а высота – 12 см. Найдите радиус меньшего основания усечённого конуса.
4. В цилиндре параллельно его оси проведено сечение. Диагональ сечения наклонена к плоскости основания под углом β. Хорда нижнего основания, принадлежащая сечению, видна из центра этого основания под углом α и удалена от него на расстояние, равное d. Найдите площадь сечения.
5. Высота правильной треугольной призмы равна 12 см, а диагональ боковой грани образует с плоскостью основания угол 30°. Найдите площадь боковой поверхности цилиндра, вписанного в данную призму.
6. Основание пирамиды – равнобедренный треугольник с боковой стороной a и углом β при вершине. Все боковые рёбра пирамиды наклонены к плоскости основания под углом 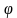 . Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.
. Найдите площадь боковой поверхности конуса, описанного около данной пирамиды.







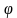 . Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R.
. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° R. 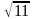 см. Найдите диагональ осевого сечения цилиндра.
см. Найдите диагональ осевого сечения цилиндра. 









