Задания для итогового контроля
1. Общие положения
Формой аттестации по дисциплине является контрольная работа. Итогом работы является оценка знаний и умений обучающегося по пятибалльной шкале.
Контрольная работа проводится в форме выполнения заданий.
Условия проведения
Количество вариантов задания - 4.
Задания предусматривают одновременную проверку усвоенных знаний и освоенных умений по всем темам программы. Ответы предоставляются письменно.
Время выполнения задания - 2 часа (академических).
Оборудование: бумага, ручка, карандаш, линейка, вариант задания, справочная литература
2. Контрольно-оценочные материалы (КОМ)
Инструкция для обучающихся по выполнению контрольной работы
На выполнение письменной экзаменационной работы по математике дается 2 астрономических часа (90 минут).
Экзаменационная работа состоит из 2-х частей: обязательной и дополнительной.
Обязательная часть содержат задания минимально обязательного уровня, а дополнительная часть – более сложные задания.
При выполнении большинства заданий обязательной части требуется представить ход решения и указать полученный ответ. Только в нескольких заданиях достаточно представить ответ. За правильное выполнение любого задания из обязательной части вы получаете один балл. Если вы приводите неверное решение, неверный ответ или не приводите никакого ответа, получаете 0 баллов за задание.
При выполнении любого задания дополнительной части необходимо подробно описать ход решения и дать ответ.
Правильное выполнение заданий дополнительной части оценивается 3 баллами.
Баллы, полученные за все выполненные задания, суммируются.
Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов.
Перед началом работы внимательно ознакомьтесь со шкалой перевода баллов в отметки и обратите внимание, что начинать работу следует с заданий обязательной части.
Шкала перевода баллов в отметки по пятибалльной системе
| Отметка | Число баллов, необходимое для получения отметки |
| «3» (удовлетворительно) | 9 баллов – 13 баллов |
| «4» (хорошо) | 14 баллов – 19 баллов (не менее двух заданий из № 10-14 и одного задания из дополнительной части) |
| «5» (отлично) | 20 баллов и более (не менее двух заданий из дополнительной части) |
Желаем успехов!
1 вариант
Обязательная часть
При выполнении заданий 1-3 запишите ход решения и полученный ответ.
1. (1 балл) Найдите корень уравнения 32 - 2х = 81.
2. (1 балл) Решить уравнение sin (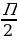 – х) = sin
– х) = sin 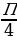
3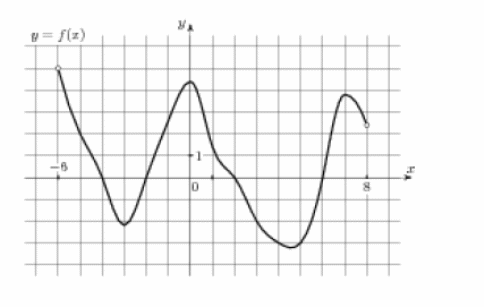 . (1 балл) На рисунке (см. ниже) изображен график функции
. (1 балл) На рисунке (см. ниже) изображен график функции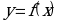 . Укажите область определения функции
. Укажите область определения функции
4. (1 балл) Определите наименьшее и наибольшее значения функции.
5. (1 балл) При каких значениях х, f(х) ≥ 0.
6. (1 балл) При каких значениях х, f(x) ≤ 0.
7. (1 балл) Найдите значение sinα, если известно, что cosα = 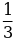 и α
и α 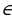 I четверти.
I четверти.
8. (1 балл) Решите уравнение log5(5 – 5x) = 2log52.
9 . (1 балл) Точки М и N расположены на ребрах треугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
. (1 балл) Точки М и N расположены на ребрах треугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
Шкала перевода баллов в отметки по пятибалльной системе
| Отметка | Число баллов, необходимое для получения отметки |
| «3» (удовлетворительно) | 9 баллов – 13 баллов |
| «4» (хорошо) | 14 баллов – 19 баллов (не менее двух заданий из № 10-14 и одного задания из дополнительной части) |
| «5» (отлично) | 20 баллов и более (не менее двух заданий из дополнительной части) |
Желаем успехов!
2 вариант
Обязательная часть
При выполнении заданий 1-9 запишите ход решения и полученный ответ.
1. (1 балл) Найдите корень уравнения 2 1 - х = 16.
2. (1 балл) Решите уравнение cos (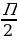 - х) = cos
- х) = cos 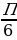
3 . (1 балл) На рисунке (см. ниже) изображен график функции
. (1 балл) На рисунке (см. ниже) изображен график функции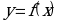 . Укажите область определения функции
. Укажите область определения функции
4. (1 балл) Определите наименьшее и наибольшее значения функции.
5. (1 балл) При каких значениях х, f(х) ≥ 0.
6. (1 балл) При каких значениях х, f(x) ≤ 0.
7. (1 балл) Найдите значение cos α, если известно, что sin α = 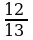 и α
и α 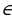 I четверти.
I четверти.
8. (1 балл) Решите уравнение log3 ( 2 - 2x ) = 2log3 4.
9 . (1 балл) Точки М и N расположены на ребрах четырехугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
. (1 балл) Точки М и N расположены на ребрах четырехугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
При выполнении заданий 10-14 запишите ход решения и полученный ответ.
10. (1 балл) В равнобедренном треугольнике ABC с основанием AC боковая сторона
AB равна 8, а cos A = 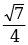 . Найдите высоту, проведенную к основанию.
. Найдите высоту, проведенную к основанию.
11. (1балл) Найдите объем тела, полученного при вращении прямоугольного треугольника с катетом 6 см и гипотенузой 10 см вокруг большего катета.
12. (1 балл) В правильной четырехугольной пирамиде высота равна 12 см, а высота боковой
грани 15 см. Найдите боковое ребро.
13. (1 балл) Решить уравнение 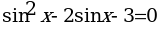 .
.
14. (1 балл) Решите неравенство log3 (5x – 6) log3 3
Дополнительная часть
При выполнении заданий 15 - 18 запишите ход решения и полученный ответ.
15. (3 балла) Укажите промежутки возрастания и убывания функции у = - 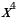 + 4
+ 4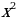 - 3
- 3
16. (3 балла) Решите систему уравнений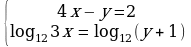 .
.
17. (3 балла) Равнобочная трапеция с основаниями 10 см и 18 см и высотой 3 см
вращается около меньшего основания. Найдите площадь поверхности тела
вращения.
18. (3 балла) Дана функция f(x) = 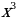 - 3
- 3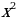 + 5. Найдите координаты точек ее графика, в которых касательные к нему параллельны оси абсцисс.
+ 5. Найдите координаты точек ее графика, в которых касательные к нему параллельны оси абсцисс.
При выполнении заданий 10 - 14 запишите ход решения и полученный ответ.
10. (1 балл) В треугольнике ABC AC = BC, AB = 6, cos A = 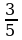 . Найдите высоту CH.
. Найдите высоту CH.
11. (1балл) Найдите площадь боковой поверхности тела, полученного при вращении прямоугольного треугольника с катетом 3 см и противолежащим углом 30° вокруг большего катета.
12. В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое ребро 13 см. Найдите высоту пирамиды.
13. (1 балл) Решить уравнение 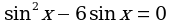 .
.
14. (1 балл) Решите неравенство 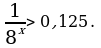
Дополнительная часть
При выполнении заданий 15 - 18 запишите ход решения и полученный ответ.
15. (3 балла) Найдите наименьшее и наибольшее значения функции у = 3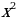 – 12х + 1 на
– 12х + 1 на
промежутке 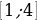
16. (3 балла) Решите систему уравнений 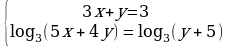 .
.
17. (3 балла) Равнобочная трапеция с основаниями 12 см и 18 см и высотой 4 см
вращается около большего основания. Найдите объём тела вращения.
18. (3 балла) Найдите угловой коэффициент касательной, проведенной к графику функции
f(x) = 6 sin x – cos x в его точке с абсциссой х = 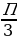






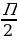 – х) = sin
– х) = sin 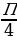
 . (1 балл) На рисунке (см. ниже) изображен график функции
. (1 балл) На рисунке (см. ниже) изображен график функции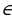 I четверти.
I четверти. . (1 балл) Точки М и N расположены на ребрах треугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
. (1 балл) Точки М и N расположены на ребрах треугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды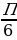
 . (1 балл) На рисунке (см. ниже) изображен график функции
. (1 балл) На рисунке (см. ниже) изображен график функции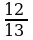 и α
и α  . (1 балл) Точки М и N расположены на ребрах четырехугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды
. (1 балл) Точки М и N расположены на ребрах четырехугольной пирамиды. Отметьте и обозначьте точки, в которых прямая МN пересекает прямые, содержащие другие ребра пирамиды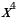 + 4
+ 4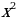 - 3
- 3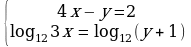 .
.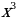 - 3
- 3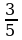 . Найдите высоту CH.
. Найдите высоту CH. 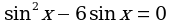 .
.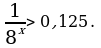
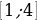
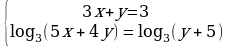 .
.