Вариант I
1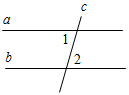 . Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
. Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
Найти: все образовавшиеся углы.
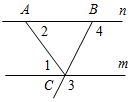
2. Дано:∠l = ∠2, ∠3 = 130°.
Найти:∠4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ∠ВАС = 72°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BDE = ∠BAC, то ∠BED = ∠BCA.
Вариант I
1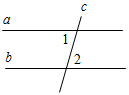 . Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
. Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
Найти: все образовавшиеся углы.

2. Дано:∠l = ∠2, ∠3 = 130°.
Найти:∠4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ∠ВАС = 72°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BDE = ∠BAC, то ∠BED = ∠BCA.
В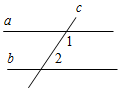 ариант II
ариант II
1. Дано: а || b, с – секущая, ∠1 – ∠2 = 106°.
Найти: все образовавшиеся углы.
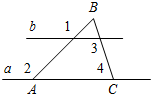
2. Дано:∠1 = ∠2, ∠3 = 120°.
Найти:∠4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ∠САЕ = 78°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BED = ∠BCA, то ∠BDE = ∠BAC.
В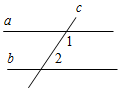 ариант II
ариант II
1. Дано: а || b, с – секущая, ∠1 – ∠2 = 106°.
Найти: все образовавшиеся углы.

2. Дано:∠1 = ∠2, ∠3 = 120°.
Найти:∠4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ∠САЕ = 78°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BED = ∠BCA, то ∠BDE = ∠BAC.
Вариант I
1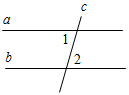 . Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
. Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
Найти: все образовавшиеся углы.

2. Дано:∠l = ∠2, ∠3 = 130°.
Найти:∠4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ∠ВАС = 72°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BDE = ∠BAC, то ∠BED = ∠BCA.
В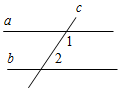 ариант II
ариант II
1. Дано: а || b, с – секущая, ∠1 – ∠2 = 106°.
Найти: все образовавшиеся углы.

2. Дано:∠1 = ∠2, ∠3 = 120°.
Найти:∠4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если ∠САЕ = 78°.
4. На сторонах АВ и ВС треугольника АВС отмечены точки D и Е соответственно. Докажите, что если ∠BED = ∠BCA, то ∠BDE = ∠BAC.





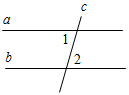 . Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
. Дано: а || b, с – секущая, ∠1 + ∠2 = 104°.
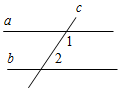 ариант II
ариант II










