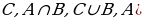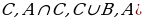Контрольная работа по теме"Множества. Вероятность событий. Независимые и несовместные события. Дисперсия"

Контрольная работа №2

Вариант 1

№1. На зачете по химии 78 вопросов, 9 из них по теме «Металлы». Лина не выучила тему «Металлы». Найдите вероятность того, что ей попадется выученный билет.

№2. На олимпиаде по литературе школьнику достается один вопрос из списка. Вероятность того, что этот вопрос по теме "Достоевский", равна 0,33. Вероятность того, что это окажется вопрос по теме «Толстой» равна 0,24. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на олимпиаде школьнику достанется вопрос по одной из этих двух тем.

№3. Правильный игральный кубик бросают два раза. Постройте таблицу элементарных событий при бросании двух игральных кубиков. Найдите вероятность того, что сумма выпавших очков окажется не меньше 7.

№4. Би­ат­ло­нист четыре раза стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,7. Най­ди­те ве­ро­ят­ность того, что би­ат­ло­нист пер­вые три раза попал в ми­ше­ни, а один про­мах­нул­ся. Ре­зуль­тат округ­ли­те до сотых.

№5. Запишите множества (используя рис. Большие буквы А,В,С – обозначение множеств):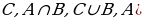

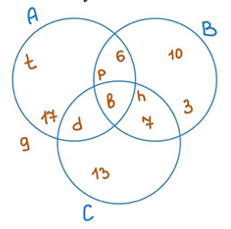
№6. Для чисел –2, –6, 2, 6, 5 вычислите среднее значение, отклонения и дисперсию.

Контрольная работа №2

Вариант 2

№1. Производство собирает принтеры. В среднем 12 из 272 имеют проблемы с лотком приема бумаги. Найдите вероятность того, что наудачу купленный принтер не будет иметь проблем с лотком приема бумаги.

№2. Вероятность того, что на зачете вам попадется билет, который содержит вопрос по теме «Треугольники» равна 0,4. Вероятность того, что вам попадется билет, который содержит вопрос по теме «Четырехугольник» равна 0,23. В списке нет вопросов, которые одновременно относятся к этим двум темам. Найдите вероятность того, что вам попадется билет, содержащий вопрос хотя бы по одной из этих тем.

№3. Правильный игральный кубик бросают два раза. Постройте таблицу элементарных событий при бросании двух игральных кубиков. Найдите вероятность того, что сумма выпавших очков окажется не больше 6.

№4. Би­ат­ло­нист пять раз стре­ля­ет по ми­ше­ням. Ве­ро­ят­ность по­па­да­ния в ми­шень при одном вы­стре­ле равна 0,8. Най­ди­те ве­ро­ят­ность того, что би­ат­ло­нист пер­вые два раза попал в ми­ше­ни, а три раза про­мах­нул­ся. Ре­зуль­тат округ­ли­те до сотых.

№5. Запишите множества (используя рис. Большие буквы А,В,С – обозначение множеств):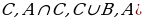

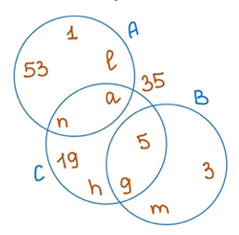
№6. Для чисел –2, –1, 1, 2, 5 вычислите среднее значение, отклонения и дисперсию.