Зимняя сессия 11 класс. Профиль Вариант1.
1. Железнодорожный билет для взрослого стоит 840 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 18 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?
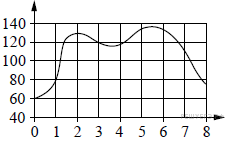
2. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в период с января по апрель 1994 года. Ответ дайте в градусах Цельсия.

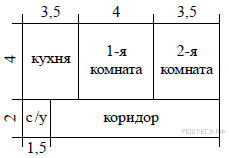
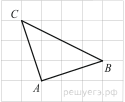
3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

4. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 69 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 69 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент А. получит не менее 69 баллов по математике, равна 0,6, по русскому языку — 0,6, по иностранному языку — 0,6 и по обществознанию — 0,9.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.
5. Решите уравнение 
6. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
7. Материальная точка движется прямолинейно по закону 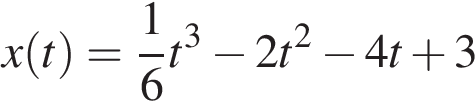 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 38 м/с?
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 38 м/с?
8. Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на 

9. Найдите значение выражения 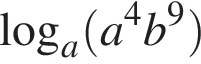 , если
, если 
10. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление 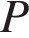 (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле
(в паскалях), оказываемое навесом и колонной на опору, определяется по формуле  , где
, где 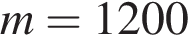 кг – общая масса навеса и колонны,
кг – общая масса навеса и колонны,  – диаметр колонны (в метрах). Считая ускорение свободного падения
– диаметр колонны (в метрах). Считая ускорение свободного падения  м/с
м/с , а
, а  , определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400 000 Па. Ответ выразите в метрах.
11. На изготовление 780 деталей первый рабочий тратит на 4 часа меньше, чем второй рабочий на изготовление 840 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей за час делает первый рабочий?
12. Найдите точку минимума функции 
13. а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14. Основанием прямой четырехугольной призмы ABCDA'B'C'D' является квадрат ABCD со стороной  , высота призмы равна
, высота призмы равна  Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
15. Решите неравенство 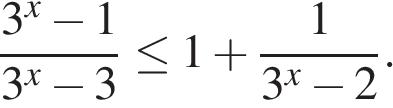
16. В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
17. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
18. При каждом а решите систему уравнений
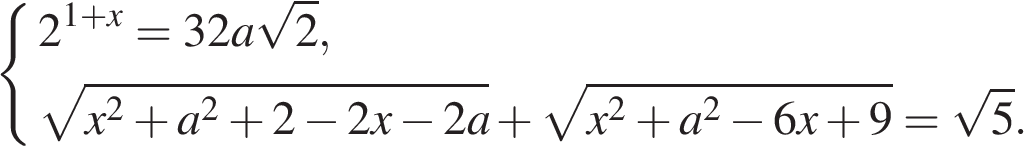
19. Каждый из группы учащихся сходил в кино или в театр, при этом возможно, что кто-то из них мог сходить и в кино, и в театр. Известно, что в театре мальчиков было не более  от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более
от общего числа учащихся группы, посетивших театр, а в кино мальчиков было не более  от общего числа учащихся группы, посетивших кино.
от общего числа учащихся группы, посетивших кино.
а) Могло ли быть в группе 10 мальчиков, если дополнительно известно, что всего в группе было 20 учащихся?
б) Какое наибольшее количество мальчиков могло быть в группе, если дополнительно известно, что всего в группе было 20 учащихся?
в) Какую наименьшую долю могли составлять девочки от общего числа учащихся в группе без дополнительного условия пунктов а) и б)?












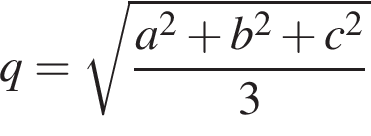 . Найдите среднее квадратичное чисел
. Найдите среднее квадратичное чисел 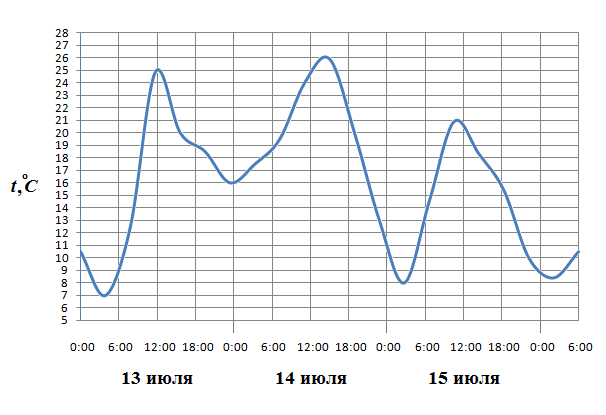





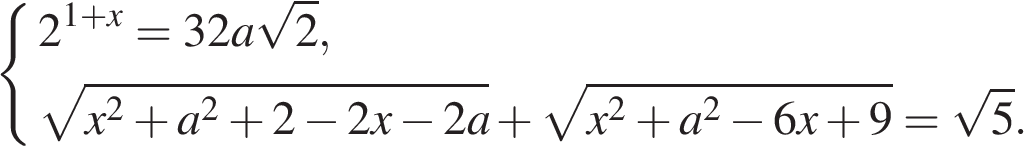





 имеет ровно два решения.
имеет ровно два решения.









