Россия, Луговое
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 05.03.2025 13:53
Катаева Анна Владиславовна
учитель математики
44 года
17 806
1 865 
Местоположение
Специализация
Контрольная работа за год по алгебре 7 класс. Мерзляк
Категория:
Алгебра
21.03.2022 10:55
Просмотр содержимого документа
«Контрольная работа за год по алгебре 7 класс. Мерзляк»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к аттестационному материалу
для проведения промежуточной аттестации
для учащихся 7 класса по алгебре
2021-2022 учебный год
Назначение аттестационной работы-оценка уровня подготовки обучающихся по данному предмету, определение перспектив индивидуальной работы с обучающимися в следующем году.
Промежуточная аттестация по алгебре в 7 классе проводится в соответствии с:
1. Приказа Министерства образования и науки Российской Федерации «Об утверждении федерального государственного образовательного стандарта основного общего образования от 17.12.2010 г. № 1897 (в редакции Приказов Минобрнауки России от 29.12.2014 г. № 1644, от 31.12.2015 г. №1577)
2. Приказов Министерства просвещения Российской Федерации:
- «Об утверждении федерального перечня учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования организациями, осуществляющими образовательную деятельность» от 20.05.2020 №254 (с изменениями от 23.12.2020 г., приказ №766);
- О внесении изменений в некоторые федеральные государственные образовательные стандарты общего образования по вопросам воспитания обучающихся» от 11.12.2020 №712.
3. Примерной основной образовательной программы основного общего образования
(одобренной Федеральным учебно-методическим объединением по общему образованию. Протокол заседания от 8 апреля 2015 г. № 1/15, ред. от 04.02.2020)
4. Основная образовательная программа основного общего образования МАОУ Луговской СОШ, в ред. от 28.11.2018 г., приказ № 69 -ОД, изменения внесены педагогическим советом, протокол № 4 от 26.11.2018 г.
5.Учебного плана МАОУ Луговской СОШ на 2021-2022 учебный год, утвержденного приказом директора школы №150/ОД от 16.08.2021г., принятым на педагогическом совете – протокол №10 от 16.08.2021г. и согласованным с Управляющим советом – протокол №12 от 16.08.2021г.
6. Рабочей программы воспитания МАОУ Луговской СОШ, утвержденной приказом директора школы №150/ОД от 16.08.2021г., принятой на педагогическом совете – протокол №10 от 16.08.2021г. и согласованной с Управляющим советом – протокол №12 от 16.08.2021г.
7.Положение о формах, периодичности и порядке текущего контроля успеваемости, промежуточной и итоговой аттестации обучающихся МАОУ Луговской СОШ, утвержденное приказом от 28.11.2018 г. № 61-ОД.
8. В соответствии с авторской программой А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко (Математика: программы 5–9 классы А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко /. — М. : Вентана-Граф, 2013. — 112 с.)
Содержание и структура работы для промежуточной аттестации по алгебре разработана на основе:
- Федерального компонента государственного стандартного образования, утвержденного приказом Минобразования России от 5 марта 2004 года № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного и среднего (полного) общего образования»;
- Приказом Министерства образования РФ от 31.03.2014 г. № 253 (ред. От 05.07.2017) «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего и среднего(полного) общего образования».
Содержание работы. Итоговая контрольная работа состоит из 6 заданий. Всего 4 варианта работы.
| № задания | Задание |
| Количество баллов |
| 1 | Упростите выражение | -Формулы сокращенного умножения: квадрат суммы или разности двух выражений; -умножение многочлена на многочлен; -приведение многочлена в стандартный вид;
| 3б-Задание выполнено верно (приведено полное обоснованное решение) 2б-Задание решено верно, но отсутствует обоснование решения ИЛИ ход решения верный, все шаги присутствуют, но получен неверный ответ из-за ошибки/описки вычислительного характера 1б- Выбран верный ход рассуждений, но решение не доведено до конца (выполнено верно не менее 2/3 задания) |
| 2 | Разложите на множители | -формулы сокращенного умножения; - вынесение общего множителя за скобки | 3- Выполнены верно два пункта задания(приведено полное обоснованное решение) 2- Выполнен верно один пункт задания и допущена ошибка во втором пункте задания вычислительного характера, с её учётом дальнейшие шаги выполнены верно 1- Выполнен верно один пункт задания |
| 3 | Найти значение коэффициентов в формуле графика линейной функции | -Нахождение неизвестного коэффициентов; -линейная функция;
| 3- Задание выполнено верно (приведено полное обоснованное решение) 2-Задание решено верно, но отсутствует обоснование решения ИЛИ ход решения верный, все шаги присутствуют, значение k ( b) найдено верно, а при нахождении b (k ) получен неверный ответ из-за ошибки/описки вычислительного характера 1- Выбран верный ход рассуждений, но решение не доведено до конца (выполнено верно не менее 2/3 задания) |
| 4 | Решить систему уравнений | -решение системы линейных уравнений; -нахождение неизвестного компонента;
| 2-выполнены все преобразования для нахождения неизвестного, все действия выполнены без ошибок 1- выполнены все преобразования для нахождения неизвестного, в вычислениях допущена одна ошибка |
| 5 | Решение задачи | -составление
| 3- Приведено верное обоснованное решение задачи, получен верный ответ 2- Задача решена верно, но отсутствует обоснование решения ИЛИ ход решения верный, все шаги присутствуют, но получен неверный ответ из-за ошибки/описки вычислительного характера 1- Выбран верный ход рассуждений, но решение не доведено до конца (выполнено верно не менее 2/3 задания) |
| 6 | Решить уравнение | -Нахождение неизвестного компонента -решение уравнения с двумя переменными
| 3- Задание выполнено верно (приведено полное обоснованное решение) 2-Задача решена верно, но отсутствует обоснование решения ИЛИ ход решения верный, все шаги присутствуют, но получен неверный ответ из-за ошибки/описки вычислительного характера 1- Выбран верный ход рассуждений, но решение не доведено до конца (выполнено верно не менее 2/3 задания) |
Максимальный балл всей контрольной работы 17 баллов
Перевод первичного балла в отметку:
16-17 баллов – «5» (95% - 100 %)
12-15 баллов – «4» (70 % - 94%)
8-11 баллов – «3» (50 % - 69%)
0–7 баллов – «2» (менее 50 %)
Содержание и структура промежуточного контроля по алгебре в 7 классе дают возможность достаточно полно проверить комплекс умений и навыков:
Упрощение выражений, используя формулы сокращенного умножения;
Умножение многочлена на многочлен;
Приведение многочлена в стандартный вид;
Вынесение общего множителя за скобки;
Решение системы уравнений;
Решение уравнения с двумя переменными;
Нахождение коэффициентов в формуле линейной функции, проходящей через заданные точки.
Ответы на итоговую аттестацию по алгебре в 7 классе:
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1 | 9а2-51а+23 | 6а2-22а-1 | 8а2+26а+12 | b2+24b+40 |
| 2 | 1)5у2(х-9с)(х+9с) 2) 2(x+6y)2 | 1)3m2(n-4p)(n+4p) 2)3(x+2y)2 | 1)7c2(a-2b)(a+2b) 2)5(a-3b)2 | 1)6a2(b-10c)(b+10c) 2)7(a-2b)2 |
| 3 | k=2 и b=-6 | k=3 и b=15 | k=-4 и b=-12 | k=9 и b=-36 |
| 4 | (4;-5) | (3;2) | (1;-3) | (-4;-9) |
| 5 | 4,5,6,7 | 7,8,9,10 | 9,10,11,12 | 14,15,16,17 |
| 6 | х=1,у=-3 | х=-2,у=4 | х=4,у=-1 | х=6,у=-2 |
При составлении аттестационного материала использована следующая литература:
Авторской программы Мерзляк А.Г. Математика: программы: 5-9 классы / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В. Буцко. -2 изд.,дораб.-М.: Вентана-Граф,2017.
Алгебра. 7 класс: учебник для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. - М.: Вентана-Граф, 2020
Вариант 1
Упростите выражение (5a − 4)2 − (2a − 1)(3a + 7).
Разложите на множители: 1) 5x2y2 − 45y2c2; 2) 2x2 + 24xy + 72y2.
График функции y = kx + b пересекает оси координат в точках A(0; −6) и B(3; 0). Найдите значения k и b.
Решите систему уравнений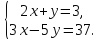 
Найдите четыре последовательных натуральных числа таких, что
произведение третьего и четвёртого из этих чисел на 22 больше произведения первого и второго.
Решите уравнение x2 + y2 − 2x + 6y + 10 = 0.
Вариант 2
Упростите выражение (3a − 2)2 − (3a + 1)(a + 5).
Разложите на множители: 1) 3m2n2 − 48m2p2; 2) 3x2 + 12xy + 12y2.
График функции y = kx + b пересекает оси координат в точках C (0; 15) и D (−5; 0). Найдите значения k и b.
Решите систему уравнений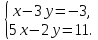 
Найдите четыре последовательных натуральных числа таких, что
произведение первого и третьего из этих чисел на 17 меньше произведения второго и четвёртого.
Решите уравнение x2 + y2 + 4x − 8y + 20 = 0.
Вариант 3
Упростите выражение (4a + 3)2 − (2a + 1)(4a − 3).
Разложите на множители: 1) 7a2c2 − 28b2c2; 2) 5a2 − 30ab + 45b2.
График функции y = kx + b пересекает оси координат в точках M (0; −12) и K (−3; 0). Найдите значения k и b.
Решите систему уравнений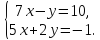 
Найдите четыре последовательных натуральных числа таких, что
произведение четвёртого и третьего из этих чисел на 42 больше произведения первого и второго.
Решите уравнение x2 + y2 − 8x + 2y + 17 = 0.
Вариант 4
Упростите выражение (2b + 5)2 − (b − 3)(3b + 5).
Разложите на множители: 1) 6a2b2 − 600a2c2; 2) 7a2 − 28ab + 28b2.
График функции y = kx + b пересекает оси координат в точках E (0; −36) и F (4; 0). Найдите значения k и b.
Решите систему уравнений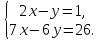 
Найдите четыре последовательных натуральных числа таких, что
произведение первого и третьего из этих чисел на 31 меньше произведения второго и четвёртого.
Решите уравнение x2 + y2 − 12x + 4y + 40 = 0.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
