Россия, С.Красная Криуша
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 12.12.2024 22:42
Кречетова Ирина Николаевна
Учитель математики
60 лет
873
66 490 
Местоположение
Специализация
Контрольно-измерительные материалы по алгебре 11 класс
Категория:
Математика
04.12.2024 21:44
Просмотр содержимого документа
«Контрольно-измерительные материалы по алгебре 11 класс»
Приложение
к рабочей программе по информатике
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА
по математике (модуль «Алгебра»)
10 класс
Контрольно-оценочные средства
Структура и содержание
Паспорт КОС
| Раздел, тема | Проверяемые компетенции (из рабочей программы) | Вид оценочных средств (контрольная работа, тест, диктант, тестирование в формате ОГЭ, ЕГЭ и т.д.) | Вариативность |
| Повторение и расширение сведений о функции | Формулировать определения наибольшего и наименьшего значений функции, чётной и нечётной функций. Формулировать теоремы о свойствах графиков чётных и нечётных функций. Находить наибольшее и наименьшее значения функции на множестве по её графику. Исследовать функцию, заданную формулой, на чётность. Строить графики функций, используя чётность или нечётность. Выполнять геометрические преобразования графиков функций, связанные с параллельными переносами, растяжениями, сжатиями и симметриями, относительно координатных осей. Формулировать определение обратимой функции. Распознавать обратимую функцию по её графику. Устанавливать обратимость функции по её возрастанию или убыванию. Формулировать определение взаимно обратных функций. Проверять, являются ли две данные функции взаимно обратными. Находить обратную функцию к данной обратимой функции. По графику данной функции строить график обратной функции. Устанавливать возрастание (убывание) обратной функции по возрастанию (убыванию) данной функции. Формулировать определения области определения уравнений (неравенств), равносильных уравнений (неравенств), уравнений-следствий (неравенств-следствий), постороннего корня. Формулировать теоремы, описывающие равносильные преобразования уравнений (неравенств). Применять метод равносильных преобразований для решения уравнений и неравенств. Находить область определения уравнений и неравенств. Применять метод следствий для решения уравнений. Решать неравенства методом интервалов | Входная контрольная работа. Контрольная работа. № 1 | 2
2
|
| Степенная функция | Формулировать определение степенной функции с целым показателем. Описывать свойства степенной функции с целым показателем, выделяя случаи чётной и нечётной степени, а также натуральной, нулевой и целой отрицательной степени. Строить графики функций на основе графика степенной функции с целым показателем. Находить наибольшее и наименьшее значения степенной функции с целым показателем на промежутке. Формулировать определение корня (арифметического корня) n-й степени, а также теоремы о его свойствах, выделяя случаи корней чётной и нечётной степени. Находить области определения выражений, содержащих корни n-й степени. Решать уравнения, сводящиеся к уравнению xn=a. Выполнять тождественные преобразования выражений, содержащих корни n-й степени, в частности, выносить множитель из-под знака корня n-й степени, вносить множитель под знак корня n-й степени, освобождаться от иррациональности в знаменателе дроби. Описывать свойства функции y =, выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции y=. Формулировать определение степени с рациональным показателем, а также теоремы о её свойствах. Выполнять тождественные преобразования выражений, содержащих степени с рациональным показателем. Распознавать иррациональные уравнения и неравенства. Формулировать теоремы, обосновывающие равносильность уравнений (неравенств) при возведении обеих частей данного уравнения (неравенства) в натуральную степень. Решать иррациональные уравнения методом равносильных преобразований и методом следствий. Решать иррациональные неравенства методом равносильных преобразований | Контрольная работа № 2 Контрольная работа № 3
| 2
2
|
| Тригонометрическая функция | Формулировать определение радианной меры угла. Находить радианную меру угла по его градусной мере и градусную меру угла по его радианной мере. Вычислять длины дуг окружностей. Формулировать определения косинуса, синуса, тангенса и котангенса угла поворота. Выяснять знак значений тригонометрических функций. Упрощать тригонометрические выражения, используя свойства чётности тригонометрических функций. Формулировать определения периодической функции, её главного периода. Упрощать тригонометрические выражения, используя свойства периодичности тригонометрических функций. Описывать свойства тригонометрических функций. Строить графики функций на основе графиков четырёх основных тригонометрических функций. Преобразовывать тригонометрические выражения на основе соотношений между тригонометрическими функциями одного и того же аргумента. По значениям одной тригонометрической функции находить значения остальных тригонометрических функций того же аргумента. Преобразовывать тригонометрические выражения на основе формул сложения. Опираясь на формулы сложения, доказывать формулы приведения, формулы двойных углов, формулы суммы и разности синусов (косинусов), формулы преобразования произведения тригонометрических функций в сумму. Преобразовывать тригонометрические выражения на основе формул приведения, формул двойных и половинных углов, формул суммы и разности синусов (косинусов), формул преобразования произведения тригонометрических функций в сумму | Контрольная работа № 4 Контрольная работа № 5
| 2
2
|
| Тригонометрические уравнения и неравенства | Формулировать определения арккосинуса, арксинуса, арктангенса, арккотангенса. Находить значения обратных тригонометрических функций в отдельных табличных точках. Используя понятия арккосинуса, арксинуса, арктангенса, арккотангенса, решать простейшие тригонометрические уравнения. Формулировать свойства обратных тригонометрических функций. Строить графики функций на основе графиков четырёх основных обратных тригонометрических функций. Упрощать выражения, содержащие обратные тригонометрические функции. Распознавать тригонометрические уравнения и неравенства. Решать тригонометрические уравнения, сводящиеся к алгебраическим уравнениям, в частности, решать однородные тригонометрические уравнения первой и второй степени, а также решать тригонометрические уравнения, применяя метод разложения на множители. Решать простейшие тригонометрические неравенства | Контрольная работа № 6
| 2 |
| Производная и её применение | познакомиться с понятием предела, составлять уравнение касательной и уметь исследовать функцию на монотонность и экстремумы. | Контрольная работа № 7 Контрольная работа № 8
| 2
2 |
| Повторение |
| Итоговая контрольная работа | 2 |
2. КИМ с критериями оценки
Оценка письменных контрольных работ обучающихся по математике
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
При выполнении контрольной работы:
Содержание и объем материала, подлежащего проверке в контрольной работе, определяется программой. При проверке усвоения материала выявляется полнота, прочность усвоения учащимися теории и умение применять ее на практике в знакомых и незнакомых ситуациях.
Входная КР
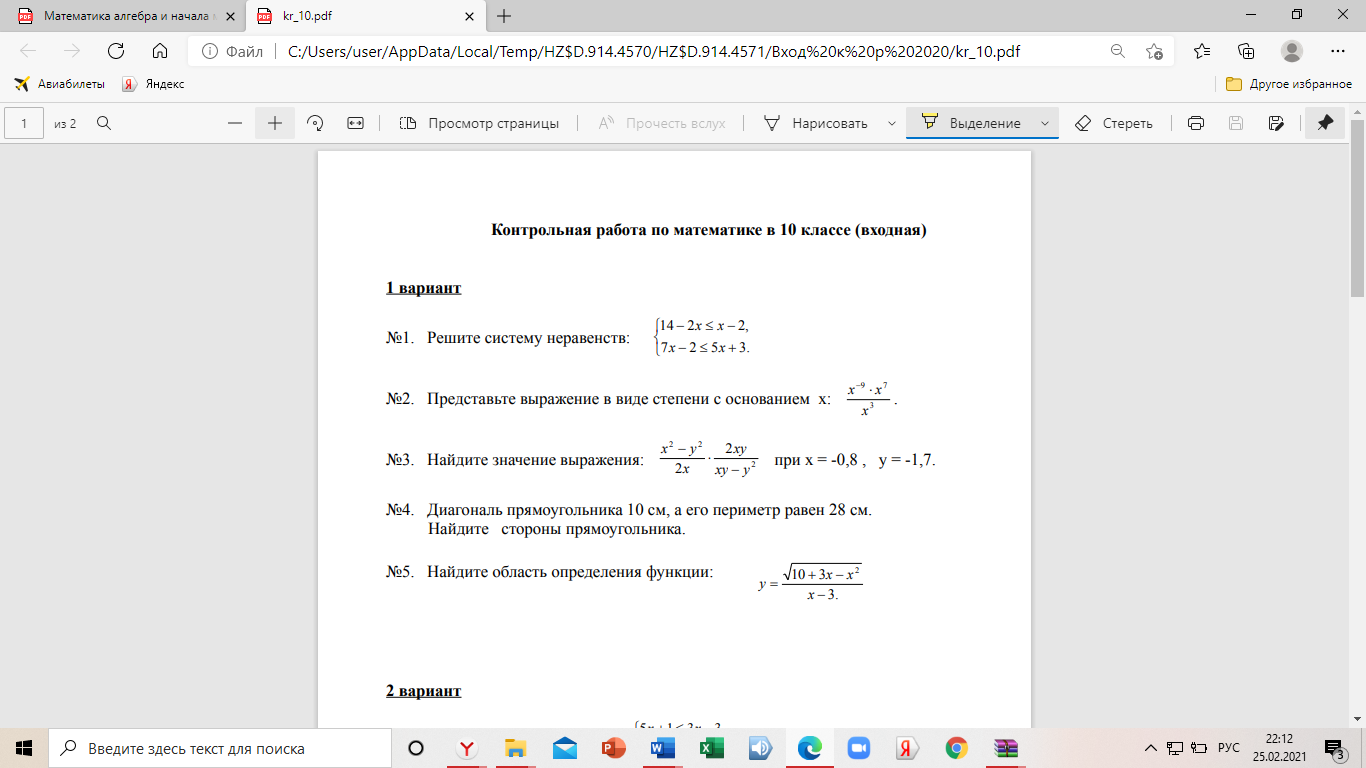
КР № 1 по теме «Повторение и расширение сведений о функции»
Вариант 1
1. Найдите наибольшее и наименьшее значения функции:
1) на промежутке [2; 1];
2) на промежутке [0; 3].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
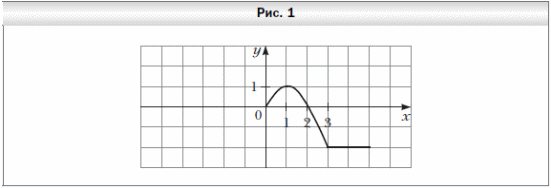
6. На рисунке 1 изображена часть графика чётной функции y = f(x), определённой на промежутке [5; 5]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [5; 5].
7. Решите неравенство:
1)
2)
3)
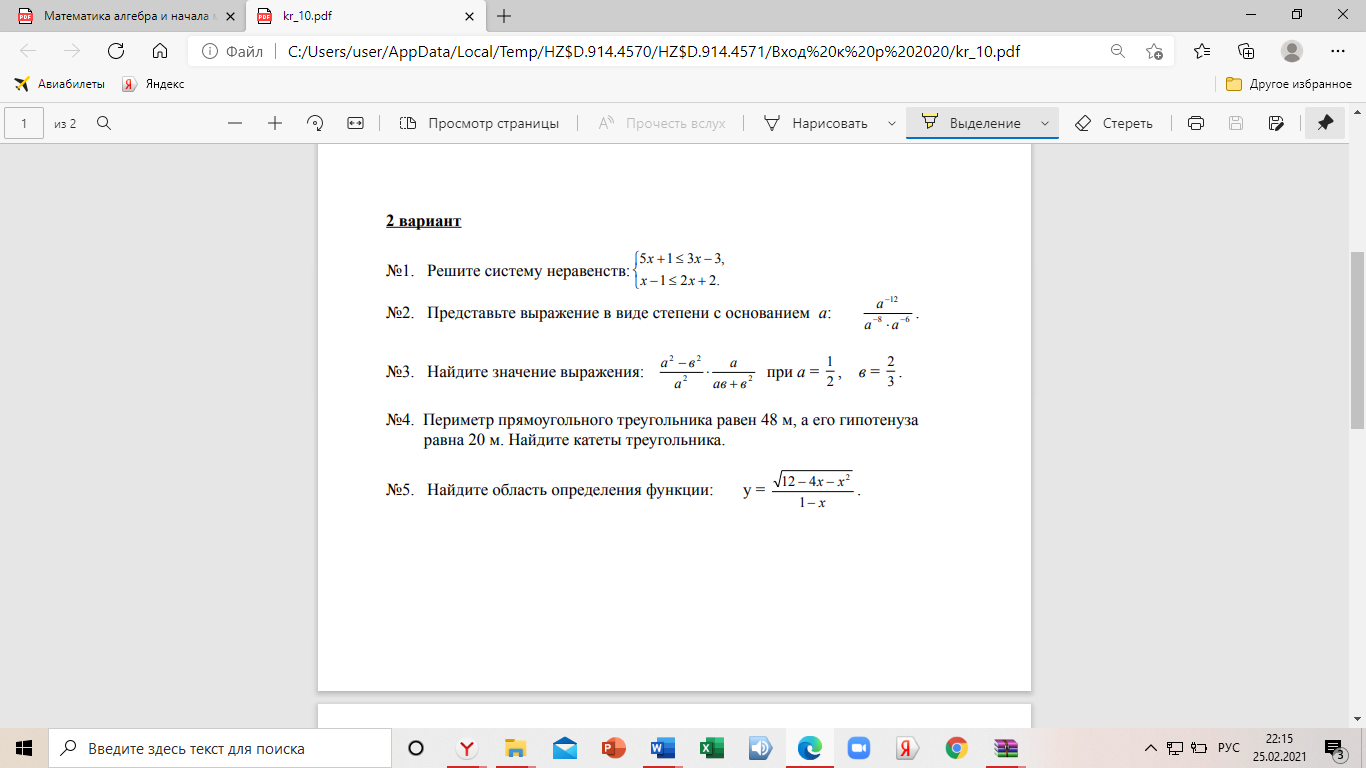
КР № 1 Вариант 2
1. Найдите наибольшее и наименьшее значения функции:
1) на промежутке [3; 2];
2) на промежутке [-3; 0].
2. Исследуйте на чётность функцию:
1)
2)
3. Найдите функцию, обратную к функции
4. Постройте график функции
5. Являются ли равносильными уравнения:
1)
2)
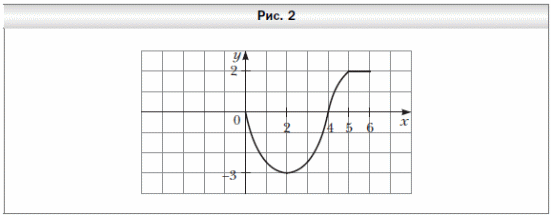
6. На рисунке 2 изображена часть графика нечётной функции y = f(x), определённой на промежутке [6; 6]. Достройте график этой функции и найдите её наибольшее и наименьшее значения на промежутке [6; 6].
7. Решите неравенство:
1)
2)
3)
КР № 2 по теме «Степенная функция. Корень n-й степени и его свойства»
Вариант 1
1. Функция задана формулой . Сравните:
1) и ; 3) и ;
2) и ; 4) и
2. Найдите значение выражения:
1) ; 3)
3) ; 4) .
3. Решите уравнение:
1) x5 6; 3) x5 5) ;
2) x4 16; 4) x4 81; 6)
4. Найдите наибольшее и наименьшее значения функции на промежутке [2; 4].
5. Упростите выражение:
1) ; 3) , если ;
2) ; 4) , если .
6. Определите графически количество решений системы уравнений
7. Освободитесь от иррациональности в знаменателе дроби:
1) ; 2)
8. Упростите выражение
КР № 2 Вариант 2
1. Функция задана формулой . Сравните:
1) и ; 3) и ;
2) и ; 4) и
2. Найдите значение выражения:
1) ; 3)
3) ; 4) .
3. Решите уравнение:
1) x7 10; 3) x3 5) ;
2) x6 64; 4) x4 16; 6)
4. Найдите наибольшее и наименьшее значения функции на промежутке [3; 1].
5. Упростите выражение:
1) ; 3) , если ;
2) ; 4) , если .
6. Определите графически количество решений системы уравнений
7. Освободитесь от иррациональности в знаменателе дроби:
1) ; 2)
8. Упростите выражение
КР № 3 по теме «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства»
Вариант 1
1. Найдите значение выражения:
1) ; 2) ; 3) ; 4) .
2. Упростите выражение:
1) ; 3) ; 5)
2) ; 4) 6)
3. Решите уравнение .
4. Сократите дробь:
1) ; 2) ; 3) .
5. Решите уравнение:
1) ; 2) .
6. Решите неравенство .
КР № 3 Вариант 2
1. Найдите значение выражения:
1) ; 2) ; 3) ; 4) .
2. Упростите выражение:
1) ; 3) ; 5)
2) ; 4) 6)
3. Решите уравнение .
4. Сократите дробь:
1) ; 2) ; 3) .
5. Решите уравнение:
1) ; 2) .
6. Решите неравенство .
КР № 4 по теме «Тригонометрические функции и их свойства»
Вариант 1
1. Найдите значение выражения .
2. Определите знак значения выражения:
1) 2)
3. Исследуйте на чётность функцию:
1) 2)
4. Найдите значение выражения:
1) 2)
5. Сравните значения выражений:
1) и ; 2) и
6. Постройте график функции , укажите её промежутки возрастания и убывания.
7. Постройте график функции
КР № 4 Вариант 2
1. Найдите значение выражения .
2. Определите знак значения выражения:
1) 2)
3. Исследуйте на чётность функцию:
1) 2)
4. Найдите значение выражения:
1) 2)
5. Сравните значения выражений:
1) и ; 2) и
6. Постройте график функции , укажите её промежутки возрастания и убывания.
7. Постройте график функции
КР № 5 по теме «Соотношение между тригонометрическими функциями одного и того же аргумента. Формулы сложения и их следствия»
Вариант 1
1. Упростите выражение:
1) 4)
2) 5)
3) 6)
2. Дано: . Найдите
3. Докажите тождество:
1)
2)
3)
4. Найдите наибольшее и наименьшее значения выражения
КР № 5 Вариант 2
1. Упростите выражение:
1) 4)
2) 5)
3) 6)
2. Дано: . Найдите
3. Докажите тождество:
1)
2)
3)
4. Найдите наибольшее и наименьшее значения выражения
КР № 6 по теме «Тригонометрические уравнения и неравенства»
Вариант 1
1. Решите уравнение:
2. Решите неравенство:
3. Решите уравнение:
1)
2)
3)
4. Решите уравнение
КР № 6 Вариант 2
1. Решите уравнение:
2. Решите неравенство:
3. Решите уравнение:
1)
2)
3)
4. Решите уравнение
КР № 7 по теме «Производная. Уравнение касательной»
Вариант 1
1. Найдите производную функции:
1) 3)
2) 4)
2. Составьте уравнение касательной к графику функции в точке с абсциссой = 3.
3. Материальная точка движется по координатной прямой по закону (перемещение s измеряется в метрах, время t — в секундах). Найдите скорость её движения в момент времени t0 = 3 с.
4. Найдите производную данной функции и вычислите её значение в точке x0:
1) = 13; 2) .
5. Найдите абсциссу точки графика функции в которой проведённая к нему касательная образует с положительным направлением оси абсцисс угол 30°.
6. Найдите уравнение касательной к графику функции если эта касательная параллельна прямой .
КР № 7 Вариант 2
1. Найдите производную функции:
1) 3)
2) 4)
2. Составьте уравнение касательной к графику функции в точке с абсциссой = 4.
3. Материальная точка движется по координатной прямой по закону (перемещение s измеряется в метрах, время t — в секундах). Найдите скорость её движения в момент времени t0 = 2 с.
4. Найдите производную данной функции и вычислите её значение в точке x0:
1) = 4; 2) .
5. Найдите абсциссу точки графика функции в которой проведённая к нему касательная образует с положительным направлением оси абсцисс угол 60°.
6. Найдите уравнение касательной к графику функции если эта касательная параллельна прямой .
КР № 8 по теме «Применение производной»
Вариант 1
1. Найдите промежутки возрастания и убывания и точки экстремума функции:
1) 2)
2. Найдите наибольшее и наименьшее значения функции на промежутке [−1; 2].
3. Представьте число 60 в виде суммы двух положительных чисел так, чтобы сумма их квадратов была наименьшей.
4. Исследуйте функцию и постройте её график.
5. При каких значениях a функция возрастает на R?
КР № 8 Вариант 2
1. Найдите промежутки возрастания и убывания и точки экстремума функции:
1) 2)
2. Найдите наибольшее и наименьшее значения функции на промежутке [0; 3].
3. Представьте число 36 в виде суммы двух положительных чисел так, чтобы их произведение было наибольшим.
4. Исследуйте функцию и постройте её график.
5. При каких значениях a функция убывает на R?
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
