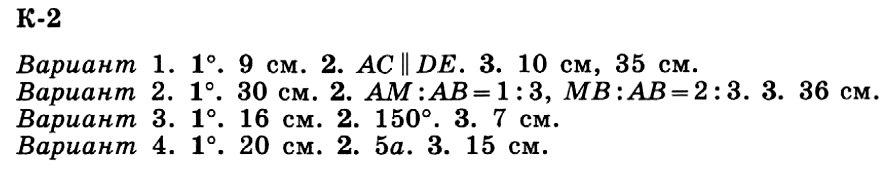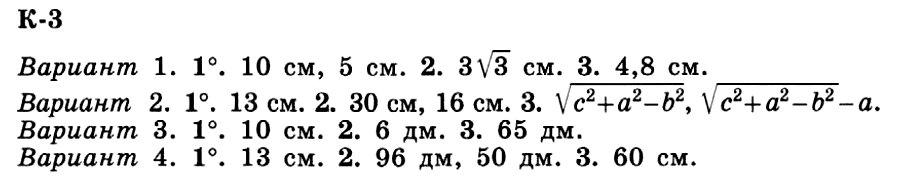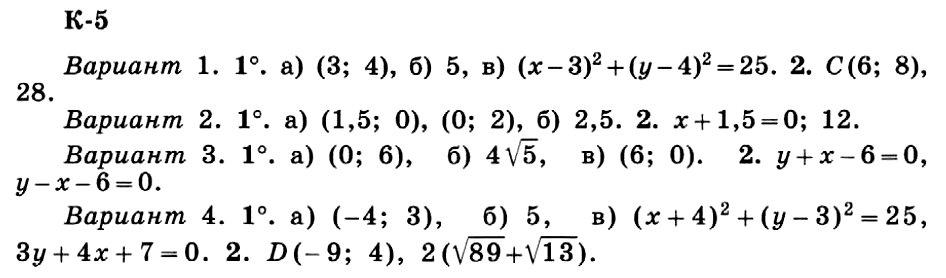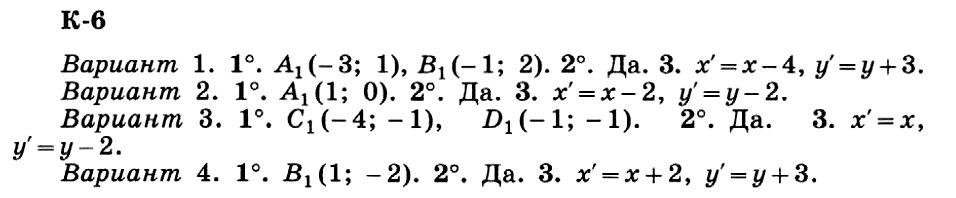Контрольно-измерительные материалы на 2019-2020 учебный год
Геометрия
8 класс
Входная контрольная работа
Цель: определение уровня учебной подготовки по предмету на начало учебного года.
Входная контрольная работа по геометрии
8 класс
Вариант 1
В задании №1выберите один верный ответ.
№1. Если один из смежных углов равен 34, то второй угол будет.
1)прямой
2)острый
3)развернутый
4)тупой
№2 Какое из следующих утверждений верно? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2)Если угол равен 108°, то вертикальный с ним равен 72°.
3 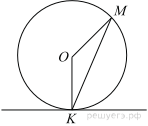 )Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
№3 Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 46°. Найдите величину угла OMK. Ответ дайте в градусах.
№4 В треугольнике ABC AC = BC. Внешний угол при вершине А равен 123°. Найдите угол C. Ответ дайте в градусах.
№5. В равнобедренном треугольнике один из углов равен 1200, боковая сторона 12 см. Найдите высоту, проведенную к основанию.
Входная контрольная работа по геометрии 8 класс Вариант 2
В задании №1выберите один верный ответ.
№1. Если один из смежных углов равен 98, то второй угол будет.
1)прямой
2)острый
3)развернутый
4)тупой
№2 Какое из следующих утверждений верно? Запишите их номера.
1) Если угол равен 54°, то вертикальный с ним равен 126°.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3  )Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180
)Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180 , то прямые параллельны.
, то прямые параллельны.
№3 Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 52°. Найдите величину угла OМК. Ответ дайте в градусах.
№4 В треугольнике ABC AВ = BC. Внешний угол при вершине С равен 137°. Найдите угол В. Ответ дайте в градусах.
№5. В равнобедренном треугольнике один из углов равен 1200, высота, проведенная к основанию 8 см. Найдите боковую сторону.
Ответы:
Вариант 1
№1 4
№2 13
№3 44°
№4 66°
№5 6 см
Вариант 2
№1 2
№2 23
№3 38°
№4 94°
№5 16 см
Система оценивания работы:
Задания №1-№2 оцениваются в 1 балл.
Задания №3-№5 второй части оцениваются в 2 балла.
| Задание | Кол-во баллов | Критерий оценивания |
| №3 | 0 баллов | Неверно найден угол. |
| | 1 балл | Ход решения верный, найден угол. Может быть допущена описка или вычислительная ошибка. |
| | 2 балла | Ход решения верный. Получен верный ответ. |
| №3 | 0 баллов | Неверно найден угол. |
| | 1 балл | Ход решения верный, найден угол. Может быть допущена описка или вычислительная ошибка. |
| | 2 балла | Ход решения верный. Получен верный ответ. |
| №3 | 0 баллов | Неверно найдена сторона треугольника. |
| | 1 балл | Ход решения верный, найдена сторона треугольника. Может быть допущена описка или вычислительная ошибка. |
| | 2 балла | Ход решения верный. Получен верный ответ. |
Критерии оценивания:
7-8 баллов – «5» (отлично)
6-7 баллов – «4» (хорошо)
4-5 баллов «3» (удовлетворительно)
Менее 4 баллов- «2» (неудовлетворительно)
Контрольная работа № 1 по теме: «Четырехугольники»
Цель проверить усвоение: Определение четырехугольника. Параллелограмм и его свойства. Признаки параллелограмма. Прямоугольник, ромб, квадрат и их свойства.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: формирование систематических
знаний о плоских фигурах и их
свойствах, представлений о
простейших пространственных
телах; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
владение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений
К-1. Вариант 1.
1. В параллелограмме ABCD диагонали пересекаются в точке О. а) Докажите, что треугольник АОВ равен треугольнику COD. б) Известно, что АС =10 см, BD = 6 см, АВ = 5 см. Определите периметр треугольника АОВ.
2. Один из углов параллелограмма равен 45°. Высота параллелограмма, проведенная из вершины его тупого угла, равная 4 см, делит сторону параллелограмма на два равных отрезка. Периметр параллелограмма равен 27,4 см. Найдите: а) стороны параллелограмма; б) диагональ, проведенную из той же вершины, что и высота.
К-1. Вариант 2.
1. В четырехугольнике ABCD диагональ АС разбивает его на два равных треугольника ВАС и DCA. а) Докажите, что данный четырехугольник — параллелограмм, б) Известно, что угол ВАС равен 30°, а угол ВСА равен 40°. Определите углы параллелограмма.
2. Из вершины тупого угла ромба, равного 120°, проведена высота, которая отсекает от стороны отрезок 2 см.
а) Найдите периметр ромба и длину меньшей диагонали.
б) Докажите, что высота является биссектрисой угла, образованного диагональю и стороной ромба.
К-1. Вариант 3
1. В прямоугольнике ABCD диагонали пересекаются в точке О. а) Докажите, что треугольник АОВ равнобедренный. б) Определите периметр треугольника АОВ, если известно, что АВ = 4 см, BD = 5 см.
2. Из вершины прямоугольника опущен перпендикуляр на диагональ, который делит ее на два отрезка, меньший из которых равен 2 см. Перпендикуляр образует с меньшей стороной прямоугольника угол в 30°. а) Вычислите длину меньшей стороны прямоугольника и длины диагоналей, б) Докажите, что данный перпендикуляр является биссектрисой угла, образованного другой диагональю и меньшей стороной прямоугольника.
К-1. Вариант 4
1. В ромбе ABCD диагональ BD равна его стороне, а) Докажите, что треугольник ABD равносторонний, б) Известно, что ВО = 4 см (О — точка пересечения диагоналей). Найдите периметр ромба.
2. Периметр ромба равен 16 см; высота, проведенная из вершины тупого угла, делит сторону ромба пополам, а) Определите углы ромба, длину диагонали, проведенной из той же вершины, б) Докажите, что высота является биссектрисой угла, образованного данной диагональю и стороной ромба.
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ № 1

КОНТРОЛЬНАЯ РАБОТА № 2
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель проверить усвоение: Теорема Фалеса, средняя линия треугольника, средняя линия трапеции.
Цель: проверить уровень усвоения учащимися: Ряд натуральных чисел. Десятичная запись натуральных чисел. Сравнение натуральных чисел. Отрезок. Построение отрезка. Длина отрезка, построение заданной длины. Плоскость. Прямая. Луч.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями:ф ормирование систематических
знаний о плоских фигурах и их
свойствах, представлений о
простейших пространственных
телах; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
владение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений
К-2. Вариант 1.
1. В треугольнике АВС КМ — средняя линия (точки К и М лежат соответственно на сторонах АВ и ВС), а) Докажите, что периметр треугольника КВМ равен половине периметра треугольника АВС. б) Определите периметр треугольника КВМ, если треугольник АВС равносторонний со стороной 6 см.
2. ВА и BD — отрезки одной стороны угла В; ВС и BE — отрезки другой его стороны. Узнайте, параллельны ли прямые АС и DE, если BA:AD = 3:4, ВС = 1,2 м и BE = 2,8 м.
3. В треугольнике АВС проекции боковых сторон АС и ВС на основание АВ равны 15 см и 27 см, а большая боковая сторона равна 45 см. На какие части она делится (считая от вершины С) перпендикуляром к стороне АВ, проведенным из середины АВ?
К-2. Вариант 2.
1. Точки Р, М и К — середины сторон АВ, ВС и АС треугольника АВС. а) Докажите, что периметр треугольника РМК равен половине периметра треугольника АВС. б) Найдите периметр треугольника АВС, если РМ = 4 см, МК = 5 см, МР = 6 см.
2. Точка М делит отрезок АВ в отношении АМ:МВ = = 1:2. Найдите отношения АМ:АВ и МВ:АВ.
3. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке Р, AD = 10 см, средняя линия трапеции APCD равна 6 см. Определите периметр параллелограмма.
К-2. Вариант 3.
1. МК — средняя линия трапеции ABCD (точки М и К лежат соответственно на сторонах АВ и CD). Через точку К проведена прямая, параллельная стороне АВ и пересекающая сторону AD в точке Р. а) Докажите, что АМКР — параллелограмм. б) Найдите периметр параллелограмма АМКР, если АВ = 4 см, ВС = 5 см, AD=7 см.
2. Боковые стороны прямоугольной трапеции относятся как 1:2. Найдите наибольший угол трапеции.
3. В прямоугольнике ABCD АВ = 6 см, AD = 10 см, АК — биссектриса угла А (К принадлежит стороне ВС). Определите среднюю линию трапеции AKCD.
К-2. Вариант 4.
1. В равностороннем треугольнике АВС со стороной 8 см проведена средняя линия МК (точки М и К лежат соответственно на сторонах АВ и ВС), а) Докажите, что четырехугольник АМКС — равнобокая трапеция, б) Найдите периметр трапеции АМКС.
2. Три стороны трапеции равны а, углы при большем основании равны 60°. Определите периметр трапеции.
3. В параллелограмме ABCD AD = 20 см, АВ = BD, ВК — высота треугольника ABD. Определите среднюю линию трапеции KBCD.
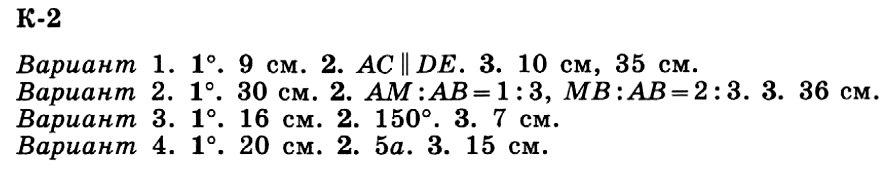
КОНТРОЛЬНАЯ РАБОТА № 3
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения учащимися: Синус, косинус и тангенс острого угла прямоугольного треугольника. Теорема Пифагора.
Неравенство треугольника.
Перпендикуляр и наклонная.
Соотношение между сторонами и углами в прямоугольном треугольнике.
Значения синуса, косинуса и тангенса некоторых углов.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями:
К-3. Вариант 1.
1. Катеты прямоугольного треугольника равны 8 см и 6 см. Определите гипотенузу.
2. В треугольнике АВС угол С равен 90°, угол А равен 30°, СВ = 3 см. Определите АС.
3. Катеты прямоугольного треугольника равны 8 см и 6 см. Найдите высоту, опущенную из вершины прямого угла.
К-3. Вариант 2
1. Стороны прямоугольника равны 12 см и 5 см. Найдите диагонали.
2. В окружность, радиус которой равен 17 см, вписан прямоугольник. Найдите стороны этого прямоугольника, если отношение их равно 15:8.
3. В прямоугольной трапеции разность оснований равна а. Наклонная боковая сторона трапеции равна b, а большая диагональ — с. Найдите основания трапеции.
К-3. Вариант 3
1. В равнобедренном треугольнике АВС высота BD равна 8 см, а основание АС равно 12 см. Найдите длину боковой стороны.
2. Периметр равнобедренного треугольника равен 24 дм, боковая сторона меньше основания на 1,5 дм. Найдите высоту этого треугольника.
3. Из одной точки проведены к кругу две касательные. Длина касательной равна 156 дм, а расстояние между точками касания равно 120 дм. Определите радиус круга.
К-3. Вариант 4
1. Диагонали ромба равны 10 см и 24 см. Найдите сторону ромба.
2. Высота равнобедренного треугольника равна 14 дм, основание относится к боковой стороне как 48:25. Найдите стороны этого треугольника.
3. Один из катетов прямоугольного треугольника равен 15 см, а проекция другого катета на гипотенузу равна 16 см. Найдите периметр треугольника.
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ
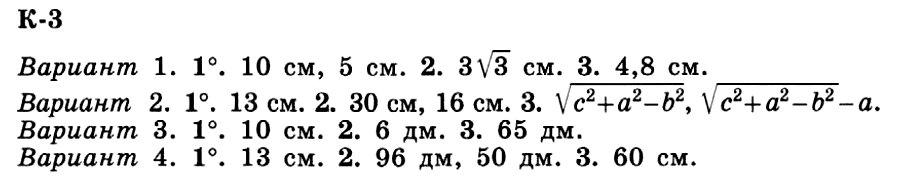
КОНТРОЛЬНАЯ РАБОТА № 4
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения учащимися: Ряд натуральных чисел. Десятичная запись натуральных чисел. Сравнение натуральных чисел. Отрезок. Построение отрезка. Длина отрезка, построение заданной длины. Плоскость. Прямая. Луч.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: формирование систематических
знаний о плоских фигурах и их
свойствах, представлений о
простейших пространственных
телах; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
владение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений
К-4. Вариант 1
1. В прямоугольном треугольнике АВС гипотенуза АВ равна 10 см, а катет АС равен 5 см. Найдите второй катет и острые углы треугольника.
2. Найдите острый угол между диагоналями прямоугольника со сторонами, равными 12 см и 8 см.
3. Докажите, что медиана треугольника меньше полусуммы сторон, из точки пересечения которых она проведена.
К-4. Вариант 2
1. В равнобедренном прямоугольном треугольнике гипотенуза равна 3√2 см. Найдите острые углы и катеты.
2. В прямоугольном треугольнике гипотенуза больше одного из катетов на 1 см, а второй катет равен 9 см. Вычислите угол, лежащий против меньшего катета.
3. Докажите, что сумма медиан треугольника меньше его периметра.
К-4. Вариант 3
1. В прямоугольном треугольнике даны катет 8 см и прилежащий к нему угол 54°. Найдите второй катет и гипотенузу.
2. В равнобедренном треугольнике угол при вершине равен α, высота, опущенная на боковую сторону, равна l. Найдите стороны треугольника.
3. Докажите, что сумма диагоналей трапеции больше суммы ее оснований.
К-4. Вариант 4
1. В прямоугольном треугольнике АВС гипотенуза АВ равна 8 см, а угол А равен 40°. Найдите катеты и второй острый угол.
2. Боковые стороны трапеции ABCD (BC||AD) при продолжении пересекаются под прямым углом. Найдите ВА, если ∠BAD = 28°, ВС = 8 см, AD=12 см.
3. Докажите, что каждая сторона треугольника меньше половины его периметр
скачать задания
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ

КОНТРОЛЬНАЯ РАБОТА № 5
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения Прямоугольная система координат на плоскости.
Координаты середины отрезка.
Расстояние между точками.
Уравнения прямой и окружности. Координаты точки пересечения прямых. График линейной функции.
Пересечение прямой с окружностью.
Синус, косинус и тангенс углов от 0° до 180°.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: овладение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
К-5 Вариант 1
1. Точки B (6; 0) и D(0; 8) являются концами диаметра окружности. Найдите: а) координаты центра окружности; б) длину радиуса окружности; в) запишите уравнение данной окружности.
2. Отрезок BD является диагональю прямоугольника ABCD, где А(0; 0), В (6; 0), В(0; 8). Найдите координаты вершины С и периметр прямоугольника.
К-5 Вариант 2
1. Прямая а задана уравнением 4х + 3у — 6 = 0. Найдите: а) координаты точек А и В пересечения прямой с осями координат (А и В лежат соответственно на осях х и у); б) длину АВ; в) постройте эту прямую.
2. Запишите уравнение прямой b, параллельной оси ординат и пересекающей прямую а, заданную уравнением 4x + 3y — 6 = 0, в точке С(-1,5; 4). Найдите периметр треугольника, ограниченного прямыми а и b и осью абсцисс.
К-5 Вариант 3
1. Точки А(-2; 4), В(-6; 12) и С(2; 8) являются вершинами параллелограмма ABCD. Найдите: а) координаты точки пересечения диагоналей; б) длины сторон параллелограмма; в) координаты его четвертой вершины.
2. Запишите уравнения прямых, на которых лежат диагонали параллелограмма ABCD из задания 1.
К-5 Вариант 4
1. Прямая а пересекает окружность в точках А (-7; 7) и В (-1; -1) и проходит через ее центр. Найдите: а) координаты центра окружности; б) длину радиуса окружности; в) запишите уравнения окружности и прямой а.
2. Отрезок АВ является диагональю прямоугольника ACBD, где С(1; 2), А(-7; 7) и В(-1; -1). Найдите координаты вершины D и периметр прямоугольника ACBD.
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ
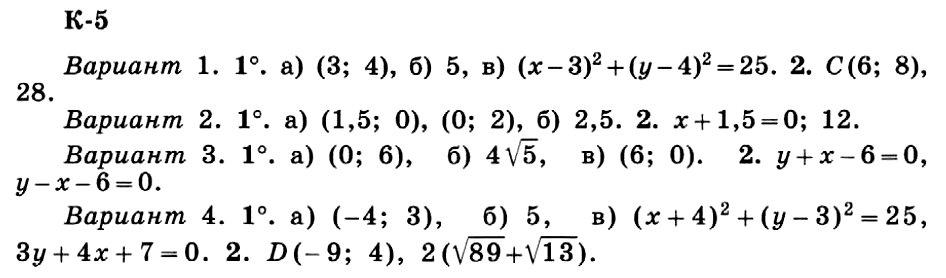
КОНТРОЛЬНАЯ РАБОТА № 5
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения учащимися: Движение и его свойства.
Симметрия относительно точки и прямой.
Поворот. Параллельный перенос и его свойства. Понятие о равенстве фигур.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: формирование систематических
знаний о плоских фигурах и их
свойствах, представлений о
простейших пространственных
телах; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
владение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений
КОНТРОЛЬНАЯ РАБОТА № 6
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
К-6 Вариант 1
Дан отрезок АВ, где А(3; -1), В(1; -2).
1°. Постройте отрезок А1В1, симметричный отрезку АВ относительно начала координат, и укажите координаты точек А1 и B1.
2°. Существует ли параллельный перенос, при котором точка В переходит в точку С, а точка А — в точку B1?
3. При условии, что существует параллельный перенос, задайте его формулами.
4. Докажите, что полупрямые АВ и А1В1 противоположно направлены.
5. Докажите, что четырехугольник АВА1В1 — параллелограмм.
К-6 Вариант 2
Дан треугольник АВС, где А( 1; 4), В(3; 2), С(-1; 2).
1°. Постройте точку А1, симметричную точке А относительно прямой СВ, и укажите ее координаты.
2°. Существует ли параллельный перенос, при котором точка А переходит в точку С, точка В — в точку А1?
3. При условии, что параллельный перенос существует, задайте его формулами.
4. Докажите, что полупрямые АВ и СА1 одинаково направлены.
5. Докажите, что полученная фигура — квадрат.
К-6 Вариант 3
Дан отрезок CD, где С (-4; 1), П(-1; 1).
1°. Постройте отрезок C1D1, симметричный отрезку CD относительно оси х, и укажите координаты точек С, и D1.
2°. Существует ли параллельный перенос, при котором точка С переходит в точку Сх, точка D — в точку D1?
3. При условии, что параллельный перенос существует, задайте его формулами.
4. Докажите, что полупрямые CD и C1D1 одинаково направлены.
5. Докажите, что четырехугольник CDD1C1 — прямоугольник.
К-6 Вариант 4
Дан треугольник АВС, где А(-1; 1), В(-3; -2), С(-1; -5).
1°. Постройте точку В1, симметричную точке В относительно прямой АС, и укажите координаты точки В1.
2°. Существует ли параллельный перенос, при котором точка В переходит в точку А, точка С — в точку В1?
3. При условии, что параллельный перенос существует, задайте его формулами.
4. Докажите, что лучи АВ и СВ1 противоположно направлены.
5. Докажите, что четырехугольник АВСВ1 — ромб.
скачать задания
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ
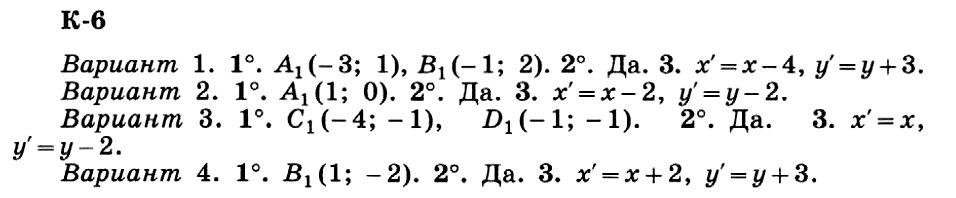
КОНТРОЛЬНАЯ РАБОТА № 7
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения учащимися: Вектор. Абсолютная величина и направление вектора. Равенство векторов. Координаты вектора. Сложение векторов и его свойства. Умножение вектора на число. Коллинеарные векторы. Скалярное произведение векторов. Угол между векторами. Проекция на ось. Разложение вектора по координатным осям.
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: овладение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач

ТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ

ТОГОВАЯ (ГОДОВАЯ) КОНТРОЛЬНАЯ РАБОТА
(ГЕОМЕТРИЯ 8 КЛАСС, УМК ПОГОРЕЛОВ)
Цель: проверить уровень усвоения учащимися: содержание геометрии 8 класс
Требования к результатам освоения основной
образовательной программы основного общего
образования, проверяемые заданиями: формирование систематических
знаний о плоских фигурах и их
свойствах, представлений о
простейших пространственных
телах; развитие умений
моделирования реальных
ситуаций на языке геометрии,
исследования построенной
модели с использованием
геометрических понятий и
теорем, аппарата алгебры,
решения геометрических и
практических задач
владение геометрическим
языком; развитие умения
использовать его для описания
предметов окружающего мира;
развитие пространственных
представлений, изобразительных
умений, навыков геометрических
построений
К-8 Вариант 1
1. Диагонали ромба равны 1,6 см и 3 см. Чему равна сторона данного ромба?
2. Катет, противолежащий углу в 60° данного прямоугольного треугольника, равен 3 см. Найдите гипотенузу, второй катет и острый угол этого треугольника.
3. Вершинами четырехугольника ABCD являются точки А(0; 0), В(1; 2), С(2; 0) и D(1; -2). Докажите, что данный четырехугольник является ромбом.
К-8 Вариант 2
1. Стороны прямоугольника равны 1,6 дм и 3 дм. Чему равна диагональ данного прямоугольника?
2. Катет, прилежащий к углу в 30° данного прямоугольного треугольника, равен 9 дм. Найдите гипотенузу, второй острый угол и катет этого треугольника.
3. Вершинами четырехугольника PQRS являются точки Р(0; 0), Q(1; 2), R(5; 0) и S(4; -2). Докажите, что данный четырехугольник является прямоугольником.
К-8 Вариант 3
1. У равнобокой трапеции боковая сторона и меньшее основание равны 5 см, расстояние между основаниями равно 1,4 см. Найдите большее основание данной трапеции.
2. Один из углов трапеции равен 30°, а боковые стороны при их продолжении пересекаются под прямым углом. Найдите меньшую боковую сторону трапеции, если ее средняя линия равна 5 см, а меньшее основание — 4 см.
3. Известны координаты первых трех вершин параллелограмма ABCD: А(5; -4), В(2; -3) и С(-1; -4). Докажите, что данный параллелограмм является ромбом, не находя координат вершины D. Является ли данный параллелограмм квадратом? Ответ объясните.
К-8 Вариант 4
1. У равнобокой трапеции боковая сторона равна 3 дм, ее большее основание, равное 7 дм, находится на расстоянии 1,8 дм от меньшего основания. Найдите меньшее основание данной трапеции.
2. У равнобокой трапеции боковая сторона и меньшее основание равны 15 дм. Диагонали трапеции образуют между собой острый угол в 60°. Найдите большее основание данной трапеции.
3. Известны координаты первых трех вершин параллелограмма PQRS: Р(4; 7), Q(-2; 3) и R(-5; 11). Докажите, что данный параллелограмм является прямоугольником, не находя координат вершины S. Является ли данный параллелограмм квадратом? Почему?
скачать задания
ОТВЕТЫ НА КОНТРОЛЬНУЮ РАБОТУ






 )Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.