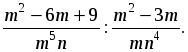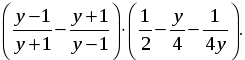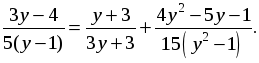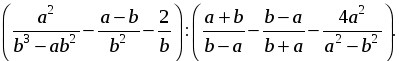Контрольная работа №1 по теме «Алгебраические дроби».
Цели: проверить знания и умения учащихся по теме «Алгебраические дроби».
В а р и а н т 1
1) Сократить данную дробь 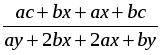 и найти ее числовое значение при заданных переменных
и найти ее числовое значение при заданных переменных 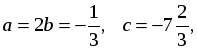 x = 3, y = –4.
x = 3, y = –4.
2) Выполнить действия:
а) 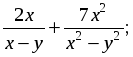 б)
б) 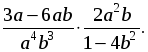
3) Упростить выражение: 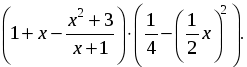
4) Решить уравнения:
а) 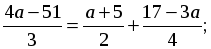 б)
б) 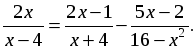
5*) Упростить выражение:
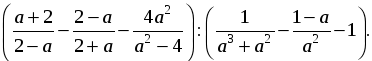
В а р и а н т 2
1) Сократить данную дробь 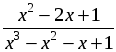 и найти ее числовое значение при заданной переменной
и найти ее числовое значение при заданной переменной 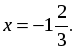
2) Выполнить действия:
а) 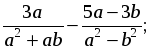 б)
б) 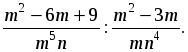
3) Упростить выражение: 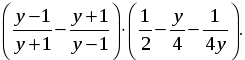
4) Решить уравнения:
а) 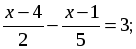 б)
б) 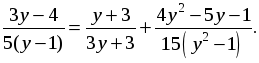
5*) Упростить выражение:
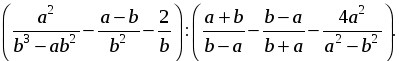
Контрольная работа №2 по теме «Функция 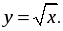
Цели: проверить знания и умения учащихся по теме «Функция 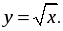 Свойства квадратного корня».
Свойства квадратного корня».
В а р и а н т 1
1) Найдите значение данных выражений:
а) 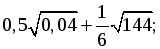 б)
б) 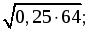
в) 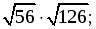 г)
г) 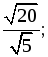 д)
д) 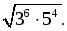
2) Решить уравнение 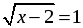 графическим способом.
графическим способом.
3) Упростить:
а) 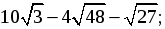 б)
б)  в)
в) 
4) Освободите дробь от знака корня в знаменателе:
а)  б)
б) 
5*) Упростить выражение:
В а р и а н т 2
1) Найдите значение данных выражений:
а) б) 
в)  г)
г)  д)
д) 
2) Решить уравнение  графическим способом.
графическим способом.
3) Упростить:
а) б)  в)
в) 
4) Освободите дробь от знака корня в знаменателе:
а)  б)
б) 
5*) Упростить выражение:
Контрольная работа №3 по теме «Квадратичная функция. Функция вида ».
».
Цели: проверить знания учеников по теме «Квадратичная функция. Функция вида  ».
».
В а р и а н т 1
1) Построить график функции  и описать ее свойства.
и описать ее свойства.
2) Решить систему уравнений графическим способом
3) Дана функция y = f(x), где
Вычислите f(2), f(4). Постройте график данной функции.
4) Решить графически уравнение –x2 – 2x + 3 = 0.
5*) При каком значении p уравнение x2 – 4x + 5 = p имеет один корень?
В а р и а н т 2
1) Построить график функции и описать ее свойства.
2) Решить систему уравнений графическим способом
3) Дана функция y = f(x), где
Вычислите f(–1), f(2). Постройте график данной функции.
4) Решить графически уравнение x2 + 4x + 3 = 0.
5*) При каком значении p уравнение x2 + 4x – 1 = p не имеет корней?
Контрольная работа № 4 по теме «Квадратные уравнения».
Цели: проверить знания и умения учеников по теме «Квадратные уравнения».
В а р и а н т 1
1) Решить уравнения:
а) 2x2 + 7x – 9 = 0; б) (6y – 4)(y – 4) = 7(y2 – 4y – 12);
в) г) x4 – 10x2 + 9 = 0.
2) В уравнении x2 + kx + 56 = 0 один из его корней равен –8. Найдите коэффициент k для данного уравнения.
3) Решить иррациональное уравнение 
4) Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шел 18 км по озеру. Какова собственная скорость катера, если скорость течения реки 3 км/ч?
5*) Не решая уравнения 2x2 – 3x + 6 = 0, найти значение выражения 
В а р и а н т 2
1) Решить уравнения:
а) 7x2 – 9x + 2 = 0; б) (y – 2)2 + 4y = 53;
в) г) x4 – x2 – 12 = 0.
2) В уравнении x2 – 7x + k = 0 один из его корней равен 11. Найдите коэффициент k для данного уравнения.
3) Решить иррациональное уравнение 
4) Катер прошел 15 км против течения реки и 6 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шел 22 км по озеру. Какова собственная скорость катера, если скорость течения реки 2 км/ч?
5*) Не решая уравнения 2x2 + 8x – 1 = 0, найти значение выражения 
Контрольная работа № 5 по теме «Неравенства».
Цели: проверить знания и умения учащихся по теме «Неравенства».
В а р и а н т 1
1) Сравнить числа:
а)  и
и  б)
б)  и
и 
2) Решить неравенства:
а) 2(x – 1) 5(3 + x) + 1; б) 2x2 – 3x ≤ 2;
в)
3) Построить график функции
Перечислите свойства данной функции.
4) При каких значениях переменной x имеет смысл выражение:
а)  б)
б) 
5*) Найдите область определения данной функции:
В а р и а н т 2
1) Сравнить числа:
а)  и
и  б)
б)  и
и 
2) Решить неравенства:
а) 4(x – 1) – (9x – 5) ≥ 3; б) x2 x;
в)
3) Построить график функции
Перечислите свойства данной функции.
4) При каких значениях переменной x имеет смысл выражение:
а)  б)
б) 
5*) Найдите область определения данной функции:
Итоговая контрольная работа №6 за курс 8 класса
Цели: проверить знания и умения учащихся по курсу 8 класса.
В а р и а н т 1
1) Упростите выражение
2) Решить уравнения:
а) 3x2 + 13x – 10 = 0; б) x4 – 17x2 + 16 = 0;
в)  г)
г) 
3) Решить неравенства:
а) 18 – 8(x – 2) x; б) 2x2 + 5x – 3 0; в)
4) Построить график функции
Записать свойства данной функции.
5) От турбазы до станции турист доехал на велосипеде за 3 часа. Пешком он смог бы пройти это расстояние за 7 часов. Известно, что пешком он идет со скоростью на 8 км/ч меньшей, чем едет на велосипеде. С какой скоростью ехал турист?
В а р и а н т 2
1) Упростите выражение
2) Решить уравнения:
а) 5x2 – 2x – 3 = 0; б) x4 + 2x2 – 3 = 0;
в) г) 
3) Решить неравенства:
а) 3(1 – x) ≤ 2; б) –x2 + 3x – 2
4) Построить график функции
Записать свойства данной функции.
5) Два велосипедист отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км, и встретились через 2 ч. Определите скорость каждого велосипедиста, если у одного она на 2 км/ч больше, чем у другого.





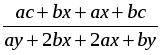 и найти ее числовое значение при заданных переменных
и найти ее числовое значение при заданных переменных 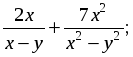 б)
б) 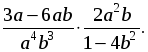
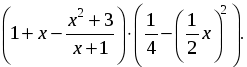
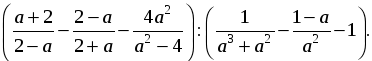
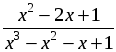 и найти ее числовое значение при заданной переменной
и найти ее числовое значение при заданной переменной